欢迎访问《控制理论与应用》期刊网站！

带有输入饱和的非线性全驱系统级联预测控制

doi: 10.7641/CTA.2025.40297

王秀博^1,2 ，段广仁^2,3

1. 东北大学秦皇岛分校控制工程学院, 河北秦皇岛 066004

2. 哈尔滨工业大学控制理论与制导技术研究中心, 黑龙江哈尔滨 150001

3. 南方科技大学深圳市控制理论与智能系统重点实验室, 广东深圳 518055

基金项目: 国家自然科学基金委基础科学中心项目(62188101), 河北省自然科学基金项目(F2025501004), 中央高校基本科研业务费专项资金项目(Z2025– 041)资助.

详细信息

作者简介

王秀博博士研究生,目前研究方向为全驱系统方法、预测控制、飞行器控制和航天器控制,E-mail: xiubowang@outlook.com;

段广仁中国科学院院士,国家杰出青年基金获得者,长江学者特聘教授,目前研究方向为全驱系统方法、控制系统的参数化设计、鲁棒控制、广义系统、航天器制导与控制,E-mail: g.r.duan@hit.edu.cn.

通信作者

王秀博，E-mail: xiubowang@outlook.com.

Cascade predictive control for nonlinear fully-actuated systems with input saturation

WANG Xiu-bo^1,2 ， DUAN Guang-ren^2,3

1. School of Control Engineering, Northeastern University at Qinhuangdao, Qinhuangdao Hebei 066004 , China

2. Center for Control Theory and Guidance Technology, Harbin Institute of Technology, Harbin Heilongjiang 150001 , China

3. Shenzhen Key Laboratory of Control Theory and Intelligent Systems, Southern University of Science and Technology, Shenzhen Guangdong 518055 , China

Funds: Supported by the Science Center Program of the National Natural Science Foundation of China (62188101), the Natural Science Foundation of Hebei Province (F2025501004) and the Fundamental Research Funds for the Central Universities (Z2025–041).

摘要

基于全驱系统方法的预测控制通过非线性输入变换, 将原始输入映射为期望的线性闭环系统输入, 进而构造分散式线性预测模型, 降低了优化问题求解的复杂度. 然而, 当系统具有输入饱和约束时, 此类输入变换为期望的预测模型引入强非线性的约束问题. 为此, 本文提出了一种级联预测控制方法, 设计了双层优化结构的级联预测控制器: 第1层优化结合上一时刻的预测输入序列, 优化预测时域内输入变换后的线性边界; 第2层优化则基于重新定义的线性约束, 求解带有松弛因子的分散式线性优化问题. 该方法有效避免了因输入变换引发的非线性约束问题, 降低优化复杂度, 并提高非线性优化问题的可解性, 同时保证闭环系统的稳定性. 最后, 通过对全驱航天器姿态系统和欠驱转动平移驱动系统的仿真, 验证了所提算法的有效性.

关键词

非线性系统 / 预测控制 / 全驱系统方法 / 级联优化 / 输入饱和

Abstract

Predictive control based on fully actuated system (FAS) approaches employs nonlinear input transformations to map the original inputs into the desired linear closed-loop system inputs. This enables the construction of distributed linear predictive models, effectively reducing the complexity of solving the optimization problem. However, when the system owns input saturation, such input transformations introduce highly nonlinear constraint issues to the desired predictive model. To address this, this paper proposes a cascaded predictive control method and designs a cascaded predictive controller with a two-layer optimization structure. In the first layer of optimization, the predictive input sequence from the previous instant is used to optimize the linear boundaries of the transformed inputs within the predictive horizon. In the second layer of optimization, based on the newly defined linear constraints, a series of distributed linear optimization problems with slack factors are solved. This cascaded predictive method effectively avoids the nonlinear constraint issues caused by input transformations, reduces optimization complexity, improves the solvability of nonlinear optimization problems, and ensures the stability of the closed-loop system. Finally, the effectiveness of the proposed algorithm is verified through simulations on fully-actuated spacecraft attitude system and the under-actuated rotational translational actuator system.

Keywords

nonlinear systems / predictive control / fully actuated system approaches / cascade optimization / input saturation

1 引言 2 问题描述 3 主要结果 3.1 稳定性分析 4 案例 4.1 航天器姿态控制系统 4.2 航天器消旋系统 5 结论

1 引言

预测控制起源于20世纪60年代，因其显式处理多变量约束的优势已经迅速发展成为控制理论和工程应用中极为重要的一部分 ^[1-2] . 预测控制广泛应用于化工和石油炼制、能源管理和电力、汽车工业、航空航天、机器人技术、水处理和环境工程、农业、医疗设备和健康监护等领域 ^[3-7] .

当前非线性预测控制主要基于一阶状态空间方法，可分为3类: 基于线性化方法的预测控制通过对非线性系统线性化建立预测模型，但存在局部线性化误差和适配性问题 ^[8]; 基于人工智能的预测模型逼近方法利用神经网络和模糊控制等技术简化了模型复杂度，但忽略了物理属性，可能导致模型偏差 ^[9]; 非近似的非线性模型预测方法提供精确预测模型，但因非线性优化计算负担过高限制了实时控制效率，且随着控制系统模型复杂度的提升，预测控制中优化问题的求解变得困难 ^[10] . 即使在无约束条件下，通过变量增广得到的一阶状态空间预测模型也极其复杂，随之导致优化问题的求解变得更加困难. 通常，这需要投入大量的计算资源和时间来寻找最优的预测控制序列. 特别是在高维多变量系统或有限预测时域较长的情况下，优化问题计算复杂度会显著增加 ^[11] . 若进一步考虑系统的约束条件，不仅优化问题的求解时间更长，控制预测序列的求解可能无法满足实时控制要求，导致系统性能下降或者不稳定，甚至出现优化解不存在的情况 ^[12] . 此外，带有输入饱和约束的非线性预测控制问题通常会转化为一个难以求解的非凸优化问题.

非线性预测控制问题求解的瓶颈在于系统模型的复杂性. 通过变量增广将原始非线性系统转换为一阶状态空间，复杂的非线性特征传递到预测模型和滚动优化问题中 ^[13] . 然而，状态空间模型并不是用来描述动态控制系统的唯一或原始形式. 在许多实际物理系统中，根据牛顿定律、动量定理、拉格朗日方程、基尔霍夫定律等物理定律建立的系统模型通常是二阶的，或被复合为高阶的或混合阶的 ^[14] . 在进行控制系统设计时，人们通常习惯性的将这些物理模型通过变量增广转换为一阶状态空间模型. 虽然状态空间方法对线性系统理论是完备的，但其在处理非线性系统的约束和可控性问题上具有明显的局限性 ^[15] .

不同于一阶状态空间方法，全驱系统方法在控制系统的分析和设计中具有巨大的优势和潜力，可以有效地降低控制设计中的复杂度，进而获得更为完备、简单、通用的控制律表达式 ^[14，16] . 因此，全驱系统方法的关键步骤是为所考虑的动力系统推导全驱系统模型. 一旦获得全驱系统模型，利用系统的全驱特性可直接设计稳定控制器. 在现实的物理世界中，根据基本物理法则（如牛顿运动定律、动量守恒定律和能量守恒定律等），可以推导出广义的全驱系统模型，并且高度自动化的系统模型通常是全驱系统特性的典型体现. 此外，全驱系统方法的适用系统不限于传统的全驱系统. 在处理欠驱系统时，现有文献克服了控制输入维度受限的问题，通过诸如状态消元升阶或寻找同胚变换的方法，能够将欠驱系统转化为全驱系统、包含自治子系统的复合全驱系统或亚全驱系统，这在系统模型层面揭示了系统的可控性和内在的动态特性，并为基于全驱系统控制理论实现预期控制目标提供了依据 ^[17] . 在处理非完整系统时，针对典型的非完整系统和以积分链形式存在的广义非完整系统，基于全驱系统方法的亚全驱或非连续控制策略实现了对这些系统的有效控制 ^[18] .

与传统的预测控制方法相比，全驱系统理论集成到预测控制中，大大降低了优化问题的复杂性. 但值得注意的是，在现有基于全驱系统方法预测控制文献 ^{[12-13，19-20]} 中，全驱预测控制器的通常表征为: u（k）=−B⁻¹（·）（f（·）− v（k）），其中: B（·）和f（·）是与系统相关的非线性函数，v（k）是预测控制器. 可以看出，系统输入u到预测跟踪控制器v存在非线性输入变换. 当全驱系统存在线性输入约束时，在预测时域内经过此输入变换为期望的预测模型:

x （ k + i + 1 ） = A^{i} x （ k ） + \sum_{j = 0}^{i - 1} A^{j} B v （ k + j ）

引入了强非线性输入约束，进而解耦的线性优化问题将重新回归为耦合的非线性优化问题. 因此，本文针对具有输入约束的非线性混合阶全驱系统，提出了一种基于级联优化的预测控制方法，在对参考信号进行跟踪的同时，保证系统输入满足系统输入约束条件，并通过对全驱航天器姿态系统和欠驱旋转平移驱动（rotational translational actuator，RTAC）系统的仿真，验证了所提算法的有效性. 具体地，本文的主要贡献概括为以下两点:

1）级联优化: 设计一个采用双层优化的预测级联控制器. 在第1层优化中，结合上一时刻的预测跟踪输入序列，优化求解预测时域内经输入变换后的新输入约束线性边界. 在第2层优化中，利用新定义的线性约束，优化跟踪预测性能指标，从而有效避免因非线性输入变换而引入的非线性约束;

2）状态松弛: 设计包含未知状态松弛因子的跟踪预测指标，通过优化求解预测跟踪序列和松弛因子，确保输入和状态约束同时存在的情况下优化问题的可解性，并同时确保闭环系统的稳定性.

为便于阅读，本文采用以下符号:

R

ⁿ表示n维实向量空间，N表示整数空间，

R

^m^×ⁿ表示m × n维实矩阵，A⁻¹和A^T表示矩阵A的逆矩阵和转置矩阵，I_n表示n 阶单位矩阵. 对于向量

x \in R^{n} ， i ⩽ j \in N ， x_{i} \in R^{n} ， i ⩽ j \in N ，

定义如下符号:

x_{i \sim j} = {[\begin{matrix} x_{i}^{T} x_{i + 1}^{T} \dots x_{j}^{T} \end{matrix}]}^{T},

x_{i \sim j}^{(0 \sim n)} = {[\begin{matrix} {(x_{i}^{(0 \sim n)})}^{T} {(x_{i + 1}^{(0 \sim n)})}^{T} \dots {(x_{j}^{(0 \sim n)})}^{T} \end{matrix}]}^{T},

x^{⌊ 0 \sim n ⌋} (k) = [\begin{matrix} x (k) \\ x (k + 1) \\ ⋮ \\ x (k + n) \end{matrix}],

x_{i \sim j}^{⌊ 0 \sim n ⌋} (k) = [\begin{matrix} x_{i}^{⌊ 0 \sim n ⌋} (k) \\ x_{i + 1}^{⌊ 0 \sim n ⌋} (k) \\ ⋮ \\ x_{j}^{⌊ 0 \sim n ⌋} (k) \end{matrix}] .

2 问题描述

考虑下述非线性混合阶全驱系统 ^[15] :

[\begin{matrix} x_{1}^{⌊μ_{1} - 1⌋} (k + 1) \\ x_{2}^{⌊μ_{2} - 1⌋} (k + 1) \\ ⋮ \\ x_{η}^{⌊μ_{η} - 1⌋} (k + 1) \end{matrix}] = [\begin{matrix} f_{1} ({x_{p}^{⌊0 \sim μ_{p} - 1⌋} (k)|}_{p = 1 \sim η}) \\ f_{2} ({x_{p}^{⌊0 \sim μ_{p} - 1⌋} (k)|}_{p = 1 \sim η}) \\ ⋮ \\ f_{η} ({x_{p}^{⌊0 \sim μ_{p} - 1⌋} (k)|}_{p = 1 \sim η}) \end{matrix}] + B (\cdot) u (k),

(1)

其中:

x_{p} \in R^{r_{p}} ， p = 1，2 ， \dots ， η

是系统的状态向量;

f_{p} （ \cdot ） \in R^{r_{p}} ， p = 1，2 ， \dots ， η

为非线性向量函数，满足

f_{p} （ 0 ） = 0 .

令

r = \sum_{p = 1}^{η} r_{p} ， χ = \sum_{p = 1}^{η} r_{p} μ_{p} ， μ_{p} ， r_{p} ， p = 1，2 ， \dots ， η

是一系列正整数，

u \in R^{r}

是输入向量，B（·）=

B ({x_{p}^{⌊0 \sim μ_{p} - 1⌋} （ k ）|}_{p = 1 \sim η}) \in R^{r \times r}

是输入配置矩阵函数. 系统的状态约束为

x_{p}^{⌊0 \sim μ_{p} - 1⌋} (k) \in X_{p}, p = 1,2, \dots, η, k ⩾ 0,

(2)

其中:

X_{p} = \{z_{p} \in R^{μ_{p} r_{p}} ∣ G_{p} z_{p} ⩽ g_{p}\} ， G_{p}

和g_p是具有适当维度的矩阵和向量. 系统的输入约束为

u (k) \in U \subseteq R^{r}, k ⩾ 0,

(3)

其中

U = \{u \in R^{r} ∣ u_{m i n} ⩽ u ⩽ u_{m a x}\} .

系统的全状态向量约束记为

{x_{p}^{⌊0 \sim μ_{p} - 1⌋} (k)|}_{p = 1 \sim η} \in X \subseteq R^{X}

其中

X = \{z_{1 \sim η} \in R^{χ} ∣ z_{p} \in X_{p} ， p = 1，2 ， \dots ， η\} .

本文对系统（1）所需的全驱条件、状态以及参考跟踪信号

{γ_{p}^{⌊0 \sim μ_{p} - 1⌋} （ k ）|}_{p = 1 \sim η}

做下述假设 ^[13] :

假设 1 det B（X）≠ 0或∞，∀k >0，X ∈ X .

假设 2

x_{p}^{⌊0 \sim μ_{p} - 1⌋} （ k ）

，p = 1，2，· · ·，η已知.

假设 3 跟踪参考信号

γ_{p}^{⌊0 \sim μ_{p} - 1⌋} （ k + i ） ， i = 0

，1，· · ·，N，p = 1，2，· · ·，η已知.

在前期工作 ^[12-13] 中，全驱预测控制器的形式往往设计如下:

\{\begin{matrix} u (k) = B^{- 1} (\cdot) (v_{1 \sim η} (k) - f_{1 \sim η} (\cdot)), \\ v_{p} (k) = V_{e_{p}} (k) + γ_{p}^{⌊μ_{p}⌋} (k) . \end{matrix}

(4)

定义跟踪误差系统的状态和输入为

\{\begin{matrix} e_{p}^{⌊0 \sim μ_{p} - 1⌋} (k) = x_{p}^{⌊0 \sim μ_{p} - 1⌋} (k) - γ_{p}^{⌊0 \sim μ_{p} - 1⌋} (k), \\ V_{e_{p}} (k) = v_{p} (k) - γ_{p}^{⌊μ_{p}⌋} (k), \end{matrix}

滚动优化指标设为

\begin{matrix} J (k) = \\ \frac{1}{2} \sum_{i = 0}^{N - 1} ({‖{e_{p}^{⌊0 \sim μ_{p} - 1⌋} (k + i ∣ k)|}_{p = 1 \sim η}‖}_{\bar{Q}}^{2} + \\ {‖{V_{e_{p}} (k + i ∣ k)|}_{p = 1 \sim η}‖}_{\bar{R}}^{2}) + \\ \frac{1}{2} {‖{e_{p}^{⌊0 \sim μ_{p} - 1⌋} (k + N ∣ k)|}_{p = 1 \sim η}‖}_{\bar{F}}^{2}, \end{matrix}

(5)

且

\{\begin{matrix} \bar{Q} = d i a g \{Q_{p}, p = 1, 2, \dots, η\}, Q_{p} ⩾ 0, \\ \bar{R} = d i a g \{R_{p}, p = 1, 2, \dots, η\}, R_{p} > 0, \\ \bar{F} = d i a g \{F_{p}, p = 1, 2, \dots, η\}, F_{p} ⩾ 0, \end{matrix}

其中Q_p，R_p，F_p，p = 1，2，· · ·，η是预测权重矩阵.

值得注意的是，式（4）的第1子式可视为原始u（k）到新输入v_1∼_η（k）的非线性输入变换. 在预测时域内，线性时不变输入约束u（k + i|k）∈ U转化为时变非线性约束v_1∼_η（k + i|k）∈ V_k₊_i_|_k，

V_{k + i ∣ k} = \{V (k + i ∣ k) \in R^{r} ∣ \begin{matrix} ι (k + i ∣ k) \in U \\ X (k + i ∣ k) \in X \end{matrix}\},

其中:

\begin{matrix} ι (k + i ∣ k) = B^{- 1} (X (k + i ∣ k)) V (k + i ∣ k) - \\ B^{- 1} (X (k + i ∣ k)) f_{1 \sim η} (X (k + i ∣ k)), \end{matrix}

X (k + i ∣ k) = {x_{p}^{⌊0 \sim μ_{p} - 1⌋} (k + i ∣ k)|}_{p = 1 \sim η} .

当i= 0时，X_p（k）已知，V_k为线性约束空间. 当1≤ i≤N − 1时，X（k + i|k）未知，约束空间V_k₊_i_|_k 与状态约束X（k + i|k）∈ X和输入约束u（k）∈ U同时相关，那么对应预测控制中的优化问题将由带有线性约束的非线性优化问题转化为下述带有混合非线性约束的非线性优化问题:

\underset{\begin{matrix} v_{1} \sim η (k + i), i = 0, 1, \dots, N - 1 \end{matrix}}{m i n} J (k),

s.t. X (k + i ∣ k) \in X,

v_{1 \sim η} (k + i ∣ k) \in V_{k + i ∣ k} .

这意味着，非线性混合全驱系统（1）预测控制中的优化问题复杂度进一步提升，优化求解所需时间更长，控制系统的实时性和稳定性都很难保证，甚至连解的存在性都无法保证.

问题 1 在假设1–3的条件下，考虑具有状态约束（2）和输入约束（3）的非线性混合阶全驱系统（1）的预测跟踪问题. 设计结合双层优化策略的全驱预测级联控制器，解决经过非线性输入转换（4）引入的非线性约束问题. 在优化的首层，通过一步线性优化求解跟踪误差系统输入约束边界，在二层优化中，利用这些重新定义的边界来优化跟踪性能指标，进而组成一种全驱预测复合控制律，使得

1）刻画系统性能的预测指标最小;

2）系统状态渐近跟踪参考信号;

3）控制器解的存在性以及系统的稳定性得以保证.

3 主要结果

如图1所示，全驱预测控制器由非线性补偿部分、预测跟踪控制器部分，以及参考补偿部分组成，其中预测跟踪控制器通过级联优化确定. 算法实现包括以下3个步骤，分述如下:

步骤 1 分散式预测模型的表征.

将控制器（4）代入系统（1），跟踪误差系统可解耦为

e_{p}^{⌊0 \sim μ_{p} - 1⌋} (k + 1) = A_{p} e_{p}^{⌊0 \sim μ_{p} - 1⌋} (k) + B_{p} V_{e_{p}} (k),

p = 1,2, \dots, η

(6)

其中:

A_{p} = [\begin{matrix} 0 I_{r_{p}} \\ ⋱ \\ I_{r_{p}} \\ 0 & 0 & \dots & 0 \end{matrix}], B_{p} = [\begin{matrix} 0 \\ ⋮ \\ 0 \\ I_{r_{p}} \end{matrix}] .

(7)

当k >1时，上一时刻的预测跟踪误差输入序列记为

V_{e_{p}} (k - 1 ∣ k - 1) = [\begin{matrix} V_{e_{p}} (k - 1 ∣ k - 1) \\ V_{e_{p}} (k ∣ k - 1) \\ ⋮ \\ V_{e_{p}} (k + N - 1 ∣ k - 1) \end{matrix}],

(8)

其中，第1项

V_{e_{p}}

（k − 1|k − 1）=

V_{e_{p}}

（k − 1）用于计算 u（k − 1），剩余项作为当前时刻的跟踪误差系统的预测控制输入序列，记为

V_{e_{p}} (k ∣ k - 1) = [\begin{matrix} V_{e_{p}} (k ∣ k - 1) \\ V_{e_{p}} (k + 1 ∣ k - 1) \\ ⋮ \\ V_{e_{p}} (k + N - 1 ∣ k - 1) \\ V_{e_{p}} (k + N ∣ k - 1) \end{matrix}] .

(9)

具体地，结合上述当前时刻的预测误差系统控制输入序列（9）和解耦的跟踪误差系统（6），预测的误差状态

e_{p}^{⌊0 \sim μ_{p} - 1⌋} （ k + i ∣ k ） ， i = 0，1 ， \dots ， N

表示为

e_{p}^{⌊0 \sim μ_{p} - 1⌋} (k + i ∣ k) = \{\begin{matrix} A_{p}^{i} e_{p}^{⌊0 \sim μ_{p} - 1⌋} (k) + \\ \sum_{j = 1}^{i} A_{p}^{i - j} B_{p} V_{e_{p}} (k + j - 1 ∣ k), k = 0, \\ A_{p}^{i} e_{p}^{⌊0 \sim μ_{p} - 1⌋} (k) + \\ \sum_{j = 1}^{i} A_{p}^{i - j} B_{p} V_{e_{p}} (k + j - 1 ∣ k - 1), k ⩾ 1, \end{matrix}

(10)

其中跟踪误差

e_{p}^{⌊0 \sim μ_{p} - 1⌋} （ k ）

是已知的. 当k = 0时，输入序列

V_{e_{p}}

（k + j − 1|k），j = 1，2，· · ·，i为待求解; 当 k>1时，

V_{e_{p}}

（k + j − 1|k − 1），j = 1，2，· · ·，i为已知项.

注 1 估计的误差预测输入序列向量（9）最后一项

V_{e_{p}}

（k + N|k − 1）的值是任意的，可将其视为零（该项并未参与跟踪误差状态的预测，见式（10），进而不影响后续优化问题的求解）.

图1全驱系统级联预测控制系统框图

Fig.1The block diagram of cascaded predictive control for FASs

步骤 2 新输入约束上、下界优化求解.

根据式（4）的第1子式，有

v_{1 \sim η} (k) = h (X (k), u (k)),

h（X（k），u（k））= f_1∼_η（X（k））+B（X（k））u（k）. 为简便起见，记作h（X（k），u（k））= h（·，·，k），且下式成立: v_1∼_η（k+i|k）= h（·，·，k+i|k），i = 0，1，· · ·，N −1，其中

x_{p}^{⌊0 \sim μ_{p} - 1⌋} (k + i ∣ k) = e_{p}^{⌊0 \sim μ_{p} - 1⌋} (k + i ∣ k) + γ_{p}^{⌊0 \sim μ_{p} - 1⌋} (k + i),

(11)

预测跟踪误差

e_{p}^{⌊0 \sim μ_{p} - 1⌋} （ k + i ∣ k ）

由式（10）给出.

下面分别讨论k = 0和k >1时，预测时域中控制输入v_1∼_η（k + i|k）的上、下界.

1）当k >1时，根据式（10）的第2 子式可知，输入 v_1∼_η（k + i|k），i = 0，1，· · ·，N − 1的上、下界皆是时变约束，分别对应下述系列线性优化问题的解:

\begin{matrix} {\underline{v}}_{1 \sim η} (k + i ∣ k) = \underset{u (k + i ∣ k)}{m i n} h (\cdot, \cdot, k + i ∣ k), \\ s . t . u (k + i ∣ k) \in U, \end{matrix}

(12)

\begin{matrix} {\bar{v}}_{1 \sim η} (k + i ∣ k) = \underset{u (k + i ∣ k)}{m a x} h (\cdot, \cdot, k + i ∣ k), \\ s . t . u (k + i ∣ k) \in U . \end{matrix}

(13)

进而，新输入约束可表示为

v_{p} (k + i ∣ k) \in V_{p, k + i ∣ k}, p = 1,2, \dots, η,

(14)

其中

V_{p, k + i ∣ k} = \{v_{p} \in R^{r_{p}} ∣ {\underline{v}}_{p} (k + i ∣ k) < v_{p} < {\bar{v}}_{p} (k + i ∣ k)\} .

2）当k = 0时，根据式（10）的第1子式可知，当前时刻的跟踪误差

e_{p}^{⌊0 \sim μ_{p} - 1⌋} （ k ）

已知，误差预测输入序列

V_{e_{p}}

（k + j − 1|k）和其约束的上、下界未知. 这里将输入v_1∼_η（k +i|k），i = 0，1，· · ·， N −1的上、下界设为由状态初值

x_{p}^{⌊0 \sim μ_{p} - 1⌋}

（0）和输入约束u（0）∈ U 所确定的常值约束边界. 输入v_1∼_η（k + i|k），i= 0，1，· · ·，N − 1 约束的下界为

{\underline{v}}_{1 \sim η} (k + i ∣ k) = {\underline{v}}_{1 \sim η} (0),

(15)

其中

\begin{matrix} {\underline{v}}_{1 \sim η} (0) = \underset{u (0)}{m i n} h (X (0), u (0)), \\ s . t . u (0) \in U . \end{matrix}

输入v_1∼_η（k + i|k）约束的上界为

{\bar{v}}_{1 \sim η} (k + i ∣ k) = {\bar{v}}_{1 \sim η} (0),

(16)

其中

\begin{matrix} {\bar{v}}_{1 \sim η} (0) = \underset{u (0)}{m a x} h (X (0), u (0)), \\ s . t . u (0) \in U . \end{matrix}

注 2 当r = 1时，系统（1）表示单变量系统，此时优化问题（12）–（13）和（15）–（16）均为带有线性标量优化函数的线性优化问题，且其约束空间是线性可行的约束集，则最优解一定存在且唯一，因此可以直接求解优化问题（12）–（13）和（15）–（16）. 当r >1时，优化问题（12）–（13）和（15）–（16）则为多目标优化问题. 常见的多目标优化问题处理方法包括将向量值目标函数转化为标量目标函数的方法，如帕累托最优方法、裁剪帕累托边界的各部分约束方法和目标之间的权重法等 ^[21] . 鉴于本文涉及的控制输入约束为线性凸空间，本文采用等加权和法将多变量优化问题转为为标量函数优化问题，因此同样可以直接求得其优化解.

步骤 3 预测指标解耦与优化求解.

当系统中输入和状态约束同时存在时，由于系统的物理限制，需要严格满足输入饱和约束，而通过松弛状态约束以保证预测控制中优化问题的可解性. 故在滚动优化指标（5）引入状态松弛因子，具体如下:

J^{'} (k) = \sum_{p = 1}^{η} J_{p}^{'} (k),

(17)

其中

\begin{matrix} J_{p}^{'} (k) = \\ \frac{1}{2} \sum_{i = 0}^{N - 1} ({‖e_{p}^{⌊0 \sim μ_{p} - 1⌋} (k + i ∣ k)‖}_{Q_{p}}^{2} + \\ {‖V_{e_{p}} (k + i ∣ k)‖}_{R_{p}}^{2}) + \\ \frac{1}{2} {‖e_{p}^{⌊0 \sim μ_{p} - 1⌋} (k + N ∣ k)‖}_{F_{p}}^{2} + {‖ε_{p} (k)‖}_{S_{p}}^{2}, \end{matrix}

(18)

其中: S_p>0是惩罚项的权重矩阵;

ε_{p} （ k ） \in R^{r_{p}}

是状态约束松弛项; 状态约束松弛为

x_{p} （ k ） \in X_{p}^{'} \subseteq R^{r_{p}} ， X_{p}^{'} = \{z_{p} \in R^{μ_{p} r_{p}} ∣ G_{p} z_{p} ⩽ g_{p} + ε_{p}\} .

最小化系统预测滚动优化指标（17）的优化问题，具体为

\underset{\begin{matrix} V_{e_{p}} (k + i ∣ k), ε_{p} (k), i = 0, 1, \dots, N - 1 \end{matrix}}{m i n} J_{p}^{'} (k), p = 1, 2, \dots, η,

s.t. x_{p}^{⌊0 \sim μ_{p} - 1⌋} (k + i + 1 ∣ k) \in X_{p}^{'},

v_{p} (k + 1 ∣ k) \in V_{p, k + j ∣ k}

(19)

基于步骤1–3，全驱预测级联控制算法可整理为算法1（见表1）.

3.1 稳定性分析

在稳定性分析之前，结合文献 ^[13] 和文献 ^[22] 介绍本节用到的重要引理.

考虑下述线性系统:

x (k + 1) = A x (k) + B u (k),

(20)

其中: x和u分别表示状态和输入，（A，B）是可控矩阵对. 定义下述滚动时域指标:

J (k) = \frac{1}{2} \sum_{i = 0}^{N - 1} (‖ x (k + i ∣ k) ‖_{Q}^{2} + ‖ u (k + i ∣ k) ‖_{R}^{2}) + ‖ x (k + N ∣ k) ‖_{F}^{2},

其中: F ≥ 0，G ≥ 0和R >0是预测权重.

在可行的混合约束下的优化问题表示为

\underset{\begin{matrix} u (k + i ∣ k) \\ i = 0, 1, \dots, N - 1 \end{matrix}}{m i n} J_{p} (k),

s.t. {\underline{u}}_{k} ⩽ u (k + i ∣ k) ⩽ {\bar{u}}_{k}, i = 0, 1, \dots, N - 1,

G x (k + j ∣ k) ⩽ g, j = 1,2, \dots, N,

(21)

其中

{\underline{u}}_{k} ， {\bar{u}}_{k} ，

G和g是已知矩阵（向量/常数）.

引理 1 如果预测参数和系统初值满足:

1) A^TF (I + BR⁻¹B^TF) ⁻¹A + Q – F ≤ 0;

2) Gx (0) ≤ g;

3) N ≥ n,

则存在优化问题（21）的解作为控制器u（k）= u（k|k），使系统（20）是渐近稳定且满足可行约束.

表1算法1: 全驱级联预测控制算法

Table1Algorithm 1: Fully cascade predictive control algorithm

在上述引理的基础上，本文给出下述结论.

x_{p}^{⌊0 \sim μ_{p} - 1⌋} (0) \in X_{p}, p = 1, 2, \dots, η;

N ⩾ m a x (r_{p}, p = 1, 2, \dots, η);

A_{p}^{T} F_{p} {(I_{r p} + B_{p} R_{p}^{- 1} B_{p}^{T} F_{p})}^{- 1} A_{p} + Q_{p} - F_{p} ⩽ 0,

p = 1, 2, · · ·, η;

4) Q_p>0, F_p >0, R_p >0, p = 1, 2, · · ·, η,

其中A_p和B_p由式（7）给出，那么由表1的算法1所求系统的控制器（4）使得

1）滚动优化指标（17）最小;

2）状态渐近跟踪参考信号，即当 k → ∞时，x_p（k）→ r_p（k），p = 1，2，· · ·，η;

3）对应的闭环系统是渐近稳定的.

证结论（1）是求解优化问题（19）的直接结果.

对于结论（2）–（3），k 时刻优化问题（19）的解记为

v_{e_{p}}^{*} （ k + i ∣ k ） ， i = 0，1 ， \dots ， N - 1 和 ε_{p}^{*} （ k ） .

在k + 1时刻，上述控制序列是优化问题（19）在k + 1时刻的可行解，

\begin{matrix} V_{e_{p}} (k + i ∣ k + 1) = \\ V_{e_{p}}^{*} (k + i ∣ k), i = 1, 2, \dots, N - 1, \\ ε_{p} (k + 1) = ε_{p}^{*} (k) . \end{matrix}

根据条件1），优化问题（19）在k = 0 时刻存在可行解. 通过数学归纳法可知，优化问题（19）在k >0时总存在可行解. 结合引理1以及条件（2）–（4），下述不等式成立:

\begin{matrix} J_{p}^{*} (e_{p}^{⌊μ_{p} - 1⌋} (k), k) ⩾ \\ {‖e_{p}^{⌊0 \sim μ_{p} - 1⌋} (k)‖}_{Q_{p}}^{2} + {‖V_{e_{p}} (k)‖}_{R_{p}}^{2} + \\ J_{p}^{*} (A_{p} e_{p}^{⌊0 \sim μ_{p} - 1⌋} (k) + B_{p} V_{e_{p}} (k), k + 1) . \end{matrix}

即根据算法1所确定的

V_{e_{p}}

（k）可以使得对应的闭环系统（6）是渐近稳定的. 故结论2）和结论3）成立. 证毕.

4 案例

4.1 航天器姿态控制系统

考虑航天器姿态系统 ^[23-24]，其前向差分离散下的系统形式如下:

q^{⌊ 1 ⌋} (k + 1) = f (q^{⌊ 0 \sim 1 ⌋} (k)) + B (q^{⌊ 0 \sim 1 ⌋} (k)) u (k),

(22)

其中: q = [φ ϑ ψ]^T表示航天器的姿态欧拉角，u∈

R

³ 为控制输入，输入配置矩阵B（·）∈

R

^3×3和非线性向量f（·）∈

R

³具体如下:

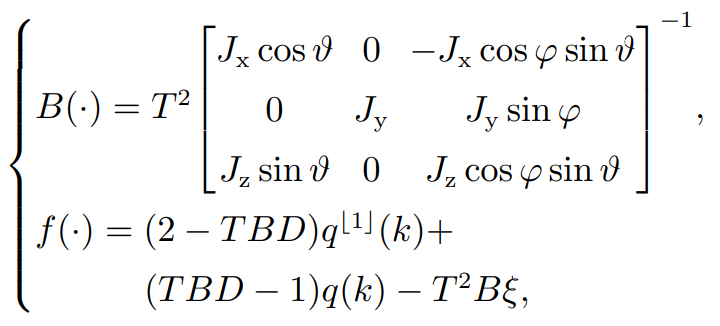
式中: J_x，J_y，J_z是惯性矩; D（·）和ξ（·）的具体形式参考文献 ^[23] .

当φ ∈

(\frac{- π}{2} ， \frac{π}{2})

时，

d e t B = \frac{1}{I_{x} I_{y} I_{z} c o s φ} \neq 0

则系统（22）是亚全驱系统，可行集为

q (k) \in Q ≜ \{q_{1 \sim 3} \in R^{3} |q_{2} \in (- \frac{π}{2}, \frac{π}{2})\}, \forall k ⩾ 0 .

令J_x = 18，J_y = 21，J_z = 24，控制输入约束为

u (k) \in U ≜ \{u_{1 \sim 3} \in R^{3} | | u_{i} ∣ ⩽ 10, i = 1, 2, 3\} .

如图2–3所示，为无输入约束和带输入约束的航天器姿态系统响应曲线. 考虑有无输入约束的两种情况，图2为系统三通道输入响应曲线，图3为系统的姿态状态响应曲线. 可以看出，所提出的控制算法在确保系统状态收敛的同时满足了上述输入和状态约束条件.

图2航天器系统姿态响应曲线

Fig.2Attitude response curves of the spacecraft system

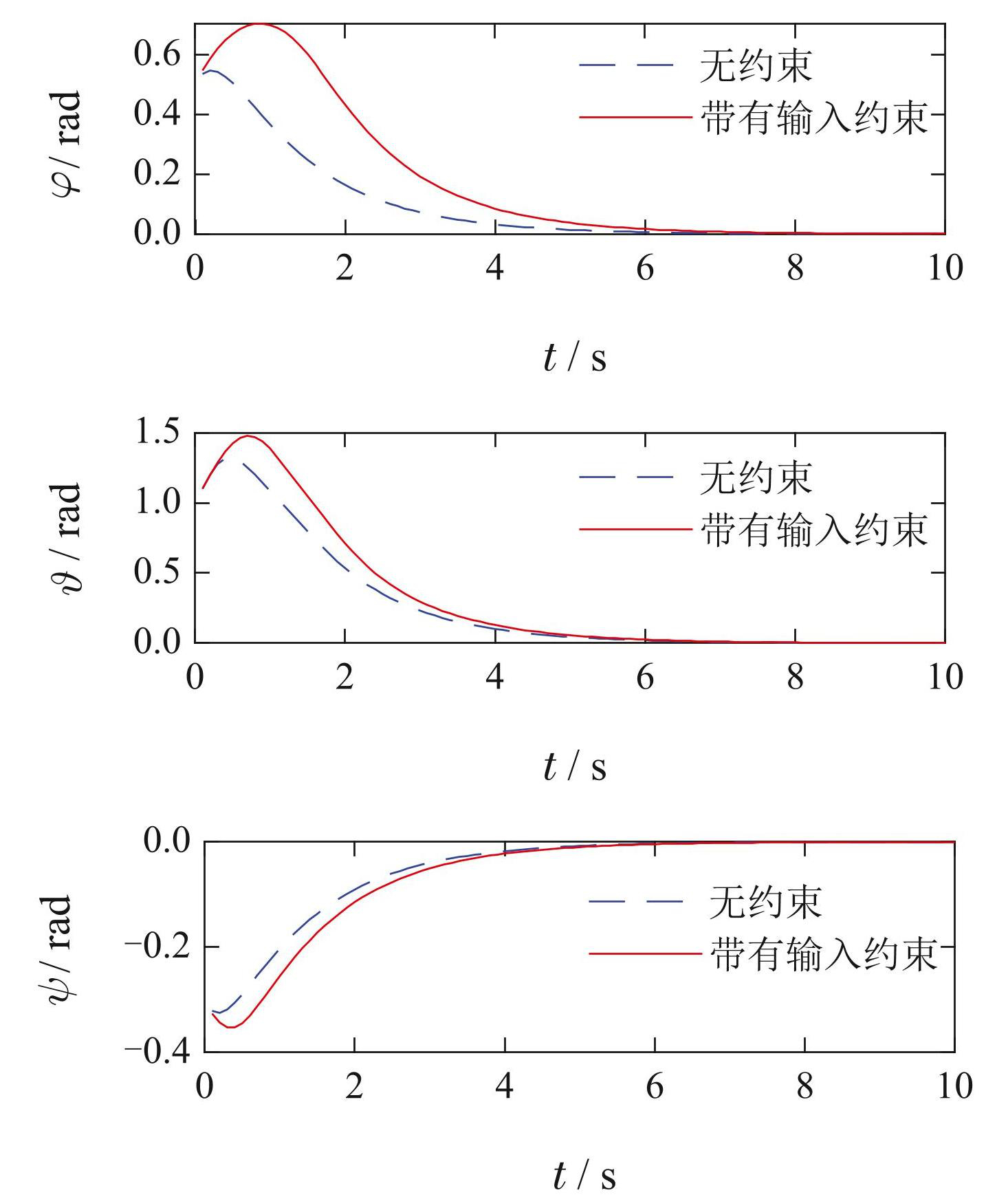
图3航天器系统输入响应曲线

Fig.3Input response curves of the spacecraft system

4.2 航天器消旋系统

如图4所示的欠驱旋转平移驱动系统是一种典型的欠驱系统，同为双自旋航天器的简化模型，其动力学方程如下 ^[25-26] :

\{\begin{matrix} (M + m) \ddot{x} + m l c o s θ \ddot{θ} = m l {\dot{θ}}^{2} s i n θ + s x \\ m l c o s θ \ddot{x} + (J + m l^{2}) \ddot{θ} + m g l s i n θ = τ \end{matrix}

(23)

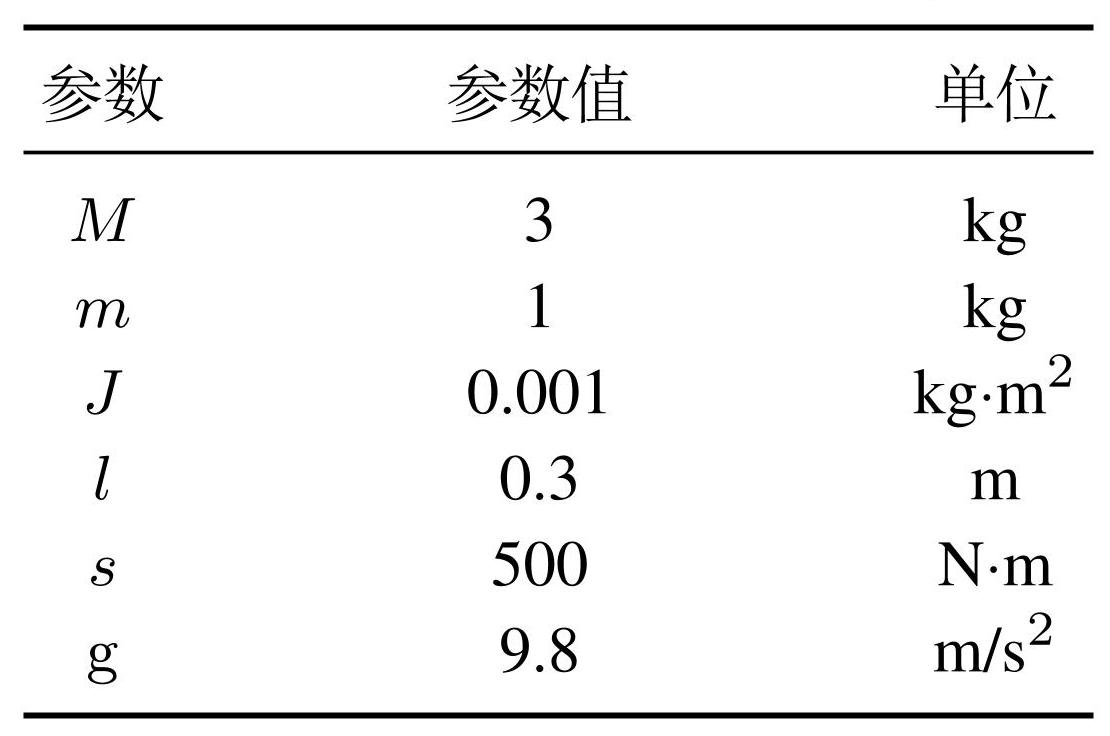
其中: x表示车的水平位移，θ ∈（−π/2，π/2）表示转子相对于垂直方向的旋转角度，g为重力加速度，M和m表示小车和偏心球的质量，J为转子的转动惯量，s表示弹簧的弹性系数，l表示偏心球的旋转半径. 系统的参数选取见表2.

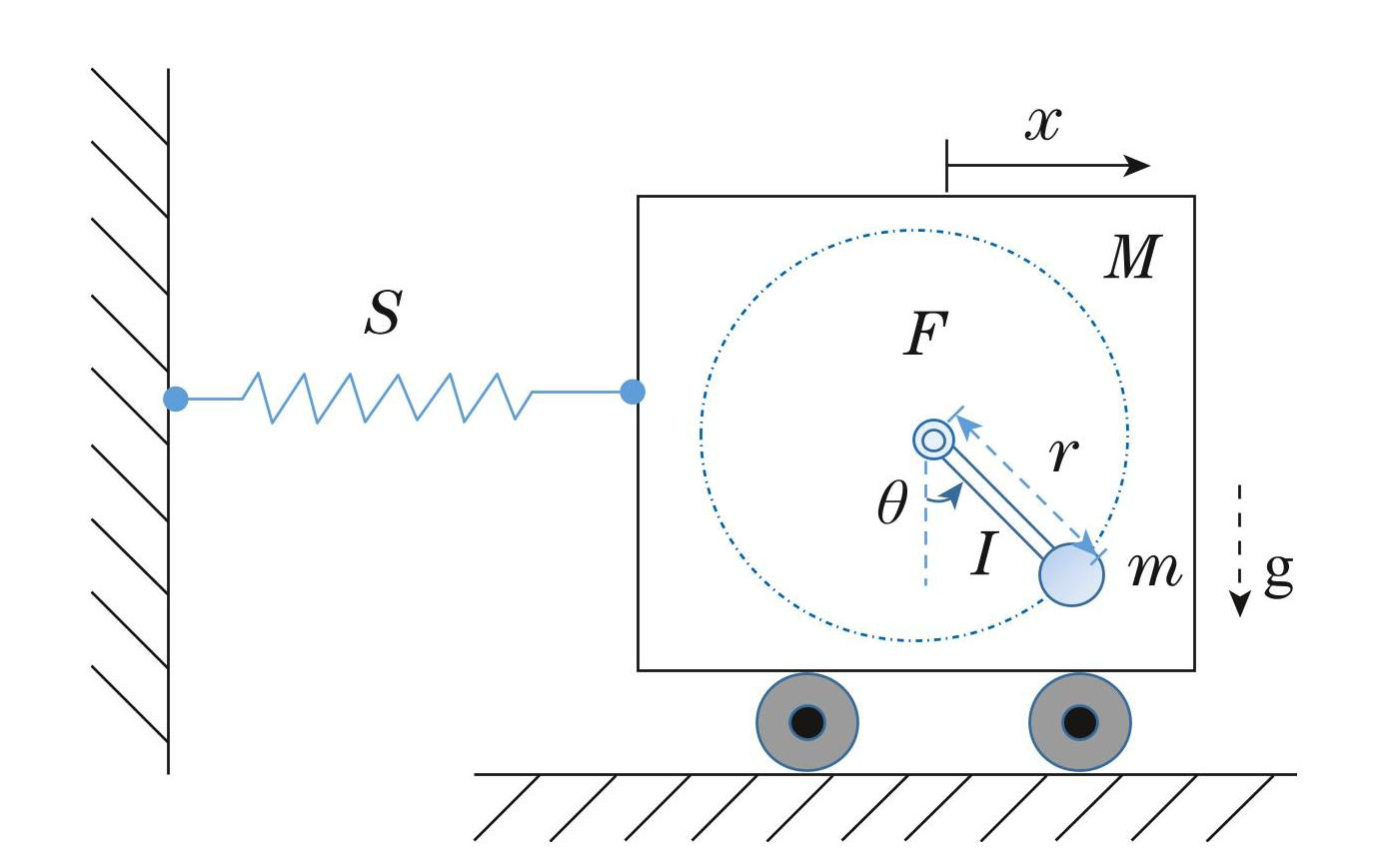
图4RTAC系统结构

Fig.4The structure of the RTAC system

表2RTAC系统的参数表

Table2Parameters of RTAC system

采用下述同胚变换:

z^{(0 \sim 3)} = [\begin{matrix} x + \frac{m l}{M + m} s i n θ \\ \dot{x} + \frac{m l}{M + m} c o s θ \dot{θ} \\ - \frac{s x}{M + m} \\ - \frac{s \dot{x}}{M + m} \end{matrix}]

(24)

系统（23）前向差分离散可得下述非线性全驱系统:

\begin{matrix} z^{⌊ 3 ⌋} (k + 1) = \\ F (z^{⌊ 0 \sim 3 ⌋} (k), T) + \\ B (z^{⌊ 0 \sim 3 ⌋} (k), T) τ (k), z^{⌊ 0 \sim 3 ⌋} (k) \in Z, \end{matrix}

(25)

其中:

\{\begin{matrix} F (\cdot) = B (\frac{f^{' 2}}{2 {(1 - f^{2})}^{3 / 2}} - \frac{(M + m) Δ^{2} z (k)}{m l \sqrt{1 - f^{2}}}) + \\ 4 z^{⌊ 3 ⌋} (k) - 6 z^{⌊ 2 ⌋} (k) + 4 z^{⌊ 1 ⌋} (k) - z (k), \\ B (\cdot) = \frac{s m l T^{4} \sqrt{1 - f^{2}}}{(M + m)^{2}}, \\ f (\cdot) = \frac{M + m}{m l} z (k) + \frac{(M + m)^{2} (Δ^{2} z (k))}{s m l}, \\ f^{'} (\cdot) = \frac{(M + m) Δ^{1} z (k)}{m l} + \frac{(M + m)^{2} Δ^{3} z (k)}{s m l}, \end{matrix}

其中T为采样时间，离散所需的差分算子运算满足

Δ^{i} x (k) = \frac{\sum_{j = 0}^{i - 1} (- 1)^{j + 1} C_{i}^{j} x (k + j)}{T^{i}},

旋转角约束离散化结果记为

z^{⌊ 0 \sim 3 ⌋} (k) \in Z ≜ \{z_{1 \sim 4} \in R^{4} ∣ H z_{1 \sim 4} < h\}

其中:

H = [\begin{matrix} \frac{M + m + s T^{2}}{s T^{2}} & - 2 \frac{M + m}{s T^{2}} & \frac{M + m}{s T^{2}} & 0 \\ - \frac{M + m + s T^{2}}{s T^{2}} & 2 \frac{M + m}{s T^{2}} & - \frac{M + m}{s T^{2}} & 0 \end{matrix}],

h = [\begin{matrix} \frac{m l}{M + m} \\ - \frac{m l}{M + m} \end{matrix}]

根据同胚变换式（24），变换前的状态为

\{\begin{matrix} x (k) = - \frac{(M + m) (Δ^{2} z (k))}{s}, \\ θ (k) = \\ a r c s i n (\frac{M + m}{m l} (\frac{M + m}{s T^{2}} (Δ^{2} z (k)) + z (k))) . \end{matrix}

为了验证方法的有效性，本文将提出的全驱预测算法（fully actuated system predictive control，FAS-PC）与状态空间下模型线性化后的线性模型预测控制（linear model predictive control，LMPC）算法及直接非线性优化的非线性预测控制（nonlinear predictive control，NMPC）算法进行仿真对比. 通过对RTAC系统（23）进行前向差分，得到其在状态空间下的离散形式为

z (k + 1) = f (z (k)) + B (z (k)) u (k)

(26)

其中:

f (\cdot) = [\begin{matrix} z_{2} (k) \\ \frac{(J + m l^{2}) f_{1} (k) + m l c o s z_{3} (k) f_{2} (k)}{(M + m) (J + m l^{2}) - m^{2} l^{2} {c o s}^{2} z_{3} (k)} \\ z_{4} (k) \\ \frac{- (J + m l^{2}) f_{2} (k) - m l c o s z_{3} (k) f_{1} (k)}{(M + m) (J + m l^{2}) - m^{2} l^{2} {c o s}^{2} z_{3} (k)} \end{matrix}],

f_{1} (\cdot) = m l z_{4}^{2} (k) s i n z_{3} (k) + s z_{1} (k),

f_{2} (\cdot) = m g l s i n z_{3} (k),

B (\cdot) = [\begin{matrix} 0 \\ - m l c o s z_{3} (k) \\ 0 \\ M + m \end{matrix}],

z (k) = z_{1 \sim 4} (k) = {[x (k) x^{⌊ 1 ⌋} (k) θ (k) θ^{⌊ 1 ⌋} (k)]}^{T} .

将上述RTAC系统在原点进行线性化后，得到线性化的状态空间系统模型为

z (k + 1) = A z (k) + B u (k),

(27)

其中:

状态空间模型下的滚动优化指标记为

J (k) = \frac{1}{2} \sum_{i = 0}^{N - 1} (‖ z (k + i ∣ k) ‖_{Q}^{2} +

‖ u (k + i ∣ k) ‖_{R}^{2}) + \frac{1}{2} ‖ z (k + N ∣ k) ‖_{F}^{2} .

(28)

RTAC系统（25）的输入约束设为

u (k) \in U ≜ {u \in R ∣ - 10 ⩽ u ⩽ 10}, k ⩾ 0 .

3 种预测方法实现的对比元素见表3，采用相同的状态初值条件、采样时间、预测时域和预测权重，分别设置为:

z^{⌊ 0 \sim 3 ⌋} （ 0 ） = {[\begin{matrix} 0.001 0.001 0.001 - 0.002 \end{matrix}]}^{T} ，

T = 0.1 s，N = 15，Q = 0.9I4，R = 0.1，F = diag{1.040 2，2.174，3.288 1，4.352 1}，S = 2I₄.

表3预测控制方法

Table3Predictive control methods

同时，本文采用均方误差（mean squared error，MSE）衡量状态跟踪误差，以评估系统输出和期望值之间的偏差; 平均CPU时间用来评估算法的复杂度以及实时性; 控制输入的均方值（mean squared control input，MSCI）用于分析控制输入的能量.

3 种算法对应的系统指标和系统响应曲线分别如表4所示和图5所示. 与LMPC和NMPC相比较，所提的全驱预测级联优化算法在输入约束条件下，能够以较快的响应速度，使RTAC系统实现快速镇定，状态的均方误差较小，所需要的控制能量较低，并确保系统输入不超过约束范围.

表4RTAC系统的性能指标

Table4Performance indicators of the RTAC system

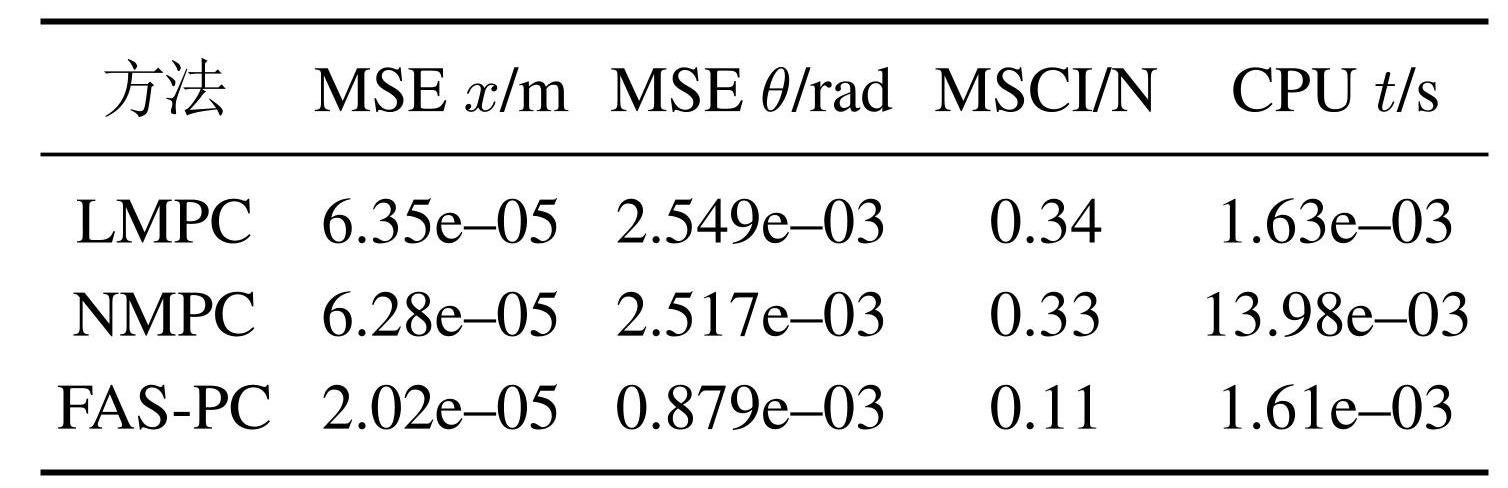
图5RTAC系统响应曲线

Fig.5Response curves of the RTAC system

5 结论

本文针对具有输入饱和的非线性混合阶全驱系统，提出了一种基于级联优化的预测控制方法，实现了对参考信号的跟踪控制的控制目标. 所设计的双层优化预测级联控制器巧妙地规避了非线性输入变换所引入的复杂非线性约束，同时通过引入状态松弛因子，有效保证了优化问题的可解性. 在此基础上，本文探讨了预测参数与闭环系统稳定性之间的内在关系，为控制器设计提供了坚实的理论支撑.

未来的研究将进一步聚焦于外界不确定性、模型误差以及环境干扰对系统性能的影响，致力于开发更具鲁棒性的预测控制策略. 此外，结合自适应机制，研究将力求提升控制器在动态未知环境中的自适应能力，以满足复杂环境下全驱系统的严苛控制需求. 同时，还将关注控制算法的实时性优化与工程化实现，推动高效、可靠的预测控制方法在实际应用中的落地，为工业场景中的复杂控制问题提供创新性解决方案.

图1全驱系统级联预测控制系统框图

Fig.1The block diagram of cascaded predictive control for FASs

下载: 全尺寸图片

图2航天器系统姿态响应曲线

Fig.2Attitude response curves of the spacecraft system

下载: 全尺寸图片

图3航天器系统输入响应曲线

Fig.3Input response curves of the spacecraft system

下载: 全尺寸图片

图4RTAC系统结构

Fig.4The structure of the RTAC system

下载: 全尺寸图片

图5RTAC系统响应曲线

Fig.5Response curves of the RTAC system

下载: 全尺寸图片

表1算法1: 全驱级联预测控制算法

Table1Algorithm 1: Fully cascade predictive control algorithm

下载: 全尺寸图片

表2RTAC系统的参数表

Table2Parameters of RTAC system

下载: 全尺寸图片

表3预测控制方法

Table3Predictive control methods

下载: 全尺寸图片

表4RTAC系统的性能指标

Table4Performance indicators of the RTAC system

下载: 全尺寸图片

图1全驱系统级联预测控制系统框图

Fig.1The block diagram of cascaded predictive control for FASs

图2航天器系统姿态响应曲线

Fig.2Attitude response curves of the spacecraft system

图3航天器系统输入响应曲线

Fig.3Input response curves of the spacecraft system

图4RTAC系统结构

Fig.4The structure of the RTAC system

图5RTAC系统响应曲线

Fig.5Response curves of the RTAC system

表1算法1: 全驱级联预测控制算法

Table1Algorithm 1: Fully cascade predictive control algorithm

表2RTAC系统的参数表

Table2Parameters of RTAC system

表3预测控制方法

Table3Predictive control methods

表4RTAC系统的性能指标

Table4Performance indicators of the RTAC system

图1全驱系统级联预测控制系统框图

Fig.1The block diagram of cascaded predictive control for FASs

图2航天器系统姿态响应曲线

Fig.2Attitude response curves of the spacecraft system

图3航天器系统输入响应曲线

Fig.3Input response curves of the spacecraft system

图4RTAC系统结构

Fig.4The structure of the RTAC system

图5RTAC系统响应曲线

Fig.5Response curves of the RTAC system

表1算法1: 全驱级联预测控制算法

Table1Algorithm 1: Fully cascade predictive control algorithm

表2RTAC系统的参数表

Table2Parameters of RTAC system

表3预测控制方法

Table3Predictive control methods

表4RTAC系统的性能指标

Table4Performance indicators of the RTAC system

LI Shaoyuan. Model-based predictive control for industrial processa survey. Control Engineering of China,2010,17(4):407-415.(李少远. 工业过程系统的预测控制. 控制工程,2010,17(4):407-415.)

CHEN Hong. Model Predictive Control. Beijing: Science Press,2013.(陈虹. 模型预测控制. 北京: 科学出版社,2013.)

DING Baocang. Theory and Method of Predictive Control(2nd edition). Beijing: Science Press,2017.(丁宝苍. 预测控制的理论与方法(第2版). 北京: 科学出版社,2017.)

HE Defeng, CAO Peiyi, CEN Jianghui. Utopia multi-objective safe predictive control of constrained nonlinear systems. Control Theory & Applications,2024,41(2):355-363.(何德峰, 操佩颐, 岑江晖. 约束非线性系统理想点多目标安全预测控制. 控制理论与应用,2024,41(2):355-363.)

SCHWENZER M, AY M, BERGS T,et al. Review on model predictive control: An engineering perspective. The International Journal of Advanced Manufacturing Technology,2021,117(5):1327-1349.

HEWING L, WABERSICH K P, MENNER M,et al. Learning-based model predictive control: Toward safe learning in control. Annual Review of Control, Robotics,and Autonomous Systems,2020,3(1):269-296.

MORATO M M, NORMWY-RICO J E, SENAME O. Model predictive control design for linear parameter varying systems: A survey. Annual Reviews in Control,2020,49:64-80.

ZHAI M, SUN N, YANG T,et al. Underactuated mechanical systems with both actuator and actuated/unactuated state constraints: A predictive control-based approach. IEEE/ASME Transactions on Mechatronics,2022,28(3):1359-1371.

YANG T, SUN N, ZHAI M,et al. Data-based dual-loop learning control of underactuated systems with disturbance prediction and input-output constraints. IEEE Transactions on Artificial Intelligence,2022,5(7):3419-3430.

SCHWENZER M, AY M, BERGS T,et al. Review on model predictive control: An engineering perspective. The International Journal of Advanced Manufacturing Technology,2021,117(5):1327-1349.

GRIMBLE M J, MAJECKI P, GRIMBLE M J,et al. Linear and nonlinear predictive optimal control. Nonlinear Industrial Control Systems: Optimal Polynomial Systems and State-Space Approach,2020:291-344.

WANG X B, DUAN G R. High-order fully actuated system approaches: Model predictive control with applications to under-actuated systems. Journal of the Franklin Institute,2023,360(10):6953-6975.

WANG X B, DUAN G R. Fully actuated system approaches:predictive elimination control for discrete-time nonlinear time-varying systems with full state constraints and time-varying delays. IEEE Transactions on Circuits and Systems I: Regular Papers,2024,71(1):383-396.

DUAN G R. High-order fully actuated system approaches: Part I. Models and basic procedure. International Journal of Systems Science,2021,52(2):422-435.

DUAN G R. High-order fully actuated system approaches: Part X. Basics of discretetime systems. International Journal of Systems Science,2022,53(4):810-832.

DUAN G R. Robust stabilization of time-varying nonlinear systems with time-varying delays: A fully actuated system approach. IEEE Transactions on Cybernetics,2023,53(12):7455-7468.

DUAN G R. Stabilization of four types of underactuated systems: A FAS approach. International Journal of Systems Science,2024,55(12):2421-2441.

ZHANG Z, DUAN G. Stabilization controller of an extended chained nonholonomic system with disturbance: An FAS approach. IEEE/CAA Journal of Automatica Sinica,2024,11(5):1262-1273.

HE D, WANG L, SUN J. On stability of multiobjective NMPC with objective prioritization. Automatica,2015,57:189-198.

LEE J, KWON W H, CHOI J. On stability of constrained receding horizon control with finite termial weighting matrix. Automatic,1998,34(12):1607-1612.

ZHANG D W, LIU G P, CAO L. Coordinated control of high-order fully actuated multiagent systems and its application: A predictive control strategy. IEEE/ASME Transactions on Mechatronics,2022,27(6):4362-4372.

ZHANG D W, LIU G P, CAO L. Constrained cooperative control for high-order fully actuated multiagent systems with application to airbearing spacecraft simulators. IEEE/ASME Transactions on Mechatronics,2023,28(3):1570-1581.

DUAN G R. High-order fully actuated system approaches: Part VIII. Optimal control with application in spacecraft attitude stabilisation. International Journal of Systems Science,2022,53(1):54-73.

DUAN Guangren. Quasi-linear system approaches for flight vehicle control-part 1:an overview and problems. Journal of Astronautics,2020,41(6):633-646.(段广仁. 飞行器控制的伪线性系统方法-第1部分: 综述与问题. 宇航学报,2020,41(6):633-646.)

TAN P, SUN M, SUN Q,et al. Linear stabilization control for underactuated RTAC based on model reconstruction. IEEE/ASME Transactions on Mechatronics,2021,27(3):1640-1650.

AVIS J M, NERSESOV S G, NATHAN R,et al. A comparison study of nonlinear control techniques for the RTAC system. Nonlinear Analysis: Real World Applications,2010,11(4):2647-2658.