欢迎访问《控制理论与应用》期刊网站！

考虑温度影响的FCHEV等效燃油消耗最优控制策略

doi: 10.7641/CTA.2025.40306

付江涛，司秀丽，来国梁，刘佳豪

河南科技大学信息工程学院, 河南洛阳 471009

基金项目: 国家自然科学基金项目(61473115)资助.

详细信息

作者简介

付江涛副教授,博士,目前研究方向为为电动汽车驱动与系统控制,E-mail: fujiangtao@haust.edu.cn;

司秀丽硕士研究生,目前研究方向为混合动力汽车系统建模、控制与优化,E-mail: 3041471187@qq.com;

来国梁硕士研究生,目前研究方向为混合动力汽车系统建模与模式切换控制算法设计,E-mail: 1715765979@qq.com;

刘佳豪硕士研究生,目前研究方向为混合动力汽车动力系统控制结构建模和仿真设计,E-mail: ljh2522335299@163.com.

通信作者

付江涛，E-mail: fjtmengnan302@sina.com.cn;Tel.:+8613939921746

Best equivalent hydrogen consumption control strategy for fuel cell vehicle considering temperature affection

FU Jiang-tao ， SI Xiu-li ， LAI Guo-liang ， LIU Jia-hao

College of Electronic Information Engineering, Henan University of Science and Technology, Luoyang Henan 471009 , China

Funds: Supported by the National Natural Science Foundation of China (61473115).

摘要

燃料电池堆(FCS)是新能源汽车应用的一种主要能源, 等效燃油经济性是许多研究人员关注的问题. 本文提出了一种自适应的实施控制策略, 通过在燃料电池和动力电池之间进行功率需求的分配, 实现最优的等效燃油经济性. 为了在控制策略中体现温度的影响, 建立了包含热模型的FCS模型以及包含了温度的动力电池模型. 通过贝叶斯估计理论预测未来的功率需求. 基于FCS模型、电池模型和预测的功率需求, 设计了实时控制策略, 并在优化范围内以庞特里亚金最小化原理进行优化. 通过仿真和硬件在环(Hil)实验在40 kW的FCS上验证了所提出的控制策略. 通过和基于规则的策略(RB)以及和最小损失策略(LMS)的对比表明, 在考虑温度影响的情况下, 本文所提出的控制策略可以有效地将等效燃料消耗降低4%.

关键词

混合动力电动汽车(HEV) / 燃料电池系统 / 优化控制 / 荷电状态(SOC) / 功率需求预测 / 等效燃油经济性

Abstract

Fuel cell stack (FCS) is one of the primary energy sources for the application of new energy vehicles, and the equivalent fuel economy is a focal point of concern for many researchers. This article proposes an adaptive implementation control strategy to achieve optimal equivalent fuel economy by allocating power demand between the fuel cell and the power battery. In order to incorporate the influence of temperature into the control strategy, an FCS model with a thermal model and a power battery model considering temperature are established. Bayesian inference is employed to analyze and predict future power demand. Based on the FCS model, battery model, and predicted power demand, a real-time control strategy is designed, and optimization is conducted within the Pontryagin minimum principle. The proposed control strategy is validated through simulations and hardware-in-the-loop (Hil) experiments on an FCS with power of 40 kW. Comparison with rule-based control strategy and loss minimum strategy indicates that, considering the influence of temperature, the proposed control strategy effectively reduces equivalent fuel consumption by 4%.

Keywords

hybrid electric vehicle (HEV) / fuel cell system / optimal control / state of charge (SOC) / power requirement prediction / equivalent fuel economy

1 引言 2 问题描述 2.1 包含温度的电池模型 2.2 功率需求预测 3 优化控制策略 3.1 目标函数 3.2 实时控制 4 仿真和实验验证 5 结论

1 引言

燃料电池混合动力汽车是一种很有前途的交通措施，因为其使用清洁能源，所以零排放无污染 ^[1-2] . 燃料电池堆（fuel cell stack，FCS）和电池通常集成在动力传动系统中，以驱动车辆. 如何在两种能源之间分配功率需求以获得良好的等效燃油经济性已成为一个重要的研究问题 ^[3-4] .

为了实现良好等效燃油经济性的动力分配，设计了许多不同的控制策略来分配动力需求. 基于规则的控制策略因其可靠性和执行简单而被广泛使用，但设计规则需要大量的经验数据和相关专业知识，一旦该策略被设计用于某一车辆配置，就很难用于其他车辆配置，即该策略泛化能力有限 ^[5-7] . 为了获得更好的优化结果，通过使用不同的算法，如动态规划 ^[8-9]、庞特里亚金最小值原理 ^[10-11]，设计了基于优化的控制策略. 文献 ^[12-14] 中提出了一些基于庞特里亚金最小值原理推导出的等效燃油消耗最优控制策略，这些控制策略具有良好的实施执行的能力，但等效因子应首先根据预先的实验确定或校准. 文献 ^[15] 和文献 ^[16] 中，模型预测控制（model predictive control，MPC）策略也被广泛用于处理驾驶工况信息，如速度预测和功率需求预测. 近来基于神经元网络的控制策略也被应用于离线车辆的控制，基于大量训练数据样本的数据驱动神经元网络控制策略被用于离线车辆 ^[17-18] .

在上述控制策略中，它们通常可分为两类: 1）预知驾驶工况信息，控制策略通过最小值原理和动态规划的方法来决定控制策略中的控制变量实现等效燃油经济性. 它们通常可以作为比较的标准，而不是实时应用; 2）驾驶工况信息事先未知，可以使用损失最小化策略和自适应控制律等方法来设计策略. 通常，这些类型的控制策略可以用于实时应用，但可能需要二次优化. 本文针对等效燃油经济性设计了一种实时控制策略，并试图从最优解中获得一个自适应因子，而控制策略中的自适应因子主要用于对未来的功率需求的预测.

在设计控制策略时，应控制电池以提高系统的燃油经济性，并延长电池寿命 ^[19-22] . 代价函数中包括了电池老化模式，并研究了电池输出电流对总能耗的影响. 文献 ^[23-26] 还研究了等效燃料经济性和电池健康度之间的平衡性能，通过对目标函数施加软约束，在电池温度和燃料消耗之间进行权衡，以优化混合动力传动系的功率管理. 电池温度严重影响电池的老化过程. 为了减少电池温度对等效燃油经济性的影响，延长电池寿命，所提出的控制策略在实现功率需求分配时考虑了电池温度.

本文的其余部分组织如下: 第2节介绍了优化问题，包括电池模型和功率需求预测; 第3节详细介绍了基于最小化原理和拉格朗日系数估计的实时控制策略; 在第4节中，通过仿真和试验台实验对控制策略进行了验证，并将结果与过去的一些方法进行了比较; 最后，第5节总结了拟议工作的结论和未来的改进.

2 问题描述

为了简化控制策略的设计，考虑到能量流和电气拓扑，燃料电池汽车（fuel cell hybrid electric vehicles，FCHEV）的架构如图1所示. 质子交换膜燃料电池系统（proton exchange membrane fuel cells，PEMFCS）总是向电气总线提供电力，电池可以向电气总线供电，也可以从电气总线接收电力.

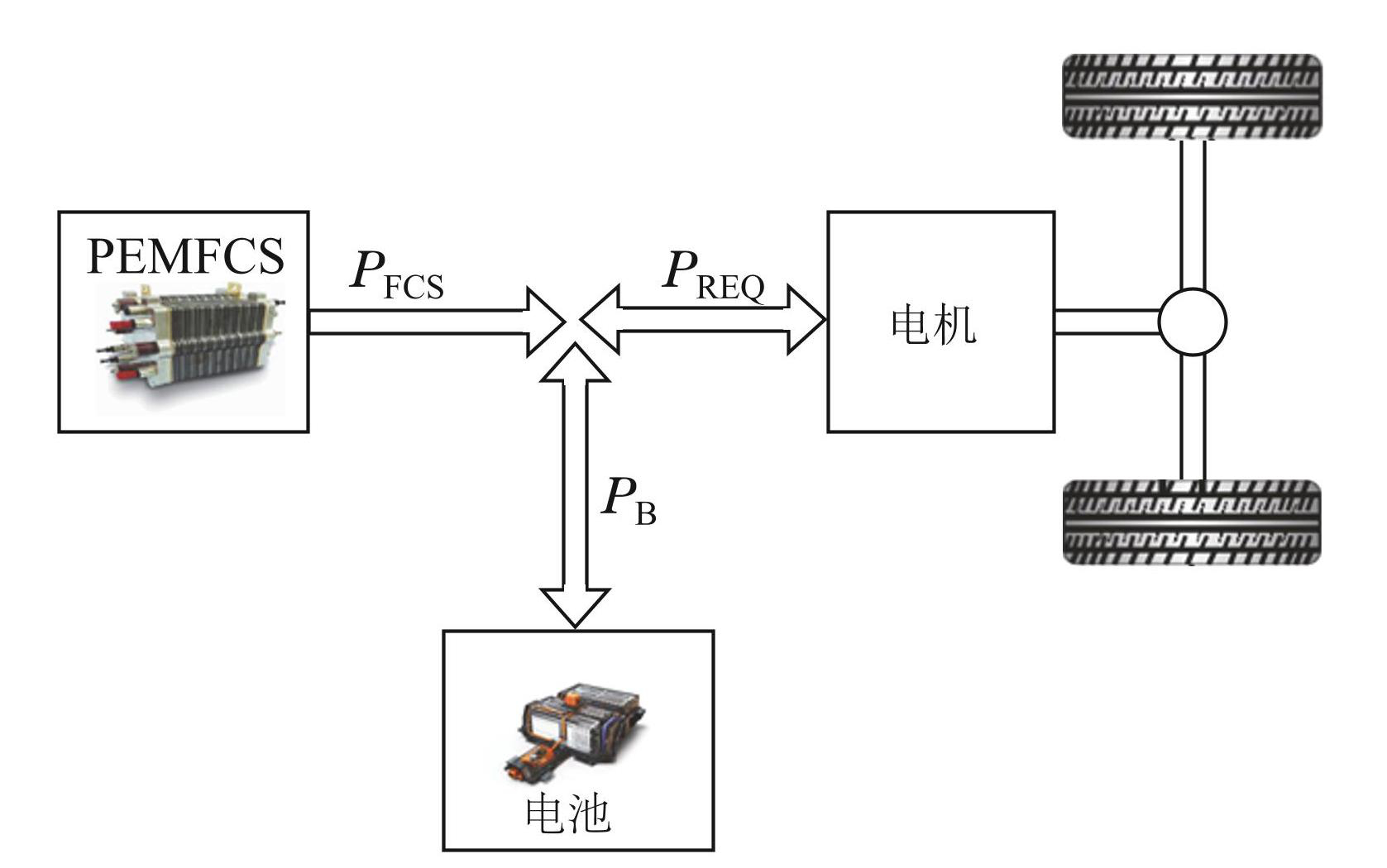
图1FCHEV架构

Fig.1FCHEV structure overview

正FCS功率P_FCS和电池功率P_B（放电时为正或充电时为负）连接到电气总线，以提供功率需求P_REQ，功率平衡应满足以下等式:

P_{F C S} (k) + P_{B} (k) = P_{R E Q} (k) .

(1)

如果功率要求P_REQ可以预先知晓，则只需要定义变量P_FCS和P_B中的一个. 为了使总燃料消耗最小化，这里选择变量P_REQ

作为决策变量. 考虑到不同的情况（充电或放电）和附件的能耗，每个采样点的电池能量应满足

E (k + 1) = E (k) - R (P_{B} (k)) \cdot T_{s},

(2)

其中: E（k）是存储在电池中的能量; T_s是采样时间; R（P_B（K））是指在P_B（K）的不同情况下提供给电气总线或从电气总线提供给电池的净功率; P_B（K）和 R（P_B（K））之间的关系可通过台架测试系统上的测量结果或通过电池模型的计算来获得. 由于P_FCS被选择为决策变量，因此式（2）可表示为FCS功率的函数，即

\begin{matrix} E (k + 1) = E (k) - R (P_{R E Q} (k) - \\ P_{F C S} (k)) \cdot T_{s} . \end{matrix}

(3)

燃料电池通过氢气和氧气之间的反应将化学能转化为电能. 燃料堆效率可根据以下公式计算:

η_{F C S} = \frac{P_{F C S}}{{\dot{m}}_{h} \cdot {L H V}_{H_{2}}}

(4)

FCS的效率与电流的关系和FCS功率与氢耗的关系如图2所示.

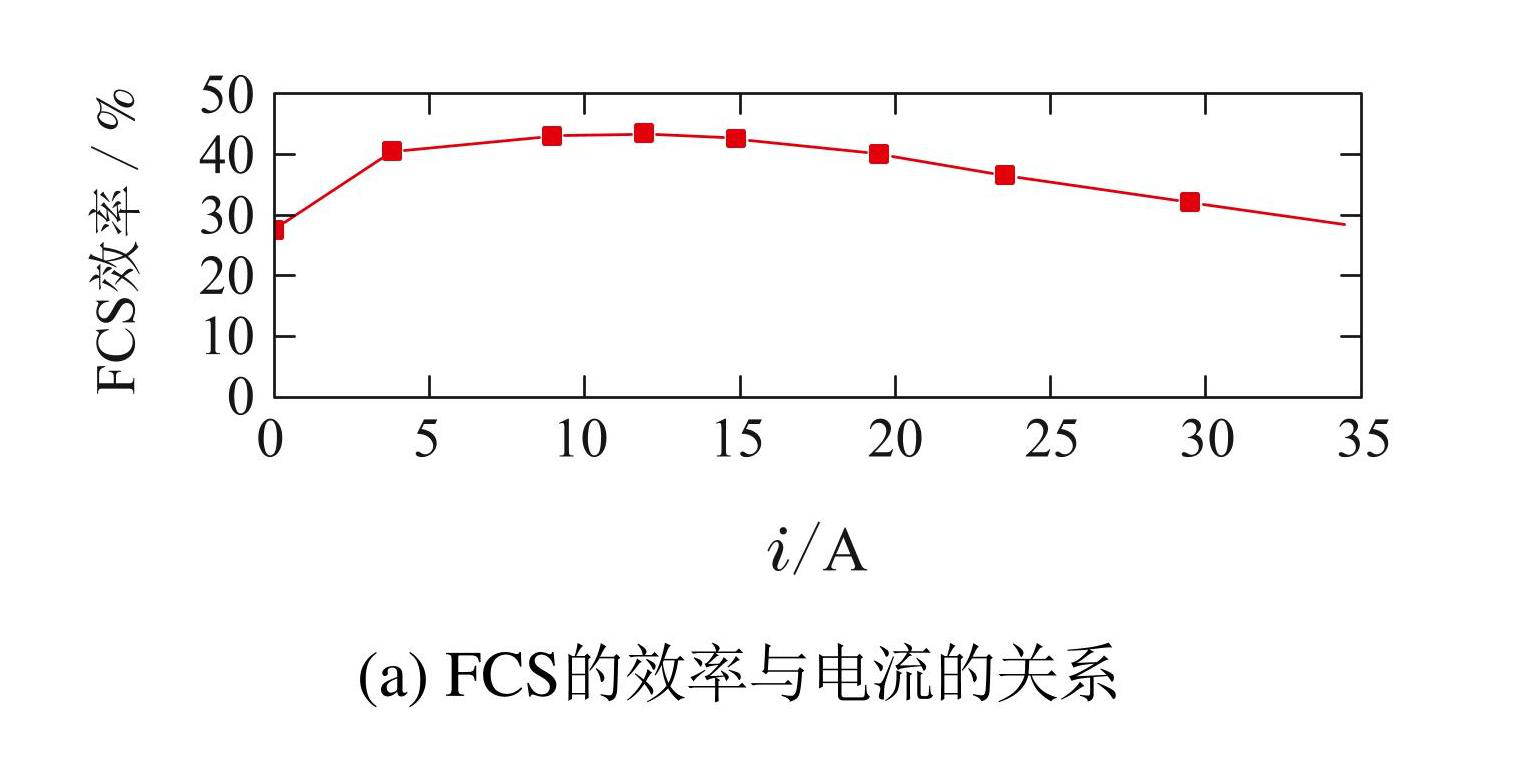
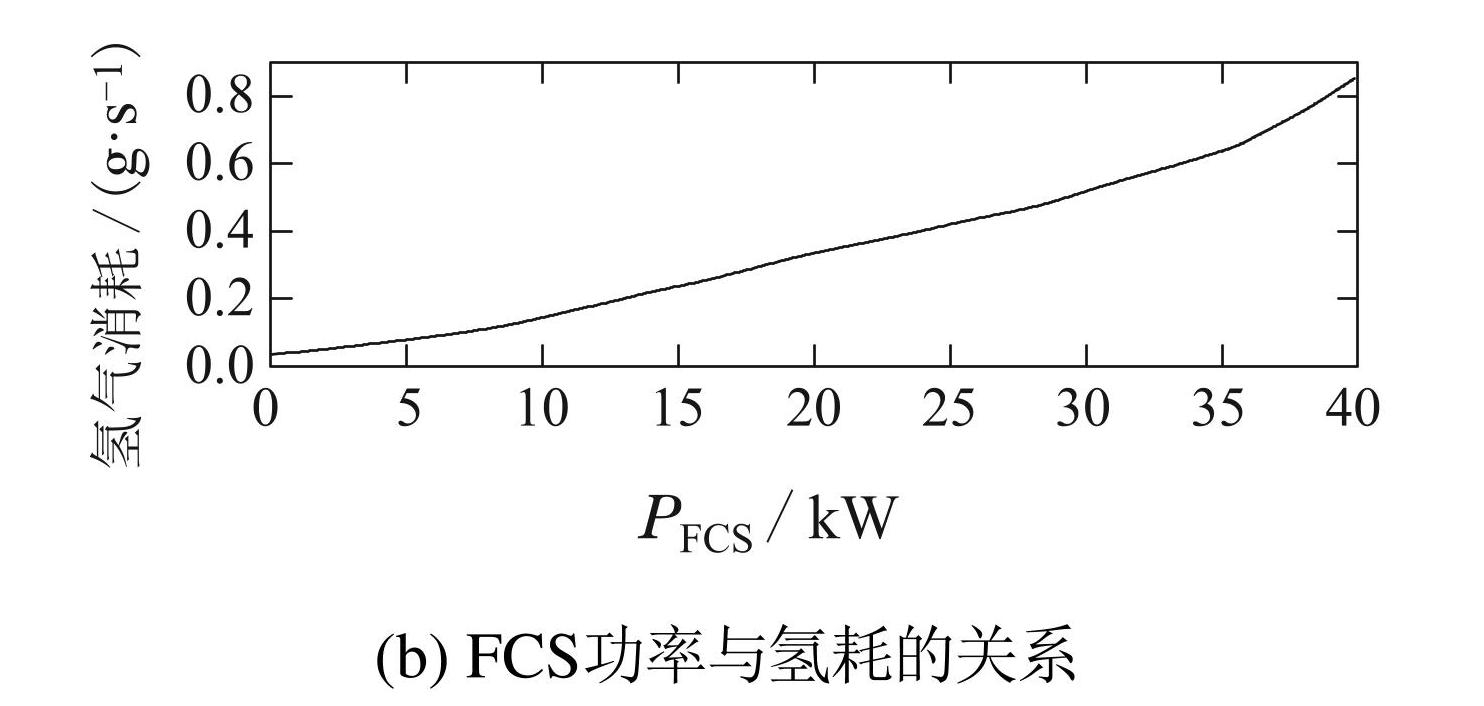
图2FCS的效率与电流的关系和FCS功率与氢耗的关系

Fig.2Efficiency vs current and power output vs fuel consumption of FCS

2.1 包含温度的电池模型

常用的电池模型如图3 ^[16] 所示.

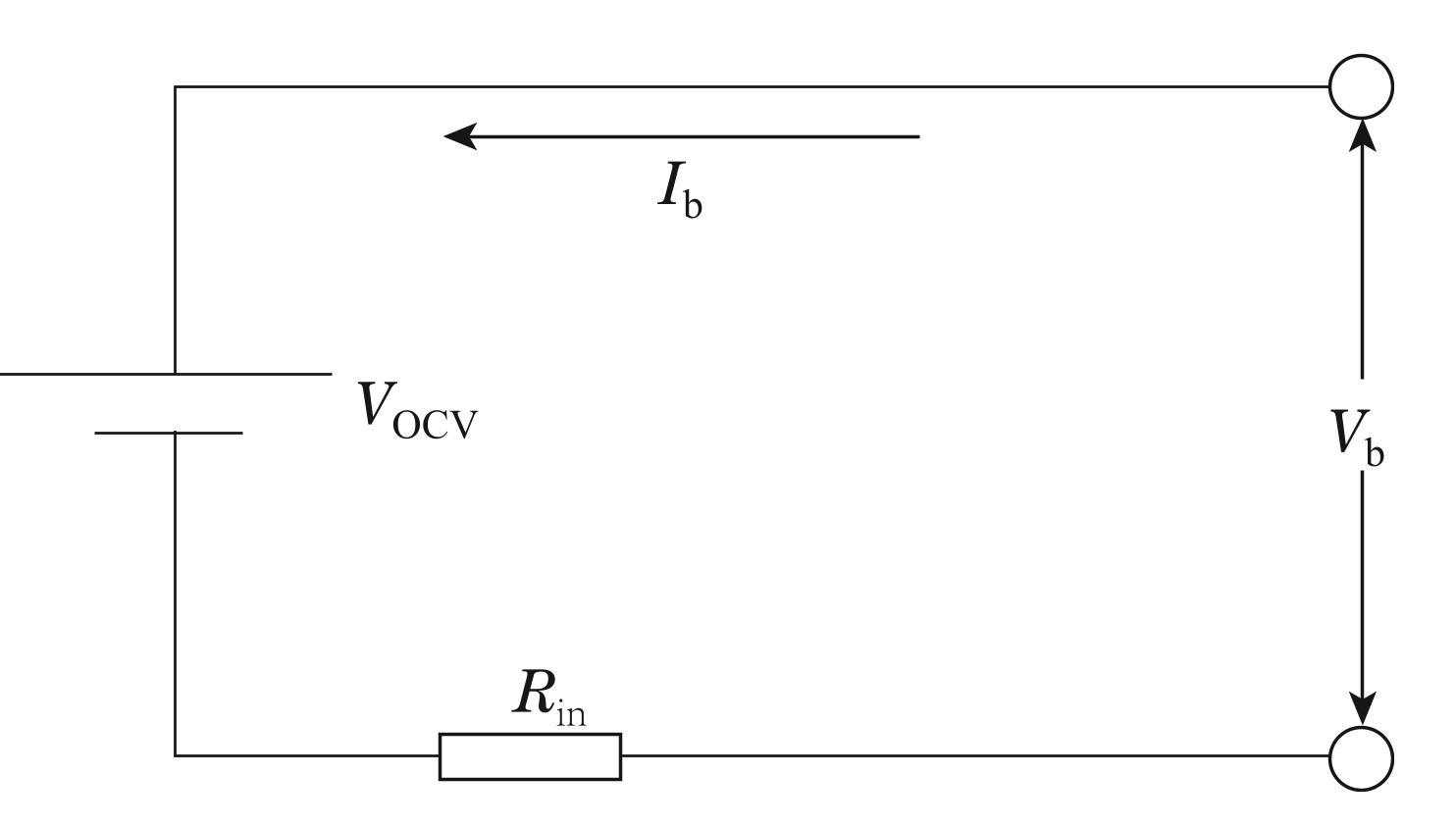
图3电池模型

Fig.3Battery model

电池的输出功率和开路电压可以通过以下方式计算:

V_{b} = V_{o c v} - R_{i n} \cdot I_{b},

(5)

P_{B} = V_{o c v} \cdot I_{b} - R_{i n} \cdot I_{b}^{2}

(6)

其中: V_ocv是电池的开路电压; I_b是电池的电流，根据上述公式，电池的电流与电池的输出功率的关系可以表示为

I_{b} = \frac{V_{o c v} - \sqrt{V_{o c v}^{2} - 4 P_{B} \cdot R_{i n}}}{2 R_{i n}} .

(7)

蓄电池的荷电状态（state of charge，SOC）可以通过以下方式计算:

S O C = {S O C}_{i n i t} - \frac{1}{Q_{c a p}} \int_{0}^{t} I_{b} d t

(8)

其中: SOC_init是电池的初始SOC值; Q_cap是以A · H 为单位的电池容量. 为了反映温度对电池输出功率的影响，内阻（在充电和放电情况下不同）可以被视为关于SOC，T和I_b的函数，即

R_{i n} = f (S O C, T, I_{b})

(9)

根据上述公式，进行实验，在不同温度和不同的 SOC值下的动力电池的开路电压的关系如图4（a）所示，同时图4（b）和图4（c）显示了不同SOC值和温度下动力电池充放电情况下的内阻.

图4考虑温度影响的电池模型

Fig.4Battery model considering temperature affection

电池的热模型可以描述如下:

\{\begin{matrix} \frac{d T_{c}}{d t} = \frac{T_{c} - T}{R_{i n} C_{i n}} + \frac{Q (t)}{C_{i n}}, \\ Q (t) = I_{b}^{2} R_{i n} (t), \end{matrix}

(10)

在式（10）中， T_c是电池圆柱形电池的温度，Q（t）是发热量，C_in是热容. 可以通过使用电池模型来获得 R（P_B（K））和P_B（K）之间的关系图. 图5反映25^◦C下 R（P_B（K））和P_B（K）关系的典型结果.

2.2 功率需求预测

以下部分详细介绍了基于统计方法的未来电力需求预测. 对于离线的FCHEV，影响未来功率需求的主要因素是驾驶员意图，驾驶员意图可以通过FCHEV 的状态来反映，例如当前加速度、减速度、车速和当前负载的状态. 因此，对于功率需求预测，车辆的当前状态向量可以在每个采样点的可能范围Φ （ij）内分配到一个有限离散族中，如下所示:

ϕ = [\begin{matrix} ϕ_{11} & ϕ_{12} & L & ϕ_{n_{c}} \\ ϕ_{21} & ϕ_{22} & L & ϕ_{n_{c}} \\ ϕ_{31} & ϕ_{32} & L & ϕ_{n_{c}} \\ M & M & L & M \\ ϕ_{i 1} & ϕ_{i 2} & L & ϕ_{n_{c}} \end{matrix}],

(11)

输入变量: u_i（k）= [a v P_c ∆²（filt（P_c））]，表示加速角（或负时的减速角）; v是车辆的当前速度; P_c是当前功率要求; ∆²表示二阶后向差分算子; filt（P_c）表示可以避免噪声和小负载峰值的低通滤波器. 在本文中，a的数量设置为12，6个用于加速，6个用于减速，v的离散数量设置为30（0∼60 km），因此P_c的数量为180，滤波器输入数量为12. 离散输入变量的数量将极大地影响预测精度.

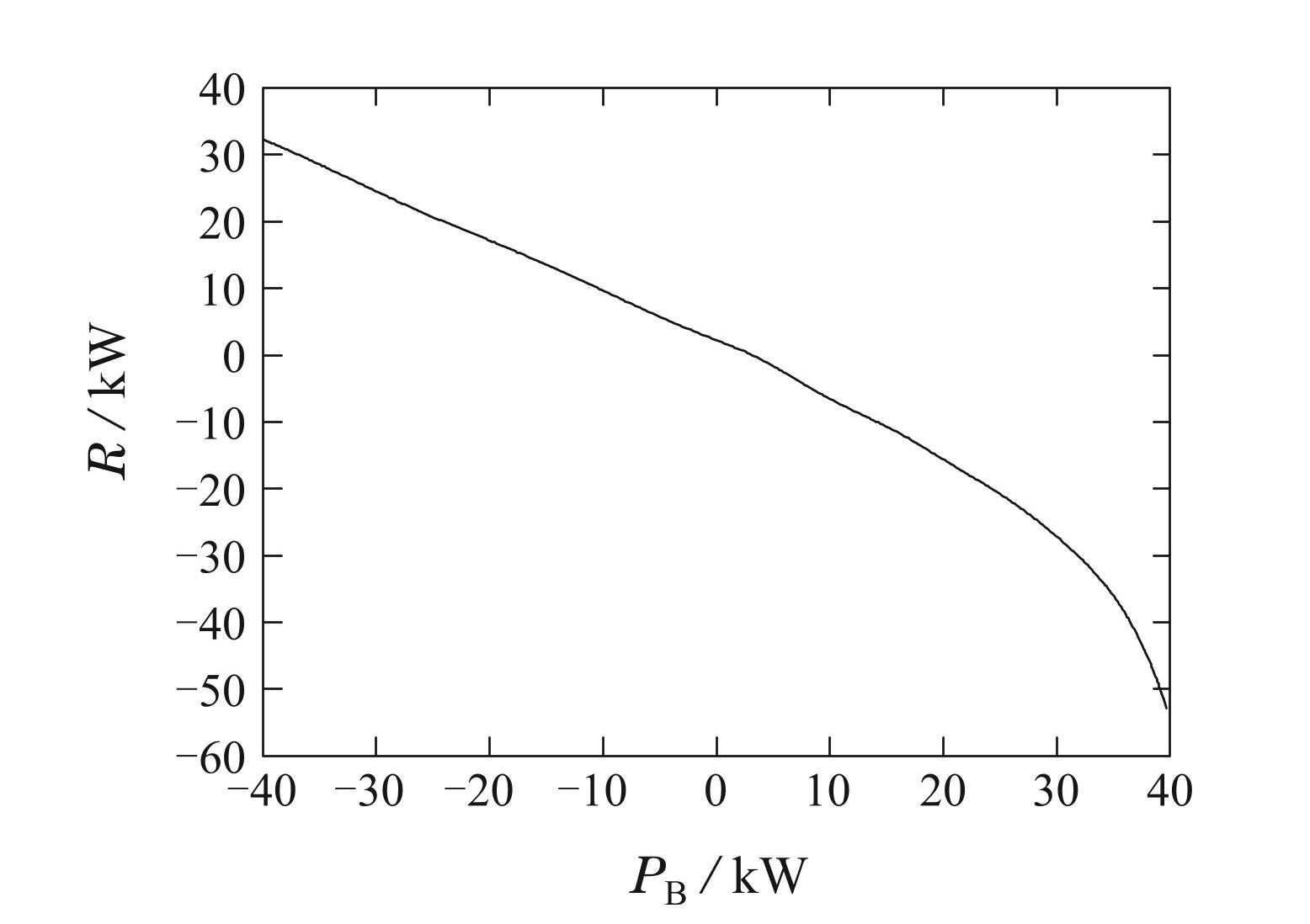
图525^◦C下R（P_B（K））和P_B（K）关系

Fig.5Relationship between R (P_B (K) ) and P_B (K) at 25^◦C

根据贝叶斯估计理论，首先通过实验根据测量数据计算先验概率和似然函数. 基于先验概率和似然函数，可以根据以下公式计算某一功率类Ψ_li在某一输入Φ （k）下的未来功率需求P（Ψ_hj |Φ（k））.

P (Ψ_{h j} ∣ Φ (k)) = \frac{P (Φ (k) ∣ Ψ_{h j}) P (Ψ_{h j})}{\sum_{j = 1}^{n_{c}} P (Φ (k) ∣ Ψ_{h j}) P (Ψ_{h j})},

(12)

上述功率需求的方法如图6所示. 未来功率需求的预测结果被确定为向量中每个预测步骤的最高功率类概率P（Ψ_hj |Φ（k）），即

P_{PREQ} = {[\begin{matrix} P_{PREQ, 1} P_{PREQ, 2} \dots P_{PREQ, n_{p}} \end{matrix}]}^{T} .

(13)

为了验证基于贝叶斯估计理论的功率需求方法，在测试台上进行了离线实验，结果如图7所示. 图7中的蓝线表示输入变量，红线是实际功率需求的测量结果，灰线是预测结果，预测范围设置为n_p = 50. 由此得出，可以获得相对准确的预测结果.

图6功率需求预测方法

Fig.6Power requirement prediction method

图7功率需求预测方法

Fig.7Power requirement prediction method

3 优化控制策略

3.1 目标函数

为了实现氢消耗的最佳经济性，目标函数定义为

J (P_{F C S}) = \sum_{k = 0}^{N} {\dot{m}}_{h} (P_{F C S} (k)) T_{s},

(14)

其中

{\dot{m}}_{h}

（g /s）是瞬时氢气流速. 氢气消耗受到许多不同操作条件的影响，如压力、温度、湿度等 ^[27-29] . 最佳燃油效率问题可以归结为

J (P_{F C S}) = \sum_{k = 0}^{N} {\dot{m}}_{h} (P_{F C S} (k)) T_{s},

s.t. \{\begin{matrix} P_{m i n} < P_{F C S} (k) < P_{m a x}, \\ P_{B - m i n} < P_{B} < P_{B - m a x}, \\ S O C (N) = S O C (0) + Δ {S O C}_{g a p}, \end{matrix}

(15)

其中:

P_{m i n} = m a x \{P_{F C S - m i n}, P_{R E Q} - P_{B - m a x} (E (k))\},

P_{m a x} = m i n \{P_{F C S - m a x}, P_{R E Q} - P_{B - m i n} (E (k))\},

P_FCS−min 和P_FCS−max是FCS的功率边界.

为了实现最佳的等效燃油经济性，使用最小原理作为控制算法. 综合考虑式（14）–（15）中的SOC值，使用拉格朗日系数λ（k）形成哈密顿方程H（k），即

\begin{matrix} H (k) = {\dot{m}}_{h} (P_{F C S} (k)) T_{s} - λ (k + 1) [E (k) - \\ R (P_{R E Q} (k) - P_{F C S} (k)) \cdot T_{s}] . \end{matrix}

(16)

为了获得最佳轨迹中的瞬时P_FCS，应首先根据式（16）确定拉格朗日系数λ （k），即

\frac{\partial H (k)}{\partial E (k)} = - λ (k), k \in {0, N},

(17)

式（17）意味着，在最佳过程中，λ（k）应为常数值，假设λ （k）= λ_c，则可以在最小化H （k）的条件下计算 P_FCS，即

\begin{matrix} P_{F C S} (k) = a r g m i n \{{\dot{m}}_{h} (P_{F C S} (k)) T_{s} - \\ λ [E (k) - R (P_{R E Q} (k) - \\ P_{F C S} (k)) \cdot T_{s}]\} = \\ π (P_{R E Q} (k), λ_{c}), \\ P_{m i n} (k) ⩽ P_{F C S} (k) ⩽ P_{m a x} (k) . \end{matrix}

(18)

为了获得适当λ_c，考虑到式（5）中的约束条件，应首先定义∆SOC_gap. 考虑到SOC值的近似值

S O C = \frac{E}{E_{m a x}},

(19)

其中: E是存储在电池中的当前能量; E_max是电池的最大能量; ∆E可以使用式（2）和式（18）进行计算，即

Δ E = T_{s} \sum_{k = 0}^{N} R [P_{R E Q} (k) - Π (P_{R E Q} (k), λ_{c}) .

(20)

综合考虑式（19）–（20），∆SOC_gap可被视为λ_c的函数，即

\begin{matrix} Δ {S O C}_{g a p} = f (λ_{c}) = \frac{T_{s}}{E_{m a x}} \sum_{k = 0}^{N} R [P_{R E Q} (k) - \\ Π (P_{R E Q} (k), λ_{c})] . \end{matrix}

(21)

在实际应用寻找λ_c的过程中，为了降低计算复杂度，将功率需求P_R（k）的实际范围划分为第m个区间，每个区间的功率需求可以用平均功率P_R−m表示，因此，可以根据变换后的方程计算λ_c，

\begin{matrix} Δ {S O C}_{g a p} = \frac{T_{s}}{E_{m a x}} \sum_{m = 1}^{M} R [P_{R E Q} (m) - \\ Π (P_{R E Q} (m), λ_{c})] . \end{matrix}

(22)

图8进一步描述了近似方法，当功率需求被划分为40个级别时，平均m = 40，用该近似得到的λ_c为 3.5 × 10⁻⁵ .

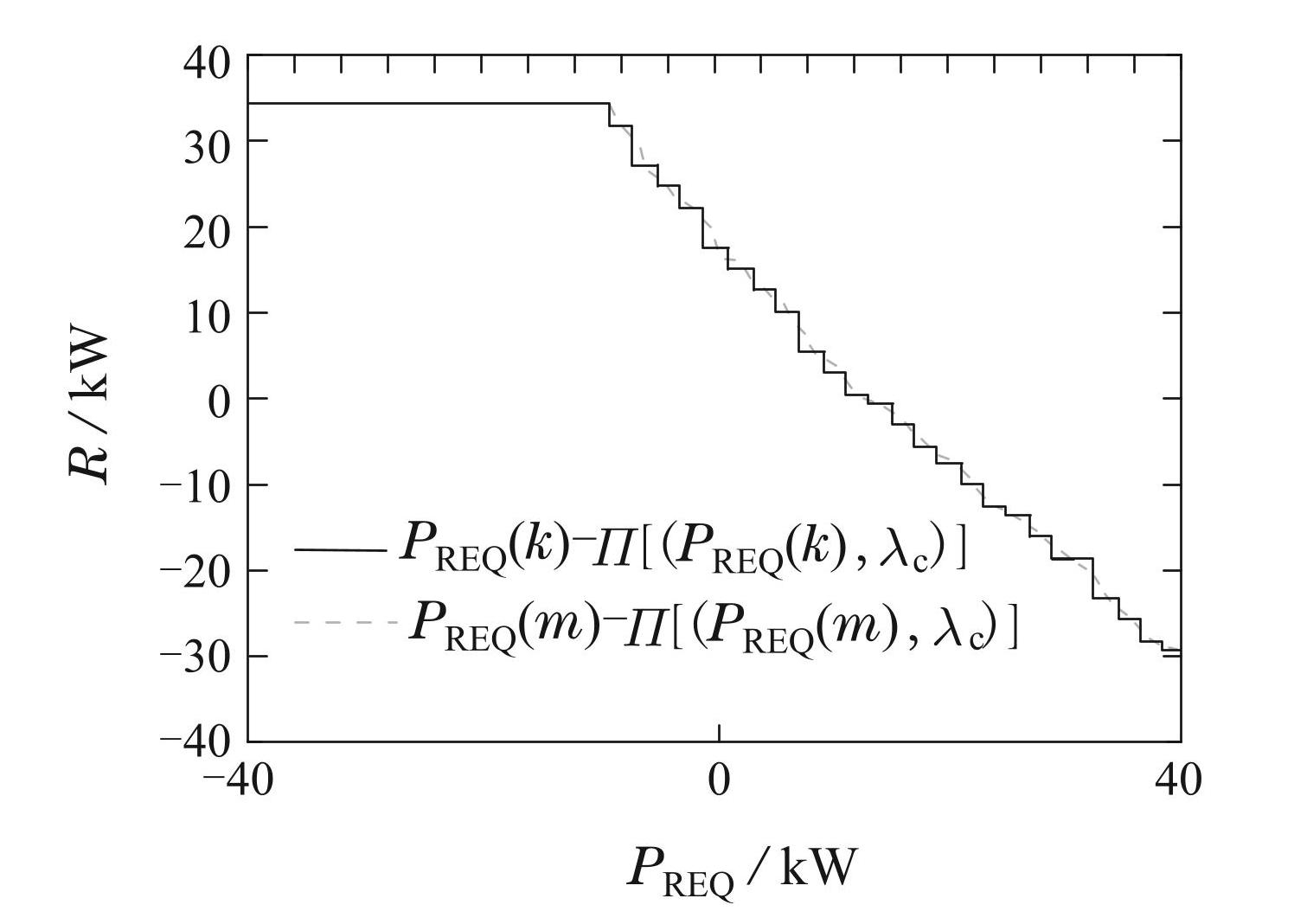
图8R的直接计算法与近似值的比较

Fig.8Comparison of direct calculation of R and its approximation

计算∆SOC_gap与方法（21）–（22）的比较结果如图9 所示.

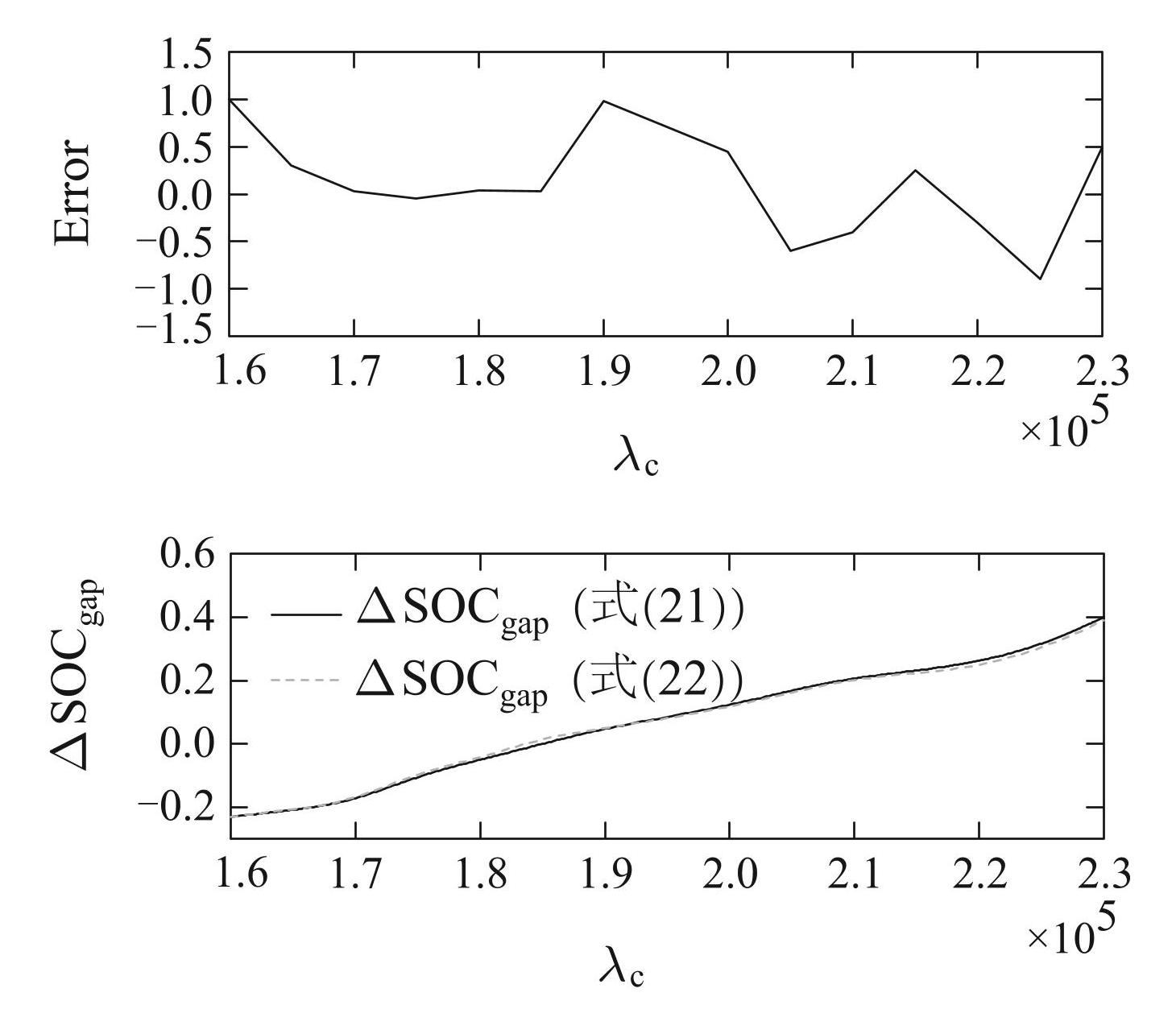
Fig.9直接计算法和近似法的包含误差的比较

Fig.9Comparison of direct calculation of R and its approximation

3.2 实时控制

如前一节所述，估计λ_c导致动力传动系的功率分配，以实现最佳等效燃油经济性. ∆SOC_gap可以预先精确定义，实时控制策略的主要思想是根据 ∆SOC_gap和功率要求定期找到λ_c. 实时控制方法如图10所示.

根据等式（12），不必事先知道具体的功率需求，但应该在一开始就知道未来的功率需求分布，这意味着应该首先知道总的驱动条件. 对于驾驶情况的连续性，可以根据等式（12）计算过去的功率需求，因此，可以认为未来的功率需求分布与最后N个样本上的过去分布相同. P_v（k），k = [i + 1 · · · i + N]的未来分布n_i，i = 1，· · ·，M相同，P_v（k），k = [i− N · · · i]的未来分配 n_f_i，i = 1，· · ·，M. 在样本 i 的时刻，一旦确定 ∆SOC_gap，就可以使用式（22）的解来求出系数，因此实时控制策略的主要步骤可以总结为

1）最后N个样本的过去功率需求分布的计算;

2）未来电力需求预测;

3）根据式（22），基于SOC（∆SOC_gap）估算系数λ_c;

4）根据式（18）计算功率分布，以实现最佳等效燃油经济性.

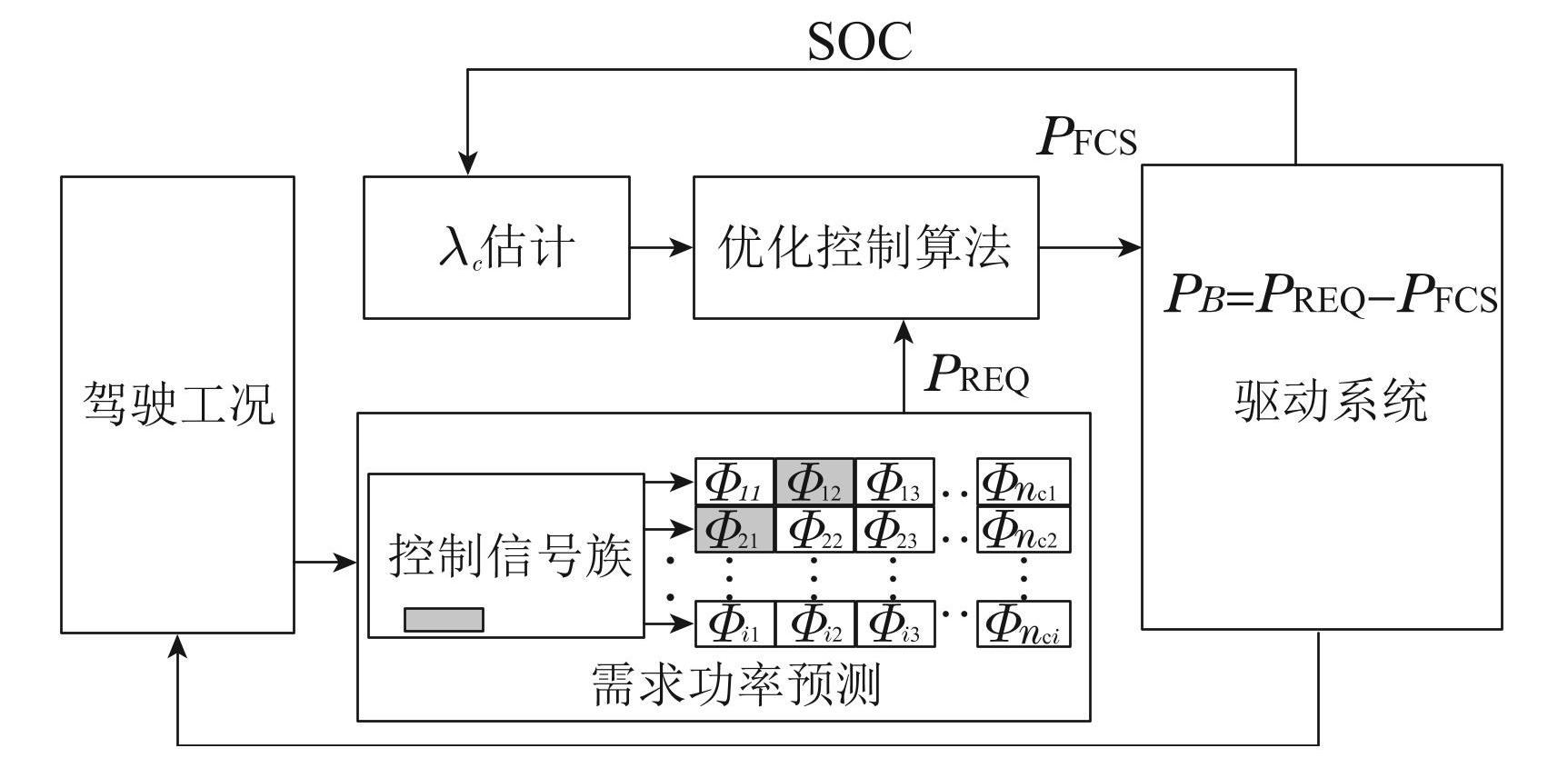
图10实时控制策略

Fig.10Real time control strategy

4 仿真和实验验证

为了验证所提出的实时控制策略并模拟FCHEV 的功率流，使用测试台来检查所提出的控制策略的性能. 硬件在环（hardware-in-the-loop，Hil）系统的结构如图11所示. 试验台的详细参数如表1所示. 其中DC– DC为直流–直流转换器.

图11FCS 测试台及其结构

Fig.11FCS test bench and its structure

对于相同的驾驶循环和相同的功率要求，通过固定∆SOC_gap值，SOC 值变化对拉格朗日系数的影响如图12 所示. 如果 SOC 值的变化较大（亮线，∆SOC_gap = −28%），这意味着电池有更深的放电，则用所提出的方法发现的λ_c较小（λ_c = 1.7×10⁻⁵），当SOC值变化较小（暗线，∆SOC_gap =+12%）时，λ_c将更大（λ_c = 2.9 × 10⁻⁵），λ_c越小，氢消耗将越少.

表1控制测试台参数

Table1Specifications for control testbench

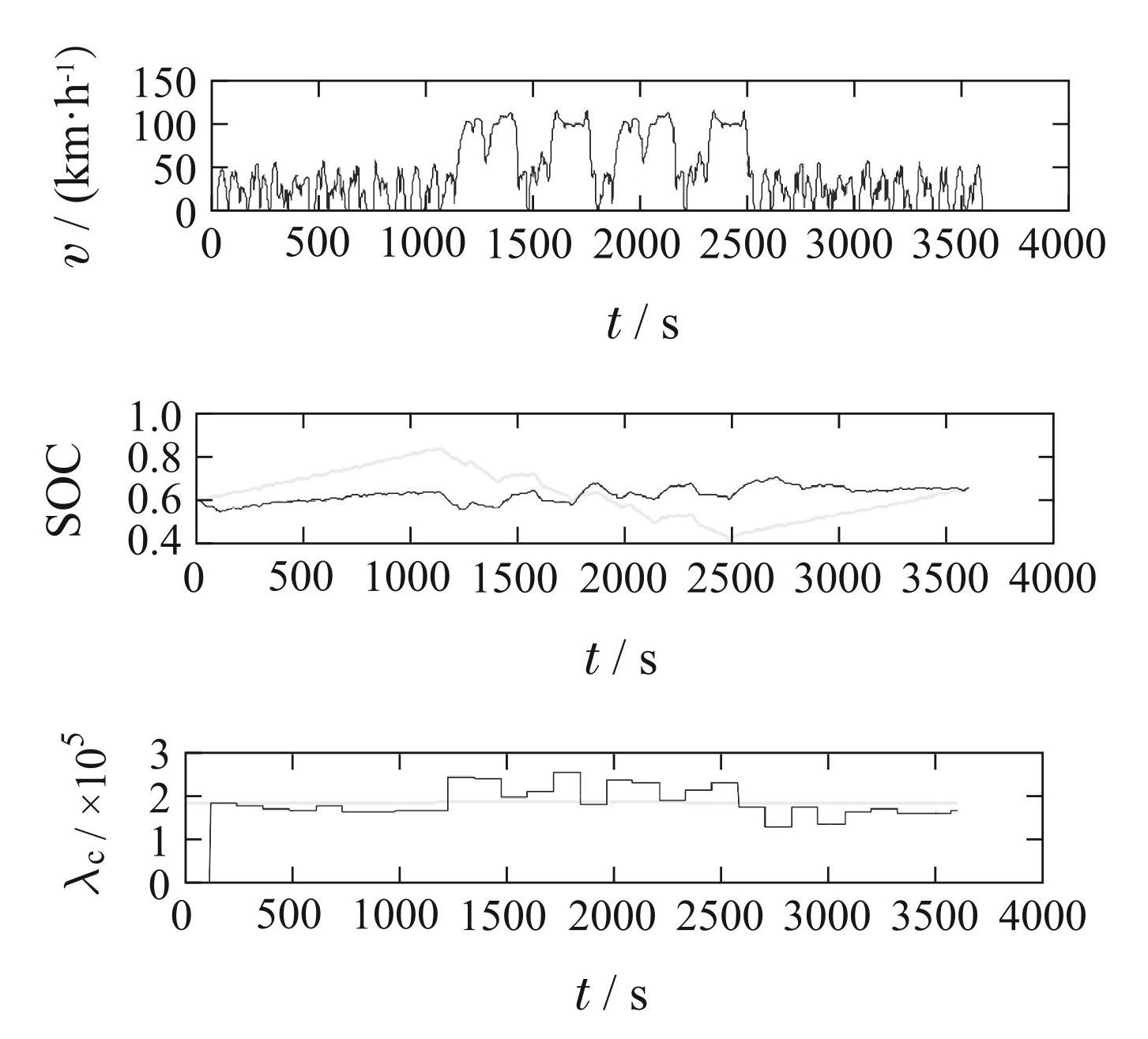
图12SOC变化对λ_c的影响

Fig.12Influence of SOC variation on λ_c

仿真结果如图13所示. 将保持λ_a不变的离线优化与所提出的控制策略进行了比较. 对于所提出的控制策略，最终SOC设置为60%，T_s = 1 s，样本数N=120. 这两个优化实现了良好的等效燃油消耗和SOC值调节. 对于相同的∆SOC_gap = 5%，在拟议策略情况下和比较情况下的氢气消耗量分别为 1.56 kg/100 km 和 1.61 kg/100 km. 与离线优化相比，油耗提高了3.5%. 优化过程中的系数λ_c仅略有变化.

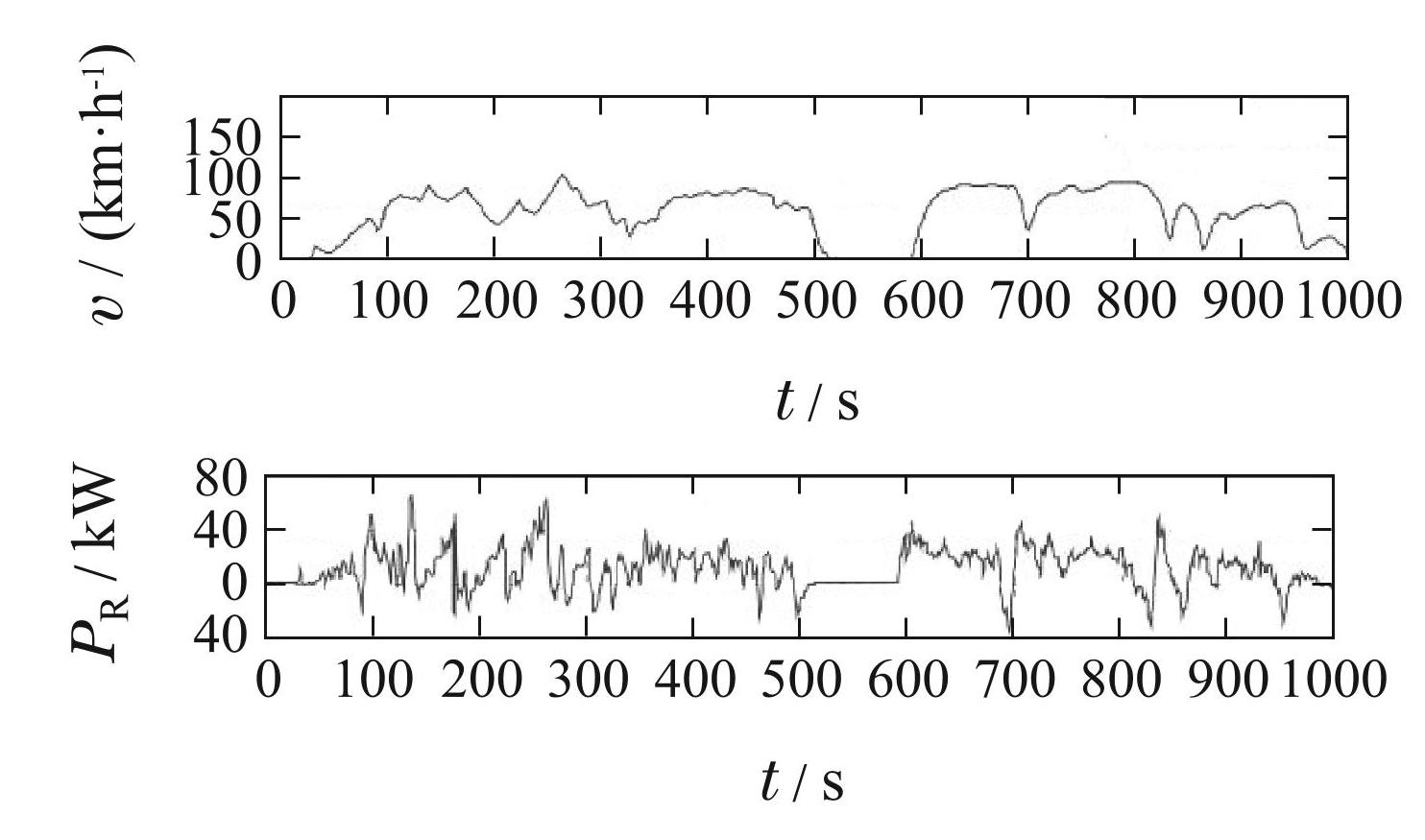
图13建议策略和对比策略的硬件在环实验结果

Fig.13Hil experiment results of the proposed control strategy and the contrast strategy

为了进一步验证所提出的控制策略，使用混合驱动循环进行验证. SOC 值被调整为0.7，样本数量被调整为 N = 240（4 min），样本步长仍然为 T_s = 1 s. 在 Hil 验证中，可以根据驾驶周期修改相关参数. 结果如图14所示. λ_c 在所提出的控制策略中的作用是清楚的，高速级将使用高值的λ_c. SOC 值变化间隙 ∆SOC_gap保持在 4.9%以下的可接受范围内，氢消耗量为1.69 kg/100 km.

图14所提出控制策略实验结果

Fig.14Experiment results of the proposed control strategy

将所提出的控制策略在离线情况、在线情况和最小损失策略（loss minimum strategy，LMS）下的氢气消耗量进行了比较，如图15所示. 选择LMS作为比较的原因在于，LMS中的SOC值是根据灵敏度分析设置的，并根据仿真模型进行集中调整，这使得结果尽可能合理 ^[30] . 可以看出，当估计的SOC值为负时，3种控制策略的差异很小，但当SOC值为正时，差异明显增加. 原因在于，如果SOC值为负，功率主要来自电池，则所提出的控制策略对氢消耗的影响较弱，但当SOC值为正，功率主要来源于FCS时，则所建议的控制策略将对氢消耗产生较强影响. 在SOC值为10% 的情况下，试验台的测试结果比实际实验结果节省2%，实验结果比LMS控制策略节省5%.

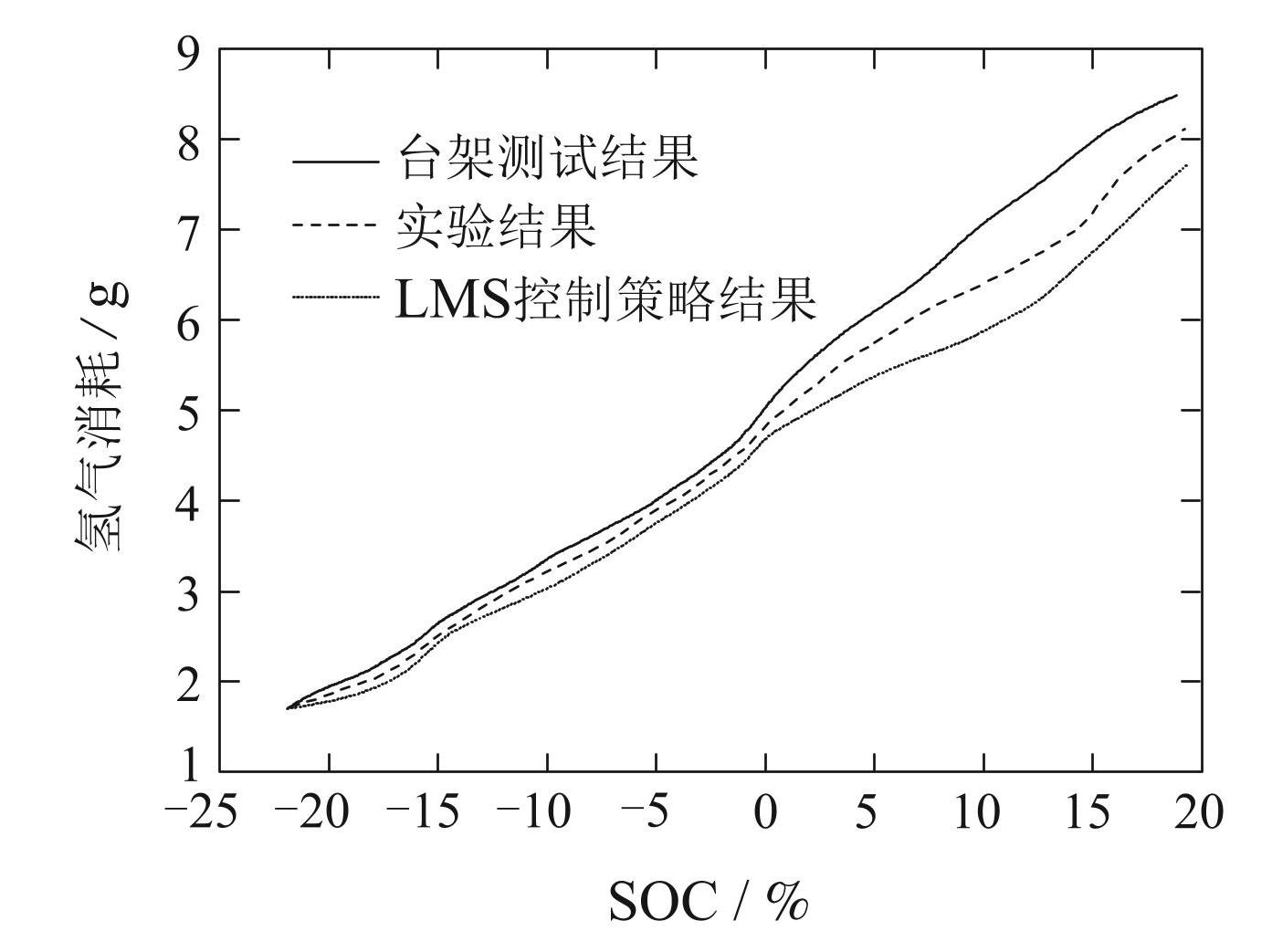
图15氢消耗与SOC值之间的关系

Fig.15Relationship between hydrogen consumption and SOC balance

由于所提出的控制策略考虑了温度对电池的影响，因此比较了不同控制策略下电池的温度，如图16所示.

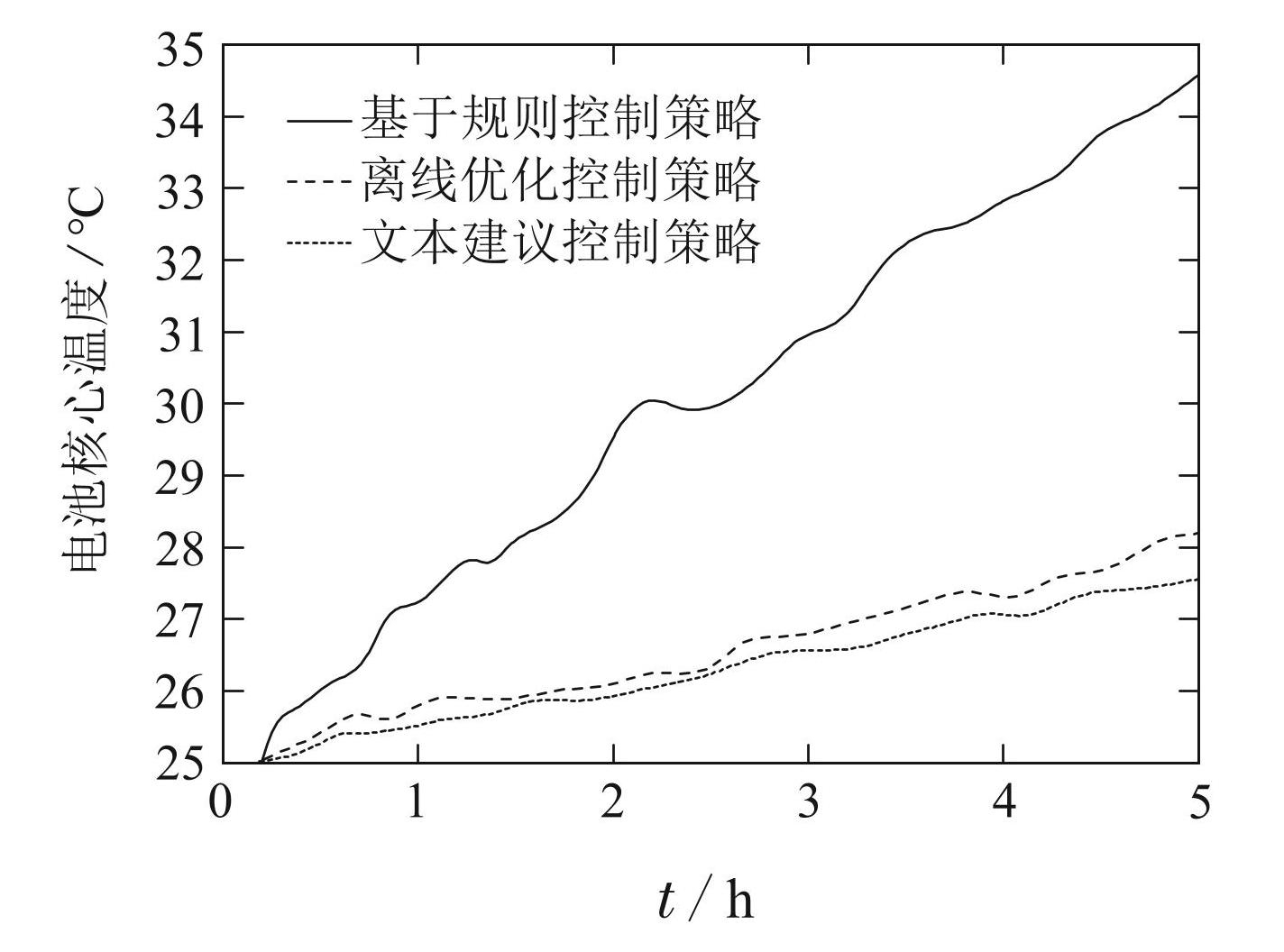
图16不同控制策略下电池温度

Fig.16Battery temperature under different control strategies

如图16所示，当根据基于规则的控制策略将功率需求分配给电池时，由于没有考虑温度的影响，温度会急剧上升. 离线优化控制和所提出的优化控制几乎具有相似的温度曲线. 相反，结果表明，离线优化的核心温度略高于所提出的最优，因为后者使用一种方法来找到合适的λ_c，而离线优化使用一个常数λ. 这将有助于减少氢气消耗并延长电池寿命.

5 结论

基于能量流平衡和最小原理，提出了一种有效的实时控制策略，以实现良好的等效燃油经济性. 针对考虑电池热模型的燃料电池混合动力汽车配置，提出了基于MPC的能量管理策略框架，并提出了一种新的基于贝叶斯统计方法的功率需求预测方法. 为了验证所提出的控制策略，进行了仿真和Hil实验. 结果表明，所提出的控制策略可以将氢气消耗量至少降低4%. 此外，电池温度在电池老化中起着重要作用. 比较了不同控制下的燃料电池堆温度，提出的控制策略可以有效降低燃料电池堆温度并降低油耗.

事实上，FCS的性能在很大程度上取决于其温度，因此可以通过考虑温度对氢气消耗的影响来进一步改进所提出的控制策略.

FLADUN A, SCHOLZ H, BERGER O. Evaluating the influence of requirements in fuel cell system design using design requirement maps. Fuel Cells,2021,21(4):347-362.

TANG Z P, HUANG Q A, WANG Y J,et al. Recent progress in the use of electrochemical impedance spectroscopy for the measurement,monitoring,diagnosis and optimization of proton exchange membrane fuel cell performance. Journal of Power Sources,2020,468(9):1134-1148.

WANG X R, MA Y, GAO J,et al. Review on water management methods for proton exchange membrane fuel cells. International Journal of Hydrogen,2021,46(22):12206-12229.

OUDDAH N, ADOUANE L, ABDRAK R. From offline to adaptive online energy management strategy of hybrid vehicle using Pontryagin’s minimum priciple. International Journal of Automotive Technology,2018,19(3):571-584.

KANDIDAYEI M, MACIAS A, KHALATBARISOLTANI A,et al. Benchmark of proton exchange membrane fuel cell parameters extraction with metaheuristic optimization algorithms. Energy,2019,183:912-925.

BRESSEL M, HILAIRET M, HISSEL D,et al. Extended Kalman filter for prognostic of proton exchange membrane fuel cell. Appl Energy,2016,164:220-227.

LEE H, JEONG J, PARK Y,et al. Energy management strategy of hybrid electric vehicle using battery state of charge trajectory information. International Journal of Precision Engineering and Manufacturing-Green Technology,2017,4(1):79-86.

HU J Y, LI J Q, HU Z Y,et al. Power distribution strategy of a dualengine system for heavy-duty hybrid electric vehicles using dynamic programming. Energy,2021,215(1):376-389.

PAPAMARKOU T, MIRA A, GIROLAMI T. Zero variance differential markov chain monte carlo algorithms. Bayesian analysis,2014,9(1):97-127.

KHEIRANDISH A, SHAFIABADY N, DAHARI M,et al. Modeling of commercial proton exchange membrane fuel cell using support vector machine. International Journal of Hydrogen,2016,41(26):11351-11358.

MAYNE D Q, RAELINGS J B, RAO C V,et al. Constrained model predictive control: Stability and optimality, Automatica,2000,36(6):789-814.

PAN X B. Output feedback robust MPC based on off-line observer for lpv systems via quadratic boundedness. Asian Journal of Control,2017,12(3):1641-1653.

SHUO Z, XIONG R, SUN F C. Model predictive control for power management in a plug-in hybrid electric vehicle with a hybrid energy storage system. Applied Energy,2017,185(3):1654-1662.

KIM N, CHA S, PENG H. Optimal control of hybrid electric vehicles based on Pontryagin’s minimum principle. IEEE Transactions on Control Systems Technology,2010,19(5):1279-1287.

YUAN Z, WANG W Q, WANG H Y,et al. Parameter identification of PEMFC based on convolutional neural network optimized by balanced deer hunting optimization algorithm. Energy Report,2020,6:1572-1580.

LARIBI S, MAMMAR K, SAHLI Y,et al. Analysis and diagnosis of PEM fuel cell failure modes(flooding & drying)across the physical parameters of electrochemical impedance model: Using neural networks method. Sustainable Energy Technologies and Assessments,2019,34:35-42.

ATTIA A, HANG M, AHMED M. Semi-empirical PEM fuel cells model using whale optimization algorithm. Energy Conversion and Management,2019,201:1879-1892.

FATHY A, ELAZIA M, ALHARBI AG. A novel approach based on hybrid vortex search algorithm and differential evolution for identifying the optimal parameters of PEM fuel cell. Renew Energ,2020,146:1833-1845.

JAHNKE T, FUTER G, LATZ A,et al. Performance and degradation of proton exchange membrane fuel cells: State of the art in modeling from atomistic to system scale. Journal of Power Sources,2016,304:207-233.

XIONG R, CAO J, YU Q. Reinforcement learning-based real-time energy management for hybrid energy storage system in the plug-in hybrid electric vehicle. Applied Energy,2018,211:538-548.

BLOOM I, COLE B W, SOHN J J,et al. An accelerated calendar and cycle life study of Li-ion cells. Journal of Power Sources,2001,101(2):238-247.

LIU H, MI X, LI Y. Smart multi-step deep learning model for wind speed forecasting based on variational mode decomposition,singular spectrum analysis, LSTM network and ELM. Energy Conversion and Management,2018,1(159):54-64.

MORANDO S, JEMEI S, HISSEL D,et al. A nova method applied to proton exchange membrane fuel cell ageing forecasting using an echo state network. Mathematics and Computers in Simulation,2017,1(131):283-294.

SIMMONS K, GUEZENNEC Y, ONORI S. Modeling and energy management control design for a fuel cell hybrid passenger bus. Journal of Power Sources,2014,246(3):736-746.

DING K, ZHU M F, HAN Z,et al. Momentum-species-heatelectrochemistry distribution characteristics within solid oxide fuel cell stack with complex inter-digital fuel channels. Ionics,2020,26(9):4567-4578.

PIANKO-OPRYCH P, HOSSEINI S M, JAWORSKI Z. Model development of integrated CPOx reformer and SOFC stack system. Polish Journal of Chemical Technology,2016,18(4):41-46.

PROKOP T A, BERENT K, MOZDZIERZ M,et al. A threedimensional microstructure-scale simulation of a solid oxide fuel cell anode-the analysis of stack performance enhancement after a longterm operation. Energies,2019,12(24):747-751.

HWANG J J, CHANG W R, CCHAO C H,et al. Mass transports in an air-breathing cathode of a proton exchange membrane fuel cell. Journal of Fuel Cell Science and Technology,2009,6(4):1234-1246.

JAVED K, GOURIVEAU R, ZERHOUNI N,et al. Prognostics of proton exchange membrane fuel cells stack using an ensemble of constraints based connectionist networks. Journal of Power Sourcess,2016,30(324):745-57.

TAO F Z, ZHU L L, FU Z M,et al. Frequency decoupling-based energy management strategy for fuel cell/battery/ultra capacitor hybrid vehicle using fuzzy control method. IEEE Access,2020,8(4):166491-166502.