欢迎访问《控制理论与应用》期刊网站！

基于MPC迭代学习的四旋翼无人机轨迹跟踪控制

doi: 10.7641/CTA.2025.40310

王娟^1,2 ，赵成璟³ ，杨智杰¹

1. 沈阳建筑大学电气与控制工程学院辽宁沈阳 110168

2. 中国科学院沈阳自动化研究所机器人学国家重点实验室辽宁沈阳 110169

3. 大连华锐重工股份有限公司辽宁大连 116013

基金项目: 机器人学国家重点实验室开放基金项目(2024–O22), 辽宁省自然科学基金项目(2023–MS–224)资助

详细信息

作者简介

王娟副教授,目前研究方向为机器人智能控制和多模态切换控制等,E-mail: wangjuanneu@163.com;

赵成璟硕士,软件工程师,目前研究方向为四旋翼无人机轨迹跟踪,E-mail: 910453195@qq.com;

杨智杰硕士研究生,目前研究方向为多智能体协同控制,E-mail: finallords@163.com.

通信作者

王娟，E-mail: wangjuanneu@163.com.

Trajectory tracking control of quadcopter UAV based on MPC iterative learning

WANG Juan^1,2 ， ZHAO Cheng-jing³ ， YANG Zhi-jie¹

1. School of Electrical and Control Engineering, Shenyang Jianzhu University, Shenyang Liaoning 110168 , China

2. State key Laboratory of Robotics, Shenyang Institute of Automation, Chinese Academy of Sciences, Shenyang Liaoning 110169 , China

3. Dalian Huarui Heavy Industry Group Co., Dalian Liaoning 116013 , China

Funds: Supported by the State Key Laboratory of Robotics Open Foundation (2024–O22) and the Liaoning Provincial Natural Science Foundation (2023– MS–224).

摘要

本文研究四旋翼无人机在外部扰动影响下的轨迹跟踪问题, 提出一种基于MPC的迭代学习方法. 首先, 设计MPC控制器作为四旋翼无人机系统的反馈控制器, 且在MPC反馈环节引入预测误差进行反馈矫正. 在此基础上, 设计迭代学习控制器作为无人机系统的前馈控制器; 采用双曲正切函数对迭代学习控制器的学习增益进行优化, 减少迭代次数的同时能够提高轨迹跟踪精度. MPC反馈和迭代前馈的复合控制能够很好的克服外部扰动带来的影响, 实现无人机高精度的轨迹跟踪. 最后, 通过仿真验证本文所提方法的可行性和有效性, 通过实验对比, 本文设计的方法跟踪精度更高, 具有强鲁棒性.

关键词

模型预测控制 / 迭代学习 / 四旋翼无人机 / 轨迹跟踪

Abstract

This paper investigates the trajectory tracking problem of quadcopter UAV under external disturbances and proposes an iterative learning control method based on MPC. Firstly, design the MPC controller as the feedback controller of the quadcopter UAV system, and introduce prediction error into the MPC feedback loop for feedback correction. On this basis, the iterative learning controller is designed as the feedforward controller of the quadcopter UAV system. Employing hyperbolic tangent function optimizes the learning gain of the iterative learning controller, which can reduce the number of iterations and improve trajectory tracking accuracy. The composite control of MPC feedback and iterative feedforward can effectively overcome the impact of external disturbances and achieve high-precision trajectory tracking of UAV. Finally, the feasibility and effectiveness of the proposed method are verified through the simulation. By the experimental comparison, the method designed in this paper has higher tracking accuracy and strong robustness.

Keywords

model predictive control / iterative learning / quadcopter UAV / trajectory tracking

1 引言 2 问题描述 3 控制方案 4 基于MPC迭代学习系统稳定性分析 5 仿真实验及分析 6 结束语

1 引言

四旋翼无人机可以空中悬停，自由起降，并具有灵活性好、造价低和机动性强等特点 ^[1] . 四旋翼无人机是一个具有欠驱动、强耦合、非线性等特性的系统 ^[2] .四旋翼无人机如何在未知干扰情况下完成对期望轨迹的渐进跟踪，具有重要的理论研究意义和应用价值. 对于四旋翼无人机轨迹跟踪控制问题，已涌现出很多控制方法，如PID控制 ^[3-4]、模型预测控制 ^[5]、滑模控制 ^[6-7]、迭代学习控制 ^[8] 和强化学习方法 ^[9] 等.

MPC算法是一种基于数据和数学模型的方法，可用于对未知数据进行预测; 其优点在于其高准确性、快速性、可扩展性、可解释性和适应性 ^[10] . 模型预测控制能够处理非线性、约束和不确定等复杂的工程问题，因此很多研究人员将MPC算法应用于四旋翼无人机的系统控制. 文献 ^[11] 提出了无偏移MPC技术，解决了无人机存在各种不确定性和外部干扰的情况下的轨迹跟踪控制问题. 文献 ^[12] 考虑了无人机在时变信道下的跟踪控制问题，并提出了基于几何空间一致的MPC控制方法. 进一步，文献 ^[13] 提出轮廓MPC控制算法，实现了垂直起降无人机的高速轨迹跟踪. 文献 ^[14] 将高斯回归与MPC相结合，通过高斯回归补偿动力学误差，提出了在线高斯模型驱动的MPC控制方法. 文献 ^[15] 提出了结合干扰观测器的多无人机MPC 控制策略. 最近，基于滑模的MPC无人机跟踪控制方法被提出 ^[16] .

迭代学习控制（iterative learning control，ILC）具有较低的模型依赖、较强的鲁棒性以及较高的控制精度，这种控制方法适用于具有重复运动性质的被控对象，能够以非常简单的方式处理不确定度较高的非线性强耦合问题. 无人机的迭代学习控制也取得了一些结果，文献 ^[17] 提出了基于迭代学习的无人机自抗扰控制方法; 进一步，文献 ^[18] 提出了基于平滑迭代学习的无人机轨迹跟踪控制方法; 文献 ^[19] 提出了基于点对点轨迹更新跟踪的无人机编队迭代学习控制方法; 文献 ^[20] 提出了无人机轨迹跟踪的鲁棒迭代学习控制策略.

众所周知，对于四旋翼无人机轨迹跟踪问题，系统的鲁棒性和跟踪精度一直备受关注. 四旋翼无人机的运动容易受到外部扰动（如风、气流等）的影响，这会影响到轨迹跟踪的精度，而上述单一的MPC和ILC无法实现无人机在外部扰动下的高精度跟踪. 针对外部扰动带来的不利影响，如何联合MPC和ILC的各自优势实现无人机高精度轨迹跟踪，这一问题亟待解决且具有一定的挑战性. 本文在 MPC 中引入误差补偿机制，在ILC中使用双曲正切函数优化迭代学习增益，提出基于MPC的迭代学习控制方法，能够实现无人机在具有外部扰动的情况下的高精度轨迹跟踪.

在考虑外部扰动因素的情况下，本文提出一种 MPC迭代学习的四旋翼无人机轨迹跟踪控制方法. 与现有结果相比，本文提出的基于MPC反馈和ILC前馈结合的新方法能够提升无人机系统的鲁棒性，提高跟踪的准确性，能够很好地抵御外部扰动带来的影响. 与文献 ^[16] 和文献 ^[20] 中的方法相比，实验结果表明本文所提方法轨迹跟踪精度更高，且能够减少迭代次数，降低计算量. 本文主要贡献和创新性如下:

1）设计模型预测控制器作为四旋翼无人机轨迹跟踪的反馈控制器，且在MPC中引入误差补偿进行反馈矫正;

2）设计迭代学习控制器作为四旋翼无人机轨迹跟踪前馈控制器，且使用双曲正切函数优化迭代学习的控制增益，能够减少迭代次数，进而加快收敛速度;

3）首次在MPC框架内引入迭代学习子控制器，将模型预测反馈控制和迭代学习前馈控制相结合，提出一种基于MPC的迭代学习控制新方法，该方法可以应对外部扰动产生的影响且能够提高轨迹跟踪的精度.

2 问题描述

在建立四旋翼无人机模型之前，本文先做如下假设 ^[9] :

1）四旋翼无人机在起飞至降落过程中不会发生任何形变;

2）四旋翼无人机为完全对称系统，机体坐标原点为其质心. 四旋翼无人机的控制输入为

u = [\begin{matrix} u_{1} \\ u_{2} \\ u_{3} \\ u_{4} \end{matrix}] = [\begin{matrix} F_{1} + F_{2} + F_{3} + F_{4} \\ F_{4} - F_{2} \\ F_{3} - F_{1} \\ M_{4} + M_{2} - M_{1} - M_{3} \end{matrix}],

(1)

式中: F_i和M_i（i = 1，2，3，4）表示为4个旋转翼产生的拉力和4个转子产生的阻力矩; 控制输入u₁表示z轴方向上的升力; 控制输入u₂，u₃和u₄分别表示滚转角、俯仰角和偏航角方向上的力矩.

对于四旋翼无人机的模型的建立，在考虑外部扰动的情况下，使用牛顿第二定律得到位置模型，使用欧拉方程通过旋转矩阵（direction cosine matrix，DCM）将机体坐标转换成世界坐标得到姿态模型. 因此，得到四旋翼无人机位置和姿态的数学模型 ^[20]

\{\begin{matrix} \ddot{x} = \frac{(c o s φ s i n θ c o s γ + s i n φ s i n γ) u_{1}}{m} - \frac{d_{x}}{m}, \\ \ddot{y} = \frac{(c o s φ s i n θ s i n γ - s i n φ c o s γ) u_{1}}{m} - \frac{d_{y}}{m}, \\ \ddot{z} = \frac{(c o s φ c o s γ) u_{1}}{m} - g - \frac{d_{z}}{m}, \\ \ddot{φ} = \frac{((I_{y} - I_{z}) \dot{θ} \dot{γ} + u_{2} l)}{I_{x}} - \frac{d_{φ}}{I_{x}}, \\ \ddot{θ} = \frac{((I_{z} - I_{x}) \dot{φ} \dot{γ} + u_{3} l)}{I_{y}} - \frac{d_{θ}}{I_{y}}, \\ \ddot{γ} = \frac{((I_{x} - I_{y}) \dot{θ} \dot{φ} + u_{4})}{I_{z}} - \frac{d_{γ}}{I_{z}}, \end{matrix}

(2)

其中: m为无人机的质量;

\ddot{x}

，

\ddot{y}

，

\ddot{z}

，

\ddot{φ}

，

\ddot{θ}

和

\ddot{γ}

分别表示四旋翼无人机对于机体坐标轴方向的加速度和3个欧拉角滚转角、俯仰角和偏航角的角加速度; I_x，I_y和I_z为四旋翼无人机3个机体坐标轴的转动惯量; g为重力加速度; d_x，d_y，d_z，d_φ，d_θ和d_γ分别为在3个位置和3个欧拉角方向上的扰动分量; l为四旋翼各旋翼的中心到其质心的距离.

定义状态向量和输出向量如下:

\{\begin{array}{l} X = {[\begin{array}{llllllllllll} x & y & z & φ & θ & γ & \dot{x} & \dot{y} & \dot{z} & \dot{φ} & \dot{θ} & \dot{γ} \end{array}]}^{T}, \\ Y = {[\begin{array}{llll} z & φ & θ & γ \end{array}]}^{T} = c X, \end{array}

(3)

其中: c为4 × 12的输出矩阵; 矩阵c对应的元素c_（1，3），c_（2，4），c_（3，5），c_（4，6）等于1，其余元素为0.

控制目标: 设计模型预测控制器作为反馈控制器，且在MPC中引入误差补偿进行反馈矫正; 同时设计迭代学习控制器作为前馈控制器，且使用双曲正切函数优化迭代学习的控制增益. 在外部扰动存在的情况下，通过MPC迭代学习算法实现对四旋翼无人机的高精度轨迹跟踪.

3 控制方案

本文反馈控制器采用MPC算法，以z方向为例，根据四旋翼无人机位置模型式（2）可以得到z方向的子模型，如下:

{\dot{X}}_{z} = {[\begin{matrix} \dot{z} \ddot{z} \end{matrix}]}^{T} = [\begin{matrix} \dot{z} {\frac{(c o s φ c o s γ) u_{1}}{m} - g - \frac{d_{z}}{m}]}^{T} . \end{matrix}

(4)

将z方向子模型离散化成离散标定系统，公式如下:

\begin{matrix} X_{z} (k + 1 ∣ k) = A_{z} X_{z} (k ∣ k) + B_{z} u_{1} (k ∣ k) + \\ D_{z} (k ∣ k), \end{matrix}

(5)

其中: A_z表示与X_z相关的雅可比矩阵; B_z表示与u₁ 相关的雅可比矩阵; D_z为z轴方向的扰动分量. 其中 A_z和B_z的矩阵表示如下:

A_{z} = [\begin{matrix} 1 & Δ t \\ 0 & 1 \end{matrix}]

(6)

B_{z} = [\begin{matrix} 0 \\ \frac{c o s φ c o s γ}{m} Δ t \end{matrix}],

(7)

其中∆t表示为采样时间. 对离散化式（5）进行模型预测p个步长可以得到如下公式:

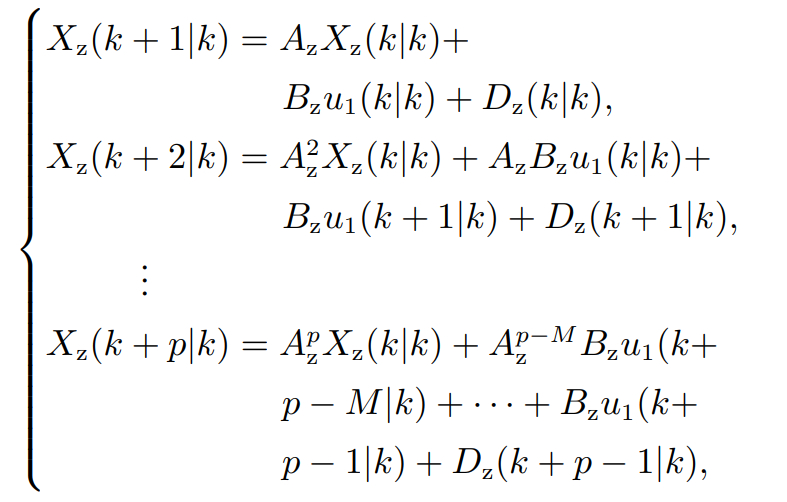
(8)

其中: p为模型预测的预测步长; M为模型预测的控制步长. 将式（8）简化成以下通式:

\begin{matrix} X_{z} (k + i ∣ k) = A_{z}^{i} X_{z} (k + i - 1 ∣ k) + \\ A_{z}^{i - j} B_{z} u_{1} (k + i - j ∣ k) + \dots + \\ B_{z} u_{1} (k + i - 1 ∣ k) + \\ D_{z} (k + i - 1 ∣ k), \end{matrix}

(9)

其中: i =（1，2，· · ·，p），j =（1，2，· · ·，M）.

使用一阶滤波重新计算预测控制输出，目的是去除信号中的高频噪声以达到更好的控制效果，其表示如下:

\begin{matrix} w_{z} (k + i ∣ k) = α {\hat{X}}_{z} (k + i - 1 ∣ k) + \\ (1 - α) X_{z d} (k + i - 1 ∣ k), \end{matrix}

(10)

其中: w_z表示为在z方向上通过一阶滤波重新计算预测控制输出; α表示为滤波器系数，0 <α <1，α决定了当前的预测控制输出X_z值对未来预测控制输出的影响程度，滤波器中的α系数越大对于输入信号就越敏感，而α系数越小会使预测控制输出越平滑; X_zd表示为z方向上期望控制输出.

模型预测算法的目标函数由两部分构成，目标函数1是使预测控制输出趋近与期望轨迹，用期望轨迹与预测控制输出的差方表示，表达如下:

J_{1} = \sum_{i = 1}^{p} {[w_{z} (k + i ∣ k) - X_{z d} (k + i ∣ k)]}^{2},

(11)

目标函数2是四旋翼无人机在轨迹跟踪过程中所需要的能量，表达如下:

J_{2} = \sum_{j = 1}^{M} {[u_{1} (k + j - 1 ∣ k)]}^{2},

(12)

由式（11）–（12）得到模型预测的目标函数

\begin{matrix} J_{z} = J_{1} + J_{2} + ρ δ^{2} = \\ q \sum_{i = 1}^{p} {[X_{z d} (k + i ∣ k) - w_{z} (k + i ∣ k)]}^{2} + \\ r \sum_{j = 1}^{M} {[u_{1} (k + j - 1 ∣ k)]}^{2} + ρ δ^{2}, \end{matrix}

(13)

其中: q与r分别为目标函数1和目标函数2的权重系数; δ为松弛因子; ρ为松弛因子的权重系数. 为目标函数添加松弛因子的目的是为了防止控制器在求解过程中出现无法求解的情况. 将目标函数（13）用矩阵形式表示如下:

\begin{matrix} J_{z} = {(X_{z d} - W_{z})}^{T} Q (X_{z d} - W_{z}) + \\ U_{1}^{T} R U_{1} + ρ δ^{2}, \end{matrix}

(14)

上式中: X_zd为p × 1的z方向期望控制输出矩阵; W_z 为p × 1的一阶滤波计算的z方向预测控制输出矩阵; Q为p × p的目标函数1中权重系数矩阵; U₁为M × 1 的模型预测z方向控制输入矩阵; R为M × M的目标函数2中权重系数矩阵; p和M分别为预测步长和控制步长.

目标函数为二次多项式，将模型预测控制问题转化为如下的二次规划问题:

\begin{matrix} m i n J = \\ m i n (\frac{1}{2} {[\begin{matrix} U_{1} \\ δ \end{matrix}]}^{T} [\begin{matrix} 2 ({(α σ_{z})}^{T} Q (α σ_{z}) + R) & 0 \\ 0 & 2 ρ \end{matrix}] [\begin{matrix} U_{1} \\ δ \end{matrix}] + \\ [\begin{matrix} - 2 E_{z}^{T} Q (α σ_{z}) & 0 \end{matrix}] [\begin{matrix} U_{1} \\ δ \end{matrix}] + E_{z}^{T} Q E_{z}) \end{matrix}

\begin{matrix} s . t . W_{z} (k ∣ k) = X_{z} (k ∣ k), \\ W_{z} (k + i + 1 ∣ k) = \\ α Y_{z} (k + i ∣ k) + (1 - α) X_{z d} (k + i ∣ k), \\ U_{1 m i n} ⩽ U_{1} (k ∣ k) ⩽ U_{1 m a x}, \end{matrix}

(15)

其中E_z = α（X_zd+ ψ_zX_z + D_z）.

姿态方向上控制输入u₂，u₃和u₄的求解的方法与 z方向上的控制输入u₁类似，故可以得到

u^{m p c} = {[\begin{matrix} u_{1} u_{2} u_{3} u_{4} \end{matrix}]}^{T} .

(16)

由于外界干扰对四旋翼无人机控制系统的影响，MPC计算的控制输出的预测值与实际值存在偏差，仅通过上述位置与姿态控制器和滚动优化求解的控制输入，无法保证四旋翼无人机能够准确跟踪期望轨迹，因此需要对位置和姿态控制器继续进行反馈矫正，以 z方向为例，引入预测误差如下:

e_{z} (k + 1 ∣ k) = w_{z} (k + 1 ∣ k) - X_{z d} (k ∣ k) .

(17)

预测误差是对位置与姿态上的MPC控制器预测的预测输出不准确现象的反映，所以使用预测误差来修整预测输出，矫正公式如下:

w_{z 1} (k + 1 ∣ k) = w_{z} (k ∣ k) - K_{z} e_{z} (k ∣ k) .

(18)

为了让无人机在迭代过程中能够快速的收敛，达到预期的跟踪效果，使用双曲正切函数来优化迭代学习增益，降低迭代次数，公示如下:

\begin{matrix} u_{k + 1}^{I L C} = u_{k} + k_{p} t a n h (Δ e_{k}) e_{k} + \\ k_{d} t a n h (Δ {\dot{e}}_{k}) {\dot{e}}_{k}, \end{matrix}

(19)

式中:

u_{k + 1}^{I L C}

为自适应迭代学习控制第 k + 1 次输出; tanh x为双曲正切函数; ∆e_k和∆

{\dot{e}}_{k}

分别为上次迭代跟踪误差和本次迭代跟踪误差的变化值、上次迭代跟踪微分误差和本次迭代跟踪微分误差的变化值，具体公式如下:

t a n h x = μ \frac{e^{x} - e^{- x}}{e^{x} + e^{- x}} .

(20)

由于tanh x的值域为[−µ，µ]，从而可以改变控制增益的倍数，加快四旋翼无人机轨迹跟踪的收敛速度.

综合上述公式，设计的MPC迭代学习控制器如下:

\{\begin{matrix} u_{k + 1}^{I L C} = u_{k} + k_{p} t a n h (Δ e_{k}) e_{k} + \\ k_{d} t a n h (Δ {\dot{e}}_{k}) {\dot{e}}_{k}, \\ u_{k} = u^{m p c} + u_{k}^{I L C}, \end{matrix}

(21)

式中u_k为MPC迭代学习控制器第k次的控制输入.

4 基于MPC迭代学习系统稳定性分析

定理 1 当四旋翼无人机初始状态位于 X_k（0）时，对其施加控制u_k（t），如果四旋翼无人机控制系统满足以下条件:

1）

‖ (I - (W_{k} c_{1} + L_{k} c_{2}) B_{k} ‖ ⩽ ρ ⩽ 1 ，

其中: ρ为谱半径，I为单位矩阵，c₁和c₂为MPC迭代学习算法中迭代学习增益矩阵，W_k= tanh（∆e_k）和L_k= tanh（∆

{\dot{e}}_{k}

）为算法中自适应迭代学习增益矩阵;

2）外部扰动D_k有界，即

\underset{t \in [0 ， T]}{s u p} ‖D_{k}‖ ⩽ b_{D}

；

3）

X_{k} （ 0 ） = X_{0} ， Y_{k} （ t ） = Y_{d} （ t ）

，则当k → ∞时，那么预测的控制输出趋近于期望输出.

证在第k + 1次的迭代学习控制误差为

\begin{matrix} Δ u_{k + 1}^{I L C} (t) = u_{d} (t) u_{k + 1} (t) = \\ u_{d} (t) - (u_{k} + W_{k} c_{1} e_{k} + L_{k} c_{2} {\dot{e}}_{k}), \end{matrix}

(22)

式中:

Δ u_{k + 1}^{I L C} （ t ）

为第k + 1次迭代控制输入与期望控制输入的差值; u_d（t）为四旋翼无人机系统的期望控制输入.

四旋翼无人机控制系统的输出误差表示为

e_{k} (t) = Y_{d} (t) - Y_{k} (t) = c [X_{d} (t) - X_{k} (t)]

(23)

设四旋翼无人机控制系统的微分方程为

{\dot{X}}_{k} (t) = A X_{k} (t) + B u_{k} (t) + D_{k} .

(24)

对上式微分方程求解可以得到

X_{k} (t) = X_{0} e^{A t} + \int_{0}^{τ} e^{A (t - τ)} u_{k} (τ) d τ + D_{k} e^{A t}

(25)

将上式带入到四旋翼无人机控制系统的输出误差式（23）中可得

e_{k} (t) = \int_{0}^{t} (c + D_{k}) e^{A (t - τ)} B Δ u_{k} (τ) d τ

(26)

对上式两边求导可得

\begin{matrix} {\dot{e}}_{k} (t) = (c + D_{k}) B Δ u_{k} (t) + \\ \int_{0}^{t} (c + D_{k}) A e^{A (t - τ)} B Δ u_{k} (τ) d τ . \end{matrix}

(27)

将式（25）–（26）代入式（21）可得

\begin{matrix} Δ u_{k + 1} (t) = (I - B L_{k} c_{2} (c + D_{k})) Δ u_{k} (t) - \\ \int_{0}^{t} (c + D_{k}) (A W_{k} c_{1} + \\ L_{k} c_{2}) e^{A (t - τ)} B Δ u_{k} (τ) d τ . \end{matrix}

(28)

对式（28）两端同乘e⁻^λt，同时利用λ范数定义 ^[20]

\begin{matrix} e^{- λ t} ‖Δ u_{k + 1} (t)‖ ⩽ \\ ‖I - B L_{k} c_{2} (c + D_{k}) e^{- λ t}‖ Δ u_{k} (t) ‖ - \\ b \int_{0}^{t} e^{- λ (t - τ)} e^{- λ t} ‖Δ u_{k} (τ)‖ d τ \end{matrix}

(29)

式中

b = \underset{t \in [0 ， T]}{s u p} ‖(c + D_{k}) (A W_{k} c_{1} + L_{k} c_{2}) B‖

，由范数定义可知

{‖Δ u_{k + 1} (t)‖}_{λ} ⩽ ρ {‖Δ u_{k} (t)‖}_{λ},

(30)

式中

ρ = ‖I - B L_{k} c_{2} (c + D_{k})‖ + b \frac{1 - e^{- λ t}}{λ} ，

选取足够大的λ ^[20]，ρ的取值可以小于1，此时

\underset{k \to + \infty}{l i m} {‖Δ u_{k + 1} (t)‖}_{λ} = 0

(31)

进一步可以得到

\underset{k \to + \infty}{l i m} {‖e_{k} (t)‖}_{λ} = 0 .

(32)

因此，可证设计的MPC迭代学习控制算法收敛. 证毕.

5 仿真实验及分析

为了检验本文设计的 MPC 迭代学习算法的有效性，在未知扰动的情况下通过MATLAB仿真验证四旋翼无人机飞行轨迹跟踪的准确性和鲁棒性. 此外，还将本文所提方法和现有文献中的方法进行实验对比.

对于式（2）中四旋翼无人机系统的各项参数为: 重力加速度为9.8 m/s²; 机体质量为0.8 kg; 四旋翼机臂长度为 0.12 m; x轴的转动惯量为0.042 12; y轴的转动惯量为0.042 12; z轴的转动惯量为0.082 55，迭代算法中的k_p为0.1，k_d为10，tanh x中µ的值为1.

本文采用连续的位置、速度和加速度作为参考轨迹，使得四旋翼无人机的跟踪轨迹更加平滑

\{\begin{matrix} x_{d} (t) = \frac{6 s i n \frac{π}{5 t} c o s \frac{π}{5 t}}{1 + s i n {(\frac{π}{5 t})}^{2}} \\ y_{d} (t) = \frac{4 c o s \frac{π}{5 t}}{1 + s i n {(\frac{π}{5 t})}^{2}} \\ z_{d} (t) = s i n \frac{π}{5 t} \end{matrix}

(33)

为了模拟外界风对四旋翼无人机产生的干扰影响，本文选取如下的扰动 ^[20]:

\{\begin{matrix} D = 10 + 20 s i n (2 π t) \\ D_{z} = 0.1 D, D_{φ} = 0.15 D \\ D_{θ} = 0.5 D, D_{γ} = 0.001 D \end{matrix}

(34)

其中: D_z为轴的扰动分量; D_φ为滚转角扰动分量; D_θ 为俯仰角扰动分量; D_γ为偏航角扰动分量.

四旋翼无人机作为一个欠驱动系统，需要通过控制姿态角来控制x和y位置，将期望偏航角设为0^◦，得到期望滚动角和俯仰角 ^[20]

\{\begin{matrix} φ_{d} = - \frac{1}{g} ({\ddot{x}}_{d} s i n γ_{d} - {\ddot{y}}_{d} c o s γ_{d}), \\ θ_{d} = - \frac{1}{g} ({\ddot{x}}_{d} c o s γ_{d} + {\ddot{y}}_{d} s i n γ_{d}) . \end{matrix}

(35)

图1为无人机三维运动轨迹，给出了期望、未迭代和第5次迭代后的3D轨迹跟踪对比图. 黑色曲线表示期望轨迹，红色曲线表示单一 MPC（未迭代）控制下的轨迹，绿色曲线表示的是本文提出的在第5次迭代后 MPC迭代学习控制下的轨迹. 由图1可见，本文所设计的方法和单一的MPC方法都能实现轨迹跟踪，但本文提出的方法在跟踪精度上显然优于单纯的MPC方法，MPC方法轨迹大体能跟上，但误差特别大. 因此，在外部扰动存在的情况下，本文所设计的基于MPC迭代学习控制方法具有较强的鲁棒性，跟踪精度高.

图1期望、未迭代和第5次迭代后的3D轴轨迹

Fig.1Expected, non-iterated and the5th iterations 3D trajectories

图2给出了z轴方向上的的期望、未迭代和第3与5 次迭代后的轨迹对比图. 由图2可知，第5次迭代后的 MPC迭代学习控制下轨迹基本完全重合与期望轨迹，表明其跟踪精度最高.

图

3–5分别给出了四旋翼无人机在滚转角、俯仰角和偏航角方向上的期望、未迭代和第3与第5次迭代后的轨迹对比图. 由图可得，本文提出的5次迭代后的MPC迭代学习控制方法具有强鲁棒性，跟踪精度最高.

为了进一步验证本文所设计的方法具有强鲁棒性且跟踪精度高，与文献 ^[16] 中的滑模迭代控制和文献 ^[20]中的鲁棒迭代控制方法进行实验对比. 图6给出了MPC迭代、滑模迭代与鲁棒迭代跟踪误差对比图.

根据图6可以看出，相比于文献 ^[16] 中滑模迭代方法和文献 ^[20] 中鲁棒迭代算法的初始迭代跟踪误差，本文提出的MPC迭代算法在初始迭代误差最小，约为4.7，而前两种方法误差分别为7.8和12.

图2期望、未迭代和第3与5次迭代后的z轴轨迹

Fig.2Expected, non-iterated and the5th iterated z axis trajectories

图3期望、未迭代和第3与5次迭代的滚转角轨迹

Fig.3Expected, non-iterated and the3rd and 5th iterated roll angle trajectories

图4期望、未迭代和第3与5次迭代的俯仰角轨迹

Fig.4Expected, non-iterated and the3rd and 5th iterated pitch angle trajectories

此外，在图6中，经过第5次迭代后，MPC迭代学习算法的跟踪误差已经接近于零，而相比之下，其他两个算法的误差则在第7次迭代后才逐渐趋近于零. 这表明，相比于现有文献 ^[16，20] 中的方法，MPC迭代学习算法在四旋翼无人机轨迹跟踪控制系统中具有更快的收敛速度，能够在较少的迭代次数内降低跟踪误差.

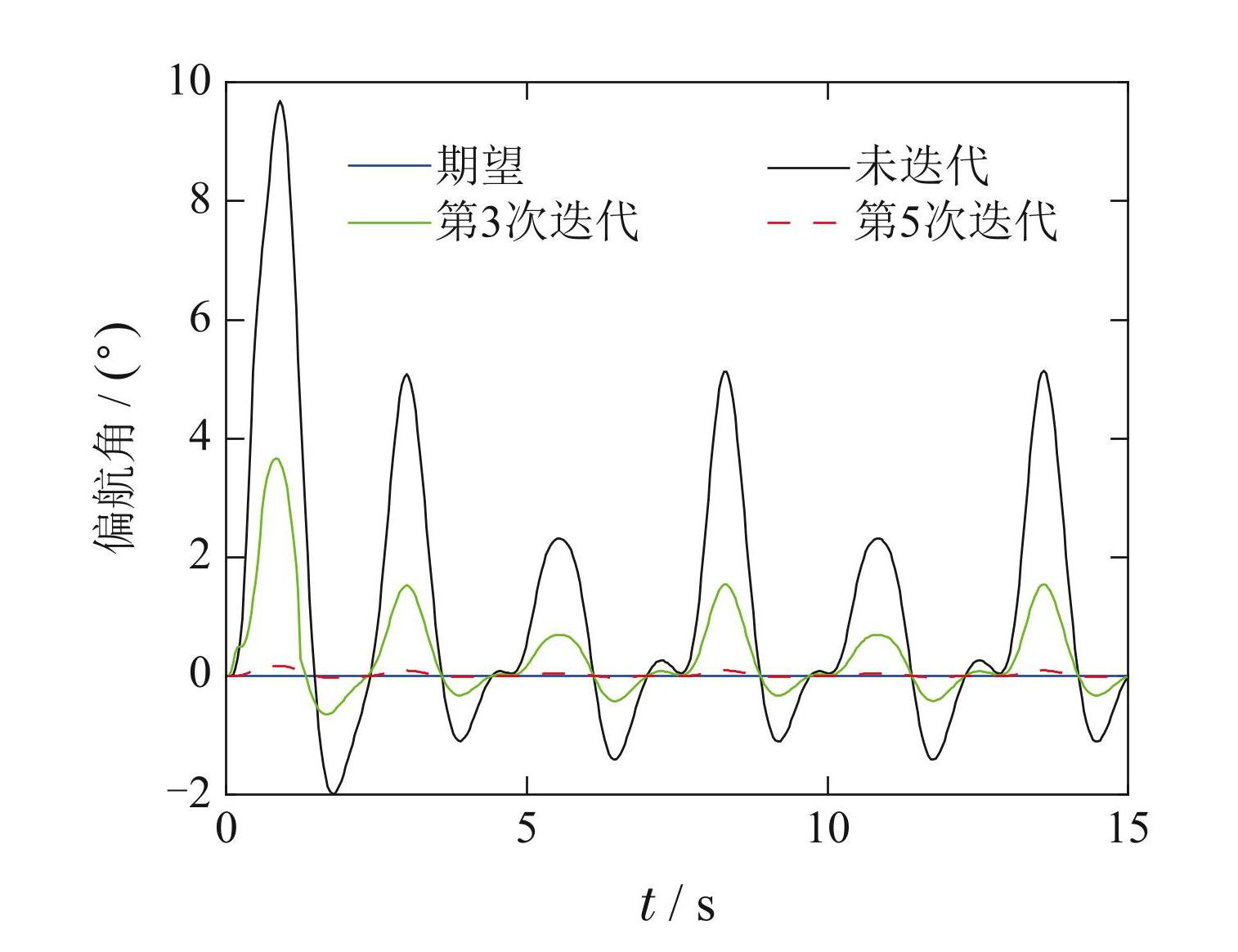
图5期望、未迭代和第3与5次迭代的偏航角轨迹

Fig.5Expected, non-iterated and the3rd and 5th iterated yaw angle trajectories

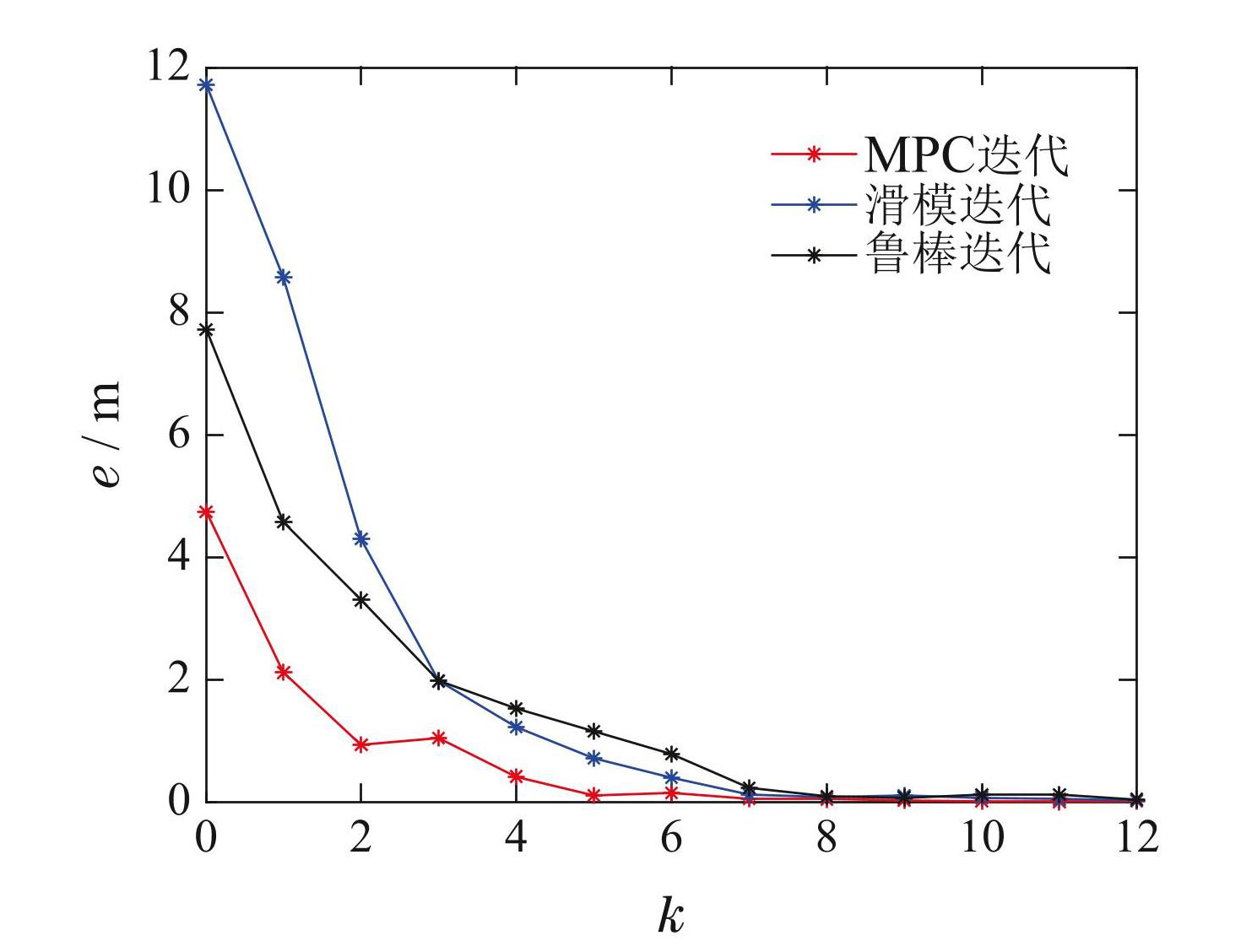
图6MPC迭代、滑模迭代与鲁棒迭代误差对比图

Fig.6Comparison chart of MPC iteration, sliding mode iteration and robust iteration error

6 结束语

本文针对存在外部扰动情况下的四旋翼无人机系统，设计了MPC迭代学习控制算法. MPC子控制器作为反馈控制器，迭代学习子控制器作为前馈控制器，使用双曲正切函数来自适应调整迭代学习参数可以减少迭代次数，降低计算量，同时提高跟踪精度. 未来将搭建无人机实验平台进行实验验证，并研究网络攻击环境下无人机系统的模型预测安全控制问题.

图1期望、未迭代和第5次迭代后的3D轴轨迹

Fig.1Expected, non-iterated and the5th iterations 3D trajectories

下载: 全尺寸图片

图2期望、未迭代和第3与5次迭代后的z轴轨迹

Fig.2Expected, non-iterated and the5th iterated z axis trajectories

下载: 全尺寸图片

图3期望、未迭代和第3与5次迭代的滚转角轨迹

Fig.3Expected, non-iterated and the3rd and 5th iterated roll angle trajectories

下载: 全尺寸图片

图4期望、未迭代和第3与5次迭代的俯仰角轨迹

Fig.4Expected, non-iterated and the3rd and 5th iterated pitch angle trajectories

下载: 全尺寸图片

图5期望、未迭代和第3与5次迭代的偏航角轨迹

Fig.5Expected, non-iterated and the3rd and 5th iterated yaw angle trajectories

下载: 全尺寸图片

图6MPC迭代、滑模迭代与鲁棒迭代误差对比图

Fig.6Comparison chart of MPC iteration, sliding mode iteration and robust iteration error

下载: 全尺寸图片

图1期望、未迭代和第5次迭代后的3D轴轨迹

Fig.1Expected, non-iterated and the5th iterations 3D trajectories

图2期望、未迭代和第3与5次迭代后的z轴轨迹

Fig.2Expected, non-iterated and the5th iterated z axis trajectories

图3期望、未迭代和第3与5次迭代的滚转角轨迹

Fig.3Expected, non-iterated and the3rd and 5th iterated roll angle trajectories

图4期望、未迭代和第3与5次迭代的俯仰角轨迹

Fig.4Expected, non-iterated and the3rd and 5th iterated pitch angle trajectories

图5期望、未迭代和第3与5次迭代的偏航角轨迹

Fig.5Expected, non-iterated and the3rd and 5th iterated yaw angle trajectories

图6MPC迭代、滑模迭代与鲁棒迭代误差对比图

Fig.6Comparison chart of MPC iteration, sliding mode iteration and robust iteration error

图1期望、未迭代和第5次迭代后的3D轴轨迹

Fig.1Expected, non-iterated and the5th iterations 3D trajectories

图2期望、未迭代和第3与5次迭代后的z轴轨迹

Fig.2Expected, non-iterated and the5th iterated z axis trajectories

图3期望、未迭代和第3与5次迭代的滚转角轨迹

Fig.3Expected, non-iterated and the3rd and 5th iterated roll angle trajectories

图4期望、未迭代和第3与5次迭代的俯仰角轨迹

Fig.4Expected, non-iterated and the3rd and 5th iterated pitch angle trajectories

图5期望、未迭代和第3与5次迭代的偏航角轨迹

Fig.5Expected, non-iterated and the3rd and 5th iterated yaw angle trajectories

图6MPC迭代、滑模迭代与鲁棒迭代误差对比图

Fig.6Comparison chart of MPC iteration, sliding mode iteration and robust iteration error

YAO Qianqian, QI Guoyuan. Model compensation optimal control of quadrotor unmanned aerial vehicle systems. Control Theory & Applications,2024,23(5):1-9.(姚倩倩, 齐国元. 四旋翼无人机系统模型补偿最优控制. 控制理论与应用,2024,23(5):1-9.)

SUN Miaoping, LIU Jingjing, NIAN Xiaohong,et al. Robust tracking control of quadcopter unmanned aerial vehicles based on interval matrices. Control Theory & Applications,2017,34(2):168-178.(孙妙平, 刘静静, 年晓红, 等. 基于区间矩阵的四旋翼无人机鲁棒跟踪控制. 控制理论与应用,2017,34(2):168-178.)

LOPEZ-SANCHEZ I, MORENO-VALENZUELA J. PID control of quadrotor UAVs: A survey. Annual Reviews in Control,2023, DOI:10.1016/j.arcontrol.2023.100900.

ZHANG X, XIAN B, ZHAO B,et al, Autonomous flight control of a nano quadrotor helicopter in a GPS-denied environment using onboard vision. IEEE Transactions on Industrial Electronics,2015,62(10):6392-6403.

ALEXIS K, NIKLAKOPOULOS G, TZES A. On trajectory tracking model predictive control of an unmanned quadrotor helicopter subject to aerodynamic disturbances. Asian Journal of Control,2014,16(1):209-224.

WANG Z, ZHAO T. Based on robust sliding mode and linear active disturbance rejection control for attitude of quadrotor load UAV. Nonlinear Dynamics,2022,108(4):3485-3503.

BAEK J, KANG J. A Synthesized sliding-mode control for attitude trajectory tracking of quadrotor UAV systems. IEEE-ASME Transactions on Mechatronics,2023,28(4):2189-2199.

WANG Shubo, HAN Yu, CHEN Jian,et al. Active disturbance rejection control of UAV attitude based on iterative learning control. Acta Aeronauticaet Astronautica Sinica,2020,41(12):319-331.(王术波, 韩宇, 陈建, 等. 基于ADRC迭代学习控制的四旋翼无人机姿态控制. 航空学报,2020,41(12):319-331.)

ZHANG M, SHAOHUA W, JIAO J,et al. Energy-and cost-efficient transmission strategy for UAV trajectory tracking control: A deep reinforcement learning approach. IEEE Internet of Things Journal,2023,10(10):8958-8970.

WANG Xiaohai, MENG Xiuyun, LI Chuanxu. Design of UAV trajectory tracking controller based on MPC. Systems Engineering and Electronic Technology,2021,43(1):191-198.(王晓海, 孟秀云, 李传旭. 基于MPC的无人机航迹跟踪控制器设计. 系统工程与电子技术,2021,43(1):191-198.)

MANZOOR T, XIA Y, ZHAI D H,et al. Trajectory tracking control of a VTOL unmanned aerial vehicle using offset-free tracking MPC. Chinese Journal of Aeronautics,2020,33(7):2024-2042.

RODRIGUEZ-PIEIRO J, HUANG Z, CAI X,et al. Geometry-based MPC tracking and modeling algorithm for time-varying UAV channels. IEEE Transactions on Wireless Communications,2021,20(4):2700-2715.

CAO Yuqi, FU Haoran, GAO Fei,et al. A trajectory tracking control algorithm for a canard wing tail seat vertical takeoff and landing unmanned aerial vehicle based on MPCC. Journal of Aeronautics,2023,44(S2):501-511.(曹煜琪, 付皓然, 高飞, 等. 基于MPCC的鸭翼尾座式垂直起降无人机轨迹跟踪控制算法. 航空学报,2023,44(S2):501-511.)

YE Dapeng, CHEN Shuda, ZHANG Zhide. Four rotor trajectory tracking control based on online Gaussian model driven MPC. Flight Mechanics,2025,43(1):56-62.(叶大鹏, 陈书达, 张之得. 基于在线高斯模型驱动MPC的四旋翼轨迹跟踪控制. 飞行力学,2025,43(1):56-62.)

YAN D, ZHANG W, CHEN H,et al. Robust control strategy for multi-UAVs system using MPC combined with Kalman-consensus filter and disturbance observer. ISA Transactions,2023,135:35-51.

WANG Juan, ZHAO Chengjing, DONG Shenghao. Trajectory tracking of four rotor unmanned aerial vehicle based on sliding mode adaptive iterative learning. Electronics Optics Control,2024,31(3):36-40.(王娟, 赵成璟, 董升昊. 基于滑模自适应迭代学习的四旋翼无人机轨迹跟踪. 电光与控制,2024,31(3):36-40.)

WANG S B, HAN Y, CHEN J,et al. Active disturbance rejection control of UAV attitude based on iterative learning control. Acta Aeronautica et Astronautica Sinica,2020,41(12):319-331.

MERAGLIA S, LOVERA M. Smoother-based iterative learning control for UAV trajectory tracking. IEEE Control Systems Letters,2022,6:1501-1506.

XINGJIAN F, PENG J. Iterative learning control for UAVs formation based on point-to-point trajectory update tracking. Mathematics and Computers in Simulation,2023,209:1-15.

CHEN Tieyi, ZHU Chengzhi, WEI Wenli,et al. Trajectory tracking of quadcopter unmanned aerial vehicles based on robust iterative learning. Flight Mechanics,2022,40(2):46-52,60.(陈铁义, 朱承治, 魏文力, 等. 基于鲁棒迭代学习的四旋翼无人机轨迹跟踪. 飞行力学,2022,40(2):46-52,60.)