欢迎访问《控制理论与应用》期刊网站！

数据驱动下的多指混杂机械臂控制与抓取

doi: 10.7641/CTA.2025.40325

孙浪浪¹ ，何邵颖¹ ，徐云雯¹ ，陈友仁¹ ，潘旭华²

1. 上海交通大学电子信息与电气工程学院, 上海 200240

2. 浙江大学滨江研究院, 浙江杭州 310051

基金项目: 国家自然科学基金项目(61973214, 62261160385, 62103271)资助.

详细信息

作者简介

孙浪浪硕士研究生,目前研究方向为柔性夹爪控制、机械臂抓取等,E-mail: sunlanglang@sjtu.edu.cn;

何邵颖从事博士后研究工作,目前研究方向为柔性夹爪设计及控制、视觉伺服等,E-mail: heshaoying19941204@sjtu.edu.cn;

徐云雯副教授,硕士生导师,目前研究方向为预测控制应用、智能交通系统等,E-mail: willing419@sjtu.edu.cn;

陈友仁高级工程师,目前研究方向为智能交通系统、信息融合等,E-mail: yrchen@sjtu.edu.cn;

潘旭华硕士研究生,目前研究方向为工业软件、智能工厂等,E-mail: panxuhua@zju-bj.com.

通信作者

何邵颖，E-mail: heshaoying19941204@sjtu.edu.cn;Tel.:+8613262992069.

Data-driven control and grasping of multi-finger hybrid robotic arm

SUN Lang-lang¹ ， HE Shao-ying¹ ， XU Yun-wen¹ ， CHEN You-ren¹ ， PAN Xu-hua²

1. School of Electronic Information and Electrical Engineering, Shanghai Jiao Tong University, Shanghai 200240 , China

2. Binjiang Institute of Zhejiang University, Hangzhou Zhejiang 310051 , China

Funds: Supported by the National Natural Science Foundation of China (61973214, 62261160385, 62103271).

摘要

本文设计了多指混杂机械臂控制系统及其抓取控制方法, 对于抓取任务, 刚柔混杂的设计结构同时提高了控制的精确性以及与物体交互的安全性. 本文分别采用旋量理论和分段常曲率方法对机械臂的刚体和柔性部分进行运动学建模, 最终得到基于雅克比矩阵的刚柔混杂机械臂一体化模型. 此外, 为削弱模型偏差对系统控制性能的影响, 本文提出了基于输入映射的数据驱动和模型预测控制相结合的方法, 用历史数据替换部分不精确的系统模型, 同时利用历史数据的线性组合来构造当前时刻的状态和控制输入, 以完成对柔性夹爪位姿的控制, 柔性夹爪末端的轨迹跟踪仿真反映该控制器的性能良好. 在此基础上, 本文设计了基于被抓物体姿态的精确抓取与包络抓取方法, 并通过ArUco方块抓取实验证实了该方法的有效性.

关键词

混杂机械臂 / 模型预测控制 / 输入映射 / 数据驱动 / 抓取控制

Abstract

In this paper, a multi-finger hybrid robotic arm control system and its grasping control method are designed. The rigid-flexible hybrid structure enhances both the accuracy of control and the safety of object interaction during grasping tasks. Kinematic modeling of the rigid and flexible components of the robotic arm is performed using screw theory and the piecewise constant curvature method, respectively. An integrated model of the rigid-flexible hybrid robotic arm, based on the Jacobian matrix, is then derived. To mitigate the impact of model inaccuracies on system performance, a novel approach is proposed that combines data-driven techniques with model predictive control. This method replaces portions of the imprecise system model with historical data and constructs the current state and control inputs through a linear combination of this data. The effectiveness of this approach in controlling the posture of the flexible gripper is demonstrated through favorable trajectory tracking results in simulations. Building upon this, an accurate grasping and enveloping grasping method based on the posture of the grasped object is developed, and the validity of the method is confirmed through ArUco cube grasping experiments.

Keywords

hybrid robotic arm / model predictive control / input mapping / data-driven / grasping control

1 引言 2 多指刚柔混杂机械臂平台设计 2.1 混杂机械臂结构设计 2.2 实验平台搭建 3 多指刚柔混杂机械臂建模 4 基于输入映射的柔性夹爪位姿控制 4.1 机械臂模型输入映射描述 4.2 基于输入映射和MPC的控制器设计 4.3 基于物体姿态的柔性夹爪抓取算法 5 多指柔性夹爪的控制及抓取实验 5.1 输入映射位姿控制仿真验证 5.2 实物抓取实验 6 结论

1 引言

在自动化和机器人领域，机械臂抓取已经成为研究的关键领域之一 ^[1-3] . 由于刚性机械臂具有的高精度和高负载能力，它们通常是抓取机械臂的首选. 文献 ^[4] 将双臂操作与模型预测控制（model predictive control，MPC）相结合，通过调整协作指数，将协作抓取任务分为跟踪、动作同步、阻抗和力优先等方式.文献 ^[5] 中提出了用于对象的搜索、接近和抓取（searching，approaching and grasping，SAG）的控制流程，在物体抓取运输研究领域提供了一种新的思路. 针对现有抓取技术在复杂环境下难以进行有效的目标导向性抓取的问题，文献 ^[6] 提出了一种基于深度强化学习的推动和目标物抓取方法.

然而，在许多应用场景中，确保人机交互的安全性以及对柔软物体的精细操控至关重要. 例如，在食品加工厂进行分拣或为患者设计医疗辅助设备. 在这些场景下，相比于刚性夹爪，柔性夹爪在环境适应性、安全性方面具备显著优势，能够在操作中实现对不规则或易损物体的无损抓取，应用场景广泛.2020年麻省理工学院研制了一种使用硅树脂制作而成的柔性夹爪 ^[7]，该夹爪不仅能够抓取不同种类的物体，还能感知识别该物体的种类. 文献 ^[8] 设计的柔性夹爪可变换自身构型，通过调整工作空间以适用不同物体的抓取. 文献 ^[9] 将柔性机构装在universal robots（UR）刚体机械臂末端，以完成疫情期间的核酸采样工作.

与传统的使用刚性夹爪或柔性夹爪抓取相比，刚体机械臂与柔性夹爪结合的混合设计结构更有优势，能同时利用刚体机械臂定位精度高以及柔性夹爪与环境交互具有安全性的优势. 柔性夹爪对脆弱物体的抓取有着天然的优势 ^[10]，但由于需要考虑材料的弯曲、拉伸等特性，使其建模更加复杂 ^[11] . 柔性夹爪的建模方法主要包括分段常曲率法（piecewise constant curvature，PCC）^[12]、Cosserat理论 ^[13] 和有限元法（finite element method，FEM）^[14] . Cosserat建模依赖于材料属性的精确测量，但这些属性在实际中很难准确测定 ^[15] . 利用FEM进行建模会带来计算负担，影响控制的实时性 ^[16] . PCC方法由于其简洁性被广泛应用于柔性夹爪的建模，该方法将柔性夹爪分为有限段恒定曲率的部分，每一段可以使用曲率、长度、偏心角等参数来描述空间曲线的位姿，从而可以用Denavit-Hartenberg参数法 ^[17] 或者旋量理论 ^[18] 求解柔性夹爪的齐次变换矩阵.

为了使得柔性夹爪能够实现较强的伸缩、弯曲和扭转等形变，故而不能使用刚性机械臂的连杆驱动方式. 文献 ^[19] 将目前主流驱动柔性夹爪的方式分为3大类: 拉线驱动、形状记忆合金驱动和气动驱动 ^[20-22] . 文献 ^[23] 将气动三指柔性夹爪被安装在 UR机械臂的末端，利用sofa对柔性夹爪进行动力学建模，最终实现抓取. 然而，对气动臂进行动力学分析是一个复杂的过程，并且气动装置不适用于小型抓取机构的设计. 针对封闭空间内的轨道维护操作，文献 ^[24] 提出了一种基于受限空间操作性优化的刚柔混合双臂协调的轨迹规划方法，该柔性夹爪采用线驱方式，由电机带动拉线直接操作，因此反映迅速，但由于拉线需要在狭小空间内穿梭，会导致传动效率的损失. 对于混杂机械臂抓取任务而言，柔性夹爪的控制是主要难点. 由于模型不精确和低精度的驱动机构，控制器的计算将受到影响，并且控制器的指令可能无法被驱动器精确执行 ^[25] . 因此，建模的不精确性和实际混合机器人的复杂性给控制器的设计带来极大问题 ^[26] . 文献 ^[22] 设计了丝驱柔性夹爪，采用自适应控制方法，考虑材料的粘性与应变、轨迹精度良好，但未考虑系统摩擦，且系统建模复杂. 文献 ^[27] 通过补偿线缆耦合并采用动态控制，但精度有限. 文献 ^[28] 提出一种端到端的两阶段神经网络柔性控制思想和异步Transformer执行策略，但神经网络的训练较为繁琐. 文献 ^[29] 采用深度学习控制，无需对柔性夹爪进行建模，且不需要视觉反馈，但是算法控制的范围有限.

针对上述问题，本文设计了一个多指混杂机械臂抓取平台，其中柔性夹爪采用拉线驱动的方式，适用于小型柔性夹爪的驱动，该平台的刚柔混杂设计结构旨在提高控制精度和与物体交互的安全性. 为简化建模，分别采用旋量理论和分段常曲率方法对机械臂的刚体和柔性部分进行建模，最终得到了基于雅克比矩阵的混杂机械臂一体化模型. 由于建模过程的简化，所建模型与实际模型存在偏差，为削弱模型偏差对系统控制性能的影响，提出输入映射（input-mapping）的数据驱动方法，采用滑动窗格收集历史输入输出数据，然后利用历史数据替换部分不精确模型，从而减少了建模不精确的影响. 此外，本文设计了基于输入映射的模型预测控制器，采用数据驱动方法，利用历史数据的线性组合来构造当前时刻的状态和控制输入. 在所设计的控制器的基础上提出了基于被抓物体姿态的抓取方法，将抓取分为包络抓取和精确抓取，最后分别通过轨迹跟踪仿真和实物抓取实验验证了控制器和抓取方法的有效性.

2 多指刚柔混杂机械臂平台设计

本节主要对多指刚柔混杂机械臂实验平台进行设计，包括多指柔性夹爪的结构设计以及实验平台的搭建.

2.1 混杂机械臂结构设计

如图1所示，本文设计的三指柔性夹爪由热塑性聚氨酯材料制成，该材料具备良好的柔性和弹性，可以承受反复压缩和拉伸而不易损坏，且能适应不同形状和尺寸的物体的抓取. 三指夹爪成120^◦，等距离安装在驱动基座上. 由前文分析可知，气压驱动在小型柔性夹爪中设计困难，且控制更加复杂; 拉线驱动使用电机控制拉线的位移，以此实现精准的位置控制，且更适合于小型结构设计，因此本文选择拉线驱动的方式. 如图1所示，每根柔性夹爪有4个成90^◦十字分布的通孔，4根驱绳分别穿过每根柔性夹爪的通孔，拉线一端固定在柔性夹爪的顶部，一端缠绕在拉线连接装置上，该连接装置由螺钉固定在驱动电机上，将电机转动的角度转换为拉线相应的伸缩量，从而控制柔性夹爪运动. 此外，呈对角分布的两条拉线安装在同一个电机上，因此，该柔性夹爪总共需要6个电机来控制其运动.

六轴刚性机械臂和柔性夹爪通过驱动基座进行连接，驱动基座用于电机、拉线以及拉线连接装置的安装，其底部与刚性机械臂末端通过螺钉固定，顶部安装三指柔性夹爪. 多指刚柔混杂机械臂的总体结构如图2中的刚柔混杂机械臂所示.

图1柔性夹爪结构设计

Fig.1The structure design of the soft robot

图2刚柔混杂机械臂抓取平台

Fig.2The grasping platform of rigid-soft robot

2.2 实验平台搭建

如图2所示，本文实验平台包括多指刚柔混杂机械臂、6个驱动电机、电机控制器、电机供电电源、驱动基座、刚体机械臂电源、控制板、相机以及计算机. 计算机通过串口与刚体机械臂控制板和电机进行通信，分别控制刚体和柔性夹爪的运动. 为方便定位，在被抓物体表面覆盖ArUco码. 相机采用眼在手外安装，通过手眼标定将检测到的被抓物体的位姿信息转换到机械臂基坐标系.

3 多指刚柔混杂机械臂建模

多指混合机械臂的模型是控制算法的基础，本节对六轴刚体机械臂和柔性夹爪进行建模.

六轴刚体机械臂的正运动学模型使用旋量理论建立，其表示为方程（1），即

T_{e} = e^{[S_{1}] θ_{1}} e^{[S_{2}] θ_{2}} e^{[S_{3}] θ_{3}} e^{[S_{4}] θ_{4}} e^{[S_{5}] θ_{5}} e^{[S_{6}] θ_{6}} M

(1)

其中: S_i表示运动旋量; θ_i表示六轴刚体机械臂的关节角; M表示机械臂在初始位置下（即θ_i均为零）末端坐标系相对于基坐标系的齐次变换矩阵.

柔性夹爪与传统的刚体机械臂不同，其夹爪末端的位置和姿态由4根拉线的长度决定. 因此，柔性夹爪的正运动学是解决拉线长度到夹爪末端位姿之间映射关系的问题. 同理，柔性夹爪的微分运动学反映的是拉线速度与夹爪末端速度的关系. 参考文献 ^[30] 的分段常曲率建模方法，得到第i根柔性夹爪末端相对于刚性机械臂基坐标系的齐次变换矩阵为

T_{i} = T_{e} T_{e}^{i} T_{s}^{i}, i = 1,2, 3

(2)

其中:

T_{e}^{i}

表示刚体机械臂末端到驱动基座的齐次变换矩阵，由驱动基座的结构设计以及安装方式决定;

T_{s}^{i}

为驱动基座到柔性夹爪末端的齐次变换矩阵.

将T_i中的姿态部分由旋转矩阵转换为欧拉角表示，ϕ_i = [ψ_i ϑ_i φ_i ]^T，其中ψ_i，ϑ_i，φ_i分别表示夹爪末端绕刚体机械臂基坐标系固定轴x， y， z旋转的角度. 将位置向量表示为p_i = [x_i y_i z_i ]^T，则正运动学公式（2）可改写为

s_{i} = [\begin{matrix} p_{i} \\ ϕ_{i} \end{matrix}] = f (T_{i}) = k (q_{i}),

(3)

其中: q_i = [θ₁ θ₂ · · · θ₆

{θ_{7}^{i} θ_{8}^{i}]}^{T} \in R^{8 \times 1}

，θ₁到θ₆为六轴刚体机械臂的关节角，

θ_{7}^{i}

，

θ_{8}^{i}

为第i根柔性夹爪的拉线长度; f表示齐次变换矩阵到平移和旋转向量的映射; k表示关节空间到操作空间的映射.

将式（3）两边对关节q_i求导，得到混杂机械臂的微分运动学，即

{\dot{s}}_{i} = [\begin{matrix} {\dot{p}}_{i} \\ {\dot{ϕ}}_{i} \end{matrix}] = [\begin{matrix} \frac{\partial p_{i}}{\partial q_{i}} \\ \frac{\partial ϕ_{i}}{\partial q_{i}} \end{matrix}], {\dot{q}}_{i} = J_{A}^{i} (q_{i}) {\dot{q}}_{i},

(4)

其中

J_{A}^{i} (q_{i}) \in R^{6 \times 8}

表示第i根柔性管的解析雅克比矩阵. 为得到混杂机械臂的一体化模型，定义混杂机械臂关节

q = {[\begin{matrix} θ_{1} θ_{2} \dots θ_{6} θ_{7}^{1} θ_{8}^{1} θ_{7}^{2} θ_{8}^{2} θ_{7}^{3} θ_{8}^{3} \end{matrix}]}^{T} \in R^{12 \times 1}

，定义混杂机械臂系统状态为末端夹爪位姿s =

{[\begin{matrix} s_{1}^{T} s_{2}^{T} s_{3}^{T} \end{matrix}]}^{T} \in R^{18 \times 1}

，得到一体化模型为

\dot{s} = J_{A} (q) \dot{q},

(5)

其中J_A（q）∈

R

^18×12为机械臂系统的雅克比矩阵，将 J_A（q）按式（6）进行分块，即

J_{A} (q) = [\begin{matrix} J_{1} \\ J_{2} \\ J_{3} \end{matrix}],

(6)

其中J₁，J₂，J₃分别表示J_A（q）的前6行、中间6行以及后6行，分别为3根柔性夹爪的雅克比矩阵.

取采样时间为T，将模型（5）离散化，即

s (k + 1) = s (k) + J (k) u (k),

(7)

其中: J（k）= T J_A（q）表示刚柔混杂机械臂的离散模型， u（k）=

\dot{q}

表示关节速度，前6个为刚体机械臂关节转动速度，后6个为柔性拉线长度变化速率，满足

q (k) = q (k - 1) + T u (k) .

(8)

4 基于输入映射的柔性夹爪位姿控制

柔性夹爪末端位姿的控制是实现抓取的基础，本节针对该问题进行控制器设计. 由于建模过程中的近似运算，式（7）所表示的模型与实际模型存在偏差，为了削弱模型偏差对系统控制性能产生的影响，增强对柔性夹爪末端位姿的控制，设计了与输入映射数据驱动结合的模型预测控制方法.

4.1 机械臂模型输入映射描述

输入映射是一个数据驱动模块，指的是用历史输入输出数据替换部分系统模型，并且当前的控制输入由历史输入的组合构建而成. 在输入映射框架下，使用长度为l的滑动窗口来收集混杂机械臂系统的历史数据，表示为

\{\begin{matrix} \vec{s} (k - 1) = [\begin{matrix} s (k - 1) & s (k - 2) & \dots & s (k - l) \end{matrix}], \\ \vec{u} (k - 1) = [\begin{matrix} u (k - 1) & u (k - 2) & \dots & u (k - l) \end{matrix}] . \end{matrix}

(9)

由式（7）可得，系统过去l时刻的状态和控制输入的关系为

\{\begin{matrix} s (k) = s (k - 1) + J (k - 1) u (k - 1), \\ s (k - 1) = s (k - 2) + J (k - 2) u (k - 2), \\ ⋮ \\ s (k - l + 1) = s (k - l) + J (k - l) u (k - l), \end{matrix}

(10)

其中J（k − j）（j = 1，2，· · ·，l）为系统在不同历史时刻所对应的模型，系统当前时刻的模型J（k）可由历史时刻模型J（k − j）和一个模型补偿量∆J（k − j）表示，即

J (k) = J (k - j) + Δ J (k - j) .

(11)

在输入映射框架下，定义当前的系统状态由历史系统状态的线性组合和一个额外的状态补偿量构成，即

s (k) = Δ s (k) + \vec{s} (k - 1) λ

(12)

其中: λ = [λ₁ λ₂ · · · λ_l ]^T ∈

R^{l \times 1}

为线性组合系数，∆s（k）∈

R

^18×1为状态补偿量. 同样，可以定义系统当前的控制输入为历史控制输入的线性组合和一个额外的控制补偿量构成，即

u (k) = Δ u (k) + \vec{u} (k - 1) λ,

(13)

其中∆u（k）∈

R

^12×1为控制补偿量.

将式（12）以及式（13）代入系统模型（7），可得下一时刻系统状态为

\begin{matrix} s (k + 1) = Δ s (k) + \vec{s} (k - 1) λ + \\ J (k) (Δ u (k) + \vec{u} (k - 1) λ) = \\ Δ s (k) + J (k) Δ u (k) + \\ (\vec{s} (k - 1) + J (k) \vec{u} (k - 1)) λ, \end{matrix}

(14)

将等式中的

J （ k ） \vec{u} （ k - 1 ）

按式（11）展开，可得到

J (k) [u (k - 1) \dots u (k - l)] =

[J (k - 1) u (k - 1) \dots J (k - l) u (k - l)] +

[Δ J (k - 1) u (k - 1) \dots Δ J (k - l) u (k - l)],

(15)

则可将

\vec{s} （ k - 1 ） + J （ k ） \vec{u} （ k - 1 ）

改写为

\vec{s} (k - 1) + J (k) \vec{u} (k - 1) = [\begin{matrix} s (k - 1) \dots s (k - l)] + \end{matrix}

J (k) [u (k - 1) \dots u (k - l)] = [\begin{matrix} s (k - 1) \dots s (k - l)] + \end{matrix}

[\begin{matrix} J (k - 1) u (k - 1) \dots J (k - l) u (k - l)] + \end{matrix}

[\begin{matrix} Δ J (k - 1) u (k - 1) \dots Δ J (k - l) u (k - l) \end{matrix}] =

[s (k) \dots s (k - l + 1)] +

[Δ J (k - 1) u (k - 1) \dots Δ J (k - l) u (k - l)],

(16)

因此得到式（14）更为紧凑的形式为

s (k + 1) = Δ s (k) + J (k) Δ u (k) + \vec{s} (k) λ + d_{J} λ

(17)

其中

d_{J} = [Δ J (k - 1) u (k - 1) \dots Δ J (k - l) u (k - l)] .

4.2 基于输入映射和MPC的控制器设计

在控制器设计中，由于使用历史数据替换了部分不精确模型，因此，历史数据和控制的反馈机制将在控制器中起主要作用. 考虑到k时刻的控制输入是以式（13）的形式构造的，而对于其他未来时刻的控制输入，仍然采用经典的预测控制策略. 因此，未来N个时刻的带输入映射方法的控制律可以写成

\begin{matrix} U (k) = [(Δ u (k) + \vec{u} (k - 1) λ)^{T} \\ {u^{T} (k + 1) \dots u^{T} (k + N - 1)]}^{T}, \end{matrix}

(18)

输入映射框架下系统在k + 1时刻的状态s（k + 1）如式（17）所示，则系统在k + j（j = 2，3，· · ·，N）时刻的状态为

\{\begin{matrix} s (k) = s (k - 1) + J (k - 1) u (k - 1), \\ s (k - 1) = s (k - 2) + J (k - 2) u (k - 2), \\ ⋮ \\ s (k - l + 1) = s (k - l) + J (k - l) u (k - l), \end{matrix}

(19)

将上述系统在未来时刻的状态写成向量的形式，即

S （ k + 2 ） = F s （ k + 1 ） + Φ （ k ） U （ k + 1 ） .

其中

F = [I_{18} {\begin{matrix} I_{18} \dots I_{18} \end{matrix}]}^{T} \in R^{18 （ N - 1 ） \times 18}

，

\begin{matrix} Φ (k) = \\ [\begin{matrix} J (k) & 0 & \dots & 0 \\ J (k) & J (k) & \dots & 0 \\ ⋮ & ⋮ & ⋮ \\ J (k) & J (k) & \dots & J (k) \end{matrix}] \in R^{18 (N - 1) \times 12 (N - 1)} . \end{matrix}

假设 3根柔性夹爪的期望位姿为

r \in R^{18 \times 1}

和

R \in R^{18 （ N - 1 ） \times 1} ，

，则k时刻下的优化问题可写为

\begin{matrix} m i n Q (k) = \\ ‖ s (k + 1) - r ‖_{W}^{2} + ‖ S (k + 2) - R ‖_{W^{'}}^{2} + \\ ‖ Δ u (k) + λ \vec{u} (k - 1) ‖_{R}^{2} + ‖ U (k + 1) ‖_{R^{'}}^{2}, \\ s . t . ω (k) \in Ω (k), \end{matrix}

(20)

其中: W和W′分别表示当前和未来时刻的位姿权重; R和R′分别表示当前和未来时刻的控制权重. 进行轨迹规划时， r 和R 为期望轨迹，针对抓取任务，r 和 R = [r^T r^T · · · r^T] ^T为被抓物体的抓取位姿点，ω（k）∈Ω（k）表示优化问题的约束，具体定义如下:

\{\begin{matrix} \underline{u} ⩽ u (k) ⩽ \bar{u}, \\ \underline{q} ⩽ q (k - 1) + T u (k) ⩽ \bar{q}, \end{matrix}

(21)

其中:

\underline{u}

，

\bar{u}

表示关节速度限制;

\underline{q}

，

\bar{q}

表示关节角度限制.

优化问题（20）从表面看是二次规划问题的形式，但是

‖ s （ k + 1 ） - r ‖_{Q}^{2} 和 ‖ S （ k + 2 ） - R ‖_{Q^{'}}^{2}

存在不确定项d_J，从而，使该问题无法直接求解，因此，需对其进行转化.

d_J的定义见式（17），表示雅克比矩阵补偿量与关节速度的乘积，反映的是柔性夹爪末端的速度，这在实际系统中存在上界，假设上界为

{\bar{d}}_{J}

. 代入输入映射下k + 1 时刻的系统状态（17），并基于三角不等式原理对

‖ s （ k + 1 ） - r ‖_{Q}^{2}

进行展开，即

\begin{matrix} ‖ s (k + 1) - r ‖_{W}^{2} = \\ {‖Δ s (k) + J (k) Δ u (k) + \vec{s} (k) λ + d_{J} λ - r‖}_{W}^{2} ⩽ \\ ‖ Δ s (k) + J (k) Δ u (k) + \vec{s} λ (k) - r ‖_{W}^{2} + {‖{\bar{d}}_{J} λ‖}_{W}^{2}, \end{matrix}

(22)

同理，对

‖ S （ k + 2 ） - R ‖_{Q^{'}}^{2}

进行展开，即

\begin{matrix} ‖ S (k + 2) - R ‖_{W^{'}}^{2} = \\ ‖ F s (k + 1) + Φ (k) U (k + 1) - R ‖_{W^{'}}^{2} = \\ ‖ F [Δ s (k) + J (k) Δ u (k) + \vec{s} (k) λ + d_{j} λ] + \\ Φ (k) U (k + 1) - R) ‖_{W^{'}}^{2} ⩽ \\ ‖ F [Δ s (k) + J (k) Δ u (k) + \vec{s} (k) λ] ‖_{W^{'}}^{2} + \\ ‖ Φ (k) U (k + 1) - R ‖_{W^{'}}^{2} + {‖F {\bar{d}}_{J} λ‖}_{W^{'}}^{2}, \end{matrix}

(23)

那么，综合不等式（22）–（23），可得到

\begin{matrix} Q (k) ⩽ ‖ Δ s (k) + J (k) Δ u (k) + \vec{s} (k) λ - r ‖_{W}^{2} + \\ {‖{\bar{d}}_{J} λ‖}_{W}^{2} + ‖ F [Δ s (k) + J (k) Δ u (k) + \\ \vec{s} (k) λ] ‖_{W^{'}}^{2} +‖ Φ (k) U (k + 1) - R ‖_{W^{'}}^{2} + \\ {‖F {\bar{d}}_{J} λ‖}_{W^{'}}^{2} + ‖ Δ u (k) + \vec{u} (k - 1) λ ‖_{R}^{2} + \\ ‖ U (k + 1) ‖_{R^{'}}^{2} = \bar{Q} (k), \end{matrix}

(24)

此外，考虑到λ的系数矩阵可能出现半正定的情况，因此加入额外正定项

‖ λ ‖_{ϵ}^{2}

来保证λ的系数矩阵正定. 最终得到优化问题为

\begin{matrix} \underset{Δ u (k), λ, U (k + 1)}{m i n} Q^{'} (k) = \bar{Q} (k) + ‖ λ ‖_{ϵ}^{2}, \\ s . t . ω (k) \in Ω (k), \end{matrix}

(25)

其中:

ϵ \in R^{l \times l}

为λ的权重矩阵; ∆u（k），U（k + 1）和 λ为优化变量，可通过求解标准二次规划问题（25）得到.

基于上述设计，可将刚柔混杂机械臂的柔性夹爪控制算法归纳如下:

步骤 1 测量系统初始状态s（0），初始化滑动窗口

\vec{x} （ 0 ） ， \vec{x} （ 1 ） ， \vec{u} （ 0 ）

;

步骤 2 控制时刻从k = 1开始;

步骤 3 在k时刻，根据式（7）计算系统模型;

步骤 4 由预定义期望轨迹或相机得到被抓取物体的位姿，得到期望姿态点r和R;

步骤 5 通过求解优化问题（25），得到系统优化变量∆u（k），U（k + 1）和λ;

步骤 6 由式（13）计算当前时刻控制量u（k）;

步骤 7 由式（8）计算当前关节角并发给混杂机械臂执行并测量s（k + 1）;

步骤 8 将s（k），s（k + 1）， u（k）分别存入滑动窗口向量

\vec{s} （ k ） ， \vec{s} （ k + 1 ） 和 \vec{u} （ k ）

中;

步骤 9 令k = k + 1，转到步骤3.

4.3 基于物体姿态的柔性夹爪抓取算法

上文对刚柔混杂机械臂的控制器进行了设计，实现对柔性末端位姿的控制，这是实现抓取算法的基础. 为了准确获取被抓物体的姿态信息，以确定抓取路径，本文采用ArUco码方块作为被抓物体，方块每个面对应不同的ArUco序列号. 通过视觉伺服，可以确定检测到的ArUco码的姿态和序列号信息，从而，解决了被抓物体姿态估计的问题.

基于被抓物体的姿态，将抓取分为精确抓取和包络抓取. 当物体较为平稳或者需要特定位置精确操作时，通过计算最佳抓取点，控制柔性夹爪末端位姿来实现精确抓取. 当物体的姿态不平稳或者物体形状不规则，难以确定精确抓取点时采用包络抓取. 包络抓取通过机器人的手部形成一个包围圈，从而，抓住物体，这种方法对姿态和精确位置的依赖较小.

本文选取方块的上表面对其姿态进行分析，判断方块的放置是否平稳. 在视觉伺服下，通过手眼标定，将上表面姿态转换到机械臂基坐标系下描述，用a = [ψ_a ϑ_a φ_a]，其中ψ_a，ϑ_a，φ_a分别表示上表面坐标系绕机械臂基坐标系x，y，z轴转动的角度. 上表面坐标系的z轴与基坐标系的z轴保持一致，即竖直向上时，可认为方块处于平稳状态，而上表面z轴与竖直方向的偏差可由ψ_a和ϑ_a反映（绕x和y轴转动时才会改变z轴方向），因此可定义如下判断方程式:

{(ψ_{a})}^{2} + {(ϑ_{a})}^{2} < t_{a},

(26)

其中t_a为设定的阈值，当不等式（26）成立时，方块为平稳状态，进行精确抓取，否则进行包络抓取. 包络抓取时，首先，将柔性夹爪的中心移动到位于被抓取物体中心的上方，并保持夹爪朝下; 然后，打开夹爪，保持打开动作向下移动直到夹爪将物体包裹; 最后，关闭夹爪完成抓取.

进行精确抓取的前提是抓取点的计算，计算抓取点时所需参数如图3所示. p₁，p₂，p₃为3个抓取点，包含位置和姿态信息; θ_1，2，θ_1，3，θ_2，3是3个抓取点与物体中心连线的夹角; β₁，β₂，β₃是连线与抓取面法线的夹角. 从被抓物体的角度出发，需要考虑两方面. 一是抓取点尽可能均匀分布，保持在120^◦为佳，可使得物体受力均匀，从而，提高抓取的稳定性和可靠性. 二是抓取点的方向应尽可能与抓取平面的法线方向一致，这是为了最大化夹爪与被抓物体的接触面积，可更好地传递抓取力. 基于上述分析，本节设置360个抓取点，每个抓取点的方向指向物体中心以确保力的闭合，同时，构建如式（27）的基于最优抓取点的优化问题:

\begin{matrix} Q_{1} = k_{1} (\frac{2}{3} π - m i n (|θ_{1,2}|, |θ_{1,3}|, |θ_{2,3}|)) + \\ k_{2} m a x (|β_{1}|, |β_{2}|, |β_{3}|), \end{matrix}

(27)

其中，k₁ >0，k₂ >0，表示两部分的权重. 此外，通过优化柔性夹爪的初始位置与抓取点的一致性，可以减少在抓取过程中需要的调整次数，从而提高操作的效率和流畅性. 假设夹爪的初始姿态为ϕ₁，ϕ₂，ϕ₃，改写优化问题（27）为

Q_{2} = ϵ_{1} Q_{1} + ϵ_{2} \sum_{i = 1}^{3} ({‖ϕ_{i} - a_{i}‖}_{2}),

(28)

其中: ϵ₁ >0，ϵ₂ >0，a_i（i= 1，2，3）为p_i中的姿态向量，

‖ v ‖_{2}

表示向量v的二范数.

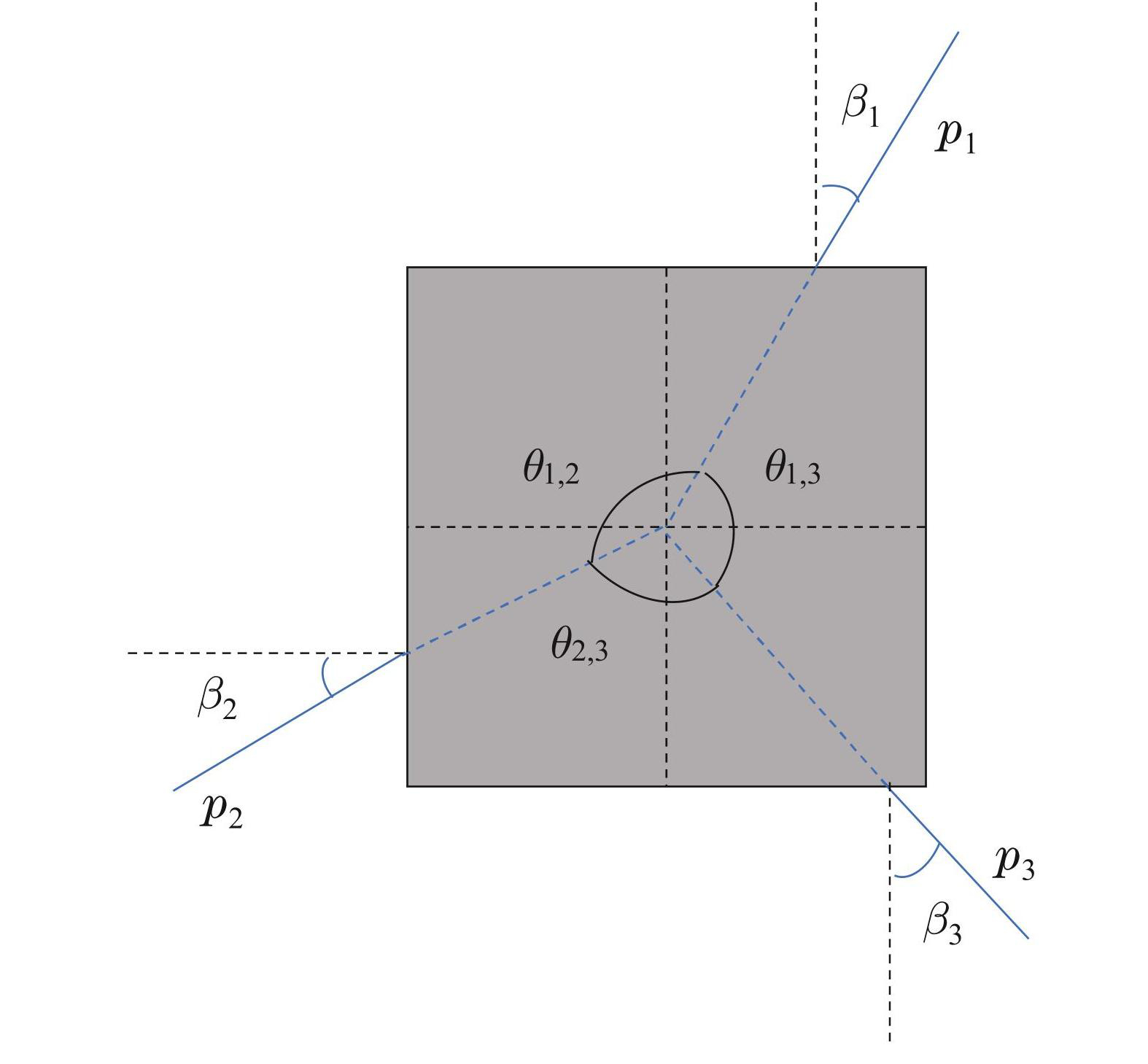
图3被抓物体抓取点参数

Fig.3Parameters of the grasping points for the grasped object

将抓取平面分成360部分，并根据机械臂夹爪末端的姿态和待抓取物体的姿态求解优化问题（28），完成抓取点的计算，在此基础上完成精确抓取. 可将物体抓取算法归纳如下:

步骤 1 测量柔性夹爪初始姿态ϕ₁，ϕ₂，ϕ₃，由式（26）判断物体是否平稳，选择抓取方法;

步骤 2 若为精确抓取，由式（28）计算抓取点，否则进行包络抓取;

步骤 3 将夹爪移到被抓物体正上方，保持夹爪向下并打开夹爪;

步骤 4 若为精确抓取，由计算得到的抓取点进行路径规划，否则进行包络抓取规划;

步骤 5 求解优化问题（25），执行抓取过程;

步骤 6 完成抓取.

5 多指柔性夹爪的控制及抓取实验

本节先通过MATLAB平台仿真，通过柔性夹爪末端直线轨迹跟踪验证了基于输入映射和MPC的末端位姿控制方法的有效性，进而在搭建的多指刚柔混杂机械臂硬件平台上进行精确抓取和包络抓取实验，验证了抓取算法的有效性.

5.1 输入映射位姿控制仿真验证

为了验证本文提出的基于输入映射和模型预测控制方法对柔性夹爪位姿控制的有效性，本节针对该方法与MPC ^[31] 及自适应模型预测控制（adaptive model predictive control，AMPC）^[32] 进行轨迹跟踪仿真对比实验，并将本文提出的方法命名为IMMPC（input map-ping model predictive control）.

针对上述3种情形，仿真控制时域、权重矩阵、机械臂关节速度约束以及角度约束等参数保持一致，如表1所示.

表1位姿控制仿真实验参数

Table1Simulation parameters for pose control

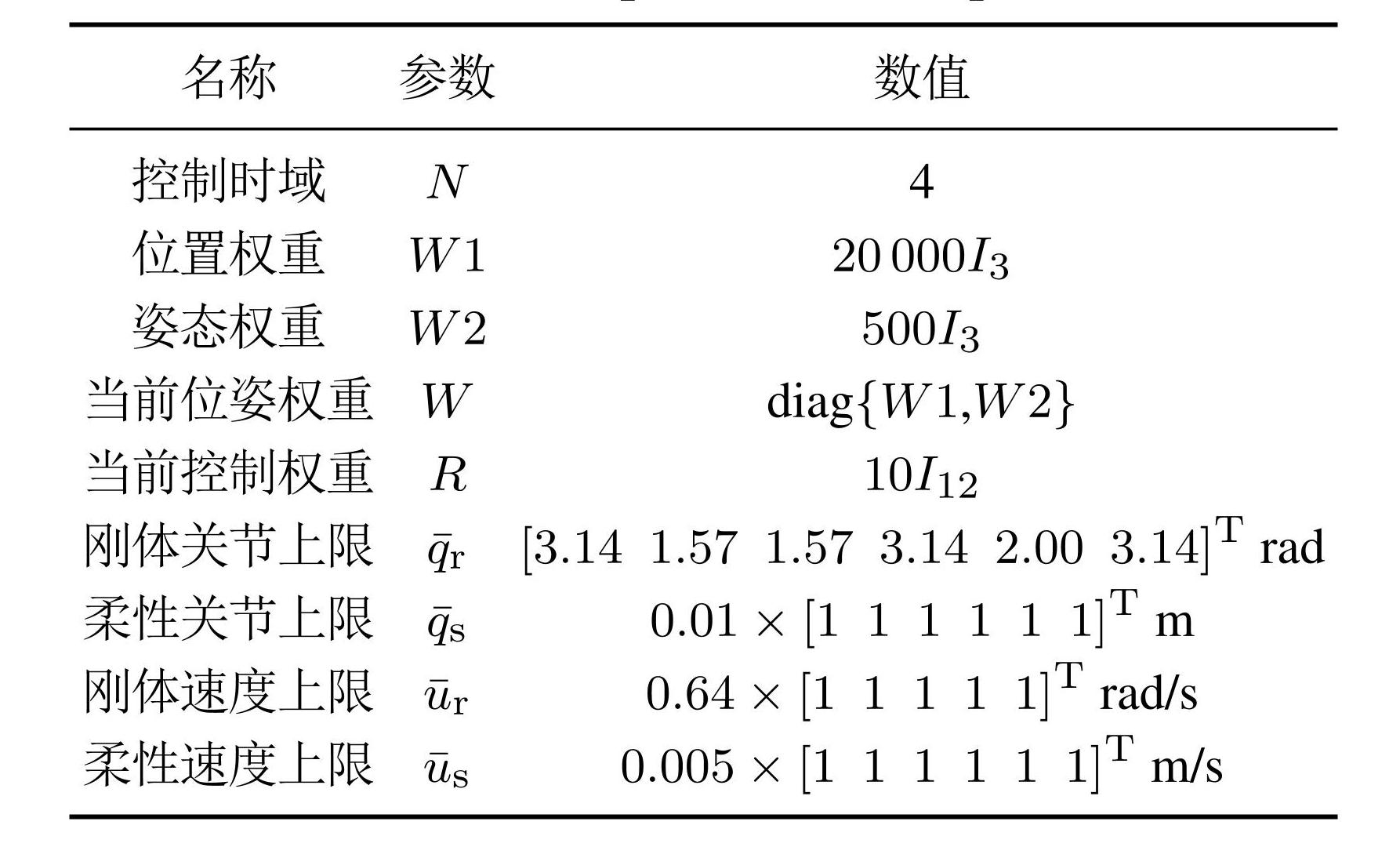
刚体机械臂关节角度下限

{\underline{q}}_{r} = - {\bar{q}}_{r}

，关节速度下限

{\underline{u}}_{r} = - {\bar{u}}_{r}

. 柔性夹爪关节角度下限

{\underline{q}}_{s} = - {\bar{q}}_{s}

，关节速度下限

{\underline{u}}_{s} = - {\bar{u}}_{s}

. 未来位姿权重矩阵 W′ = 0.5 × diag {W，W，· · ·，W} ∈

R^{18 （ N - 1 ） \times 18 （ N - 1 ）}

，未来控制权重矩阵 R′ = 0.5 × diag {R，R，· · ·， R} ∈

R^{12 （ N - 1 ） \times 12 （ N - 1 ）}

. 在 IMMPC方法中，滑动窗口长度 l设置为3.

在3组对比仿真实验中，将关节为零的状态设为机械臂初始状态，表示为s_init =

= {[\begin{matrix} s_{init 1}^{T} s_{init 2}^{T} s_{init 3}^{T} \end{matrix}]}^{T}

，其中:

\begin{matrix} s_{init 1} = {[\begin{matrix} 0.025 & - 0.04 & 0.78 & 0.00 & 0.00 & 2.09 \end{matrix}]}^{T}, \\ s_{init 2} = {[\begin{matrix} 0.025 & - 0.04 & 0.78 & 0.00 & 0.00 & - 2.09 \end{matrix}]}^{T}, \\ s_{init 3} = {[\begin{matrix} - 0.05 & 0.00 & 0.78 & 0.00 & 0.00 & 2.09 \end{matrix}]}^{T}, \end{matrix}

期望位姿为

J_{d e s} = {[\begin{matrix} s_{d e s 1}^{T} s_{d e s 2}^{T} s_{d e s 3} \end{matrix}]}^{T}

，其中:

\begin{matrix} s_{d e s 1} = {[\begin{matrix} 0.40 & 0.13 & 0.53 & - 0.55 & 0.62 & - 1.75 \end{matrix}]}^{T}, \\ s_{d e s 2} = {[\begin{matrix} 0.38 & 0.09 & 0.53 & 0.53 & 0.71 & 0.96 \end{matrix}]}^{T}, \\ s_{d e s 3} = {[\begin{matrix} 0.41 & 0.10 & 0.51 & 0.03 & 0.02 & 2.75 \end{matrix}]}^{T} . \end{matrix}

针对每根柔性夹爪，在初始和期望位姿之间进行路径插值，其中，位置部分采用直线插值，同时，为了保证柔性夹爪末端姿态的顺利过渡，姿态部分采用四元素球面插值，最后，得到每根柔性夹爪各自的插值轨迹，即

\begin{matrix} {p a t h}_{i}^{j} = T r a j (s_{initi}, s_{desi}), \\ i = 1,2, 3, j = 1,2, \dots, M, \end{matrix}

(29)

Traj为轨迹插值函数，M为轨迹点数量. 使用IMMPC 方法控制时柔性夹爪末端和期望轨迹的曲线如图4所示，实线为期望轨迹，虚线为柔性末端轨迹.

跟踪期望轨迹的第j个点时柔性夹爪末端的位姿为

s_{c u r 1}^{j} ， s_{c u r 2}^{j} ， s_{c u r 3}^{j}

，当前跟踪点为

{p a t h}_{1}^{j} ， {p a t h}_{2}^{j} ， {p a t h}_{3}^{j}

，为了比较IMMPC，AMPC和MPC方法的性能，计算每根柔性夹爪末端的实际位姿与期望位姿之差，计算公式为式（30），同时，按照式（31）计算3根柔性夹爪的误差之和，3种方法的误差和曲线如图5所示.

\begin{matrix} {e r r o r}_{i}^{j} = ‖ s_{curi}^{j} - {path}_{i}^{j} ‖_{2}, \\ i = 1,2, 3, j = 1,2, \dots, M, \end{matrix}

(30)

{error}^{j} = \sum_{i = 1}^{3} {e r r o r}_{i}^{j}, j = 1,2, \dots, M .

(31)

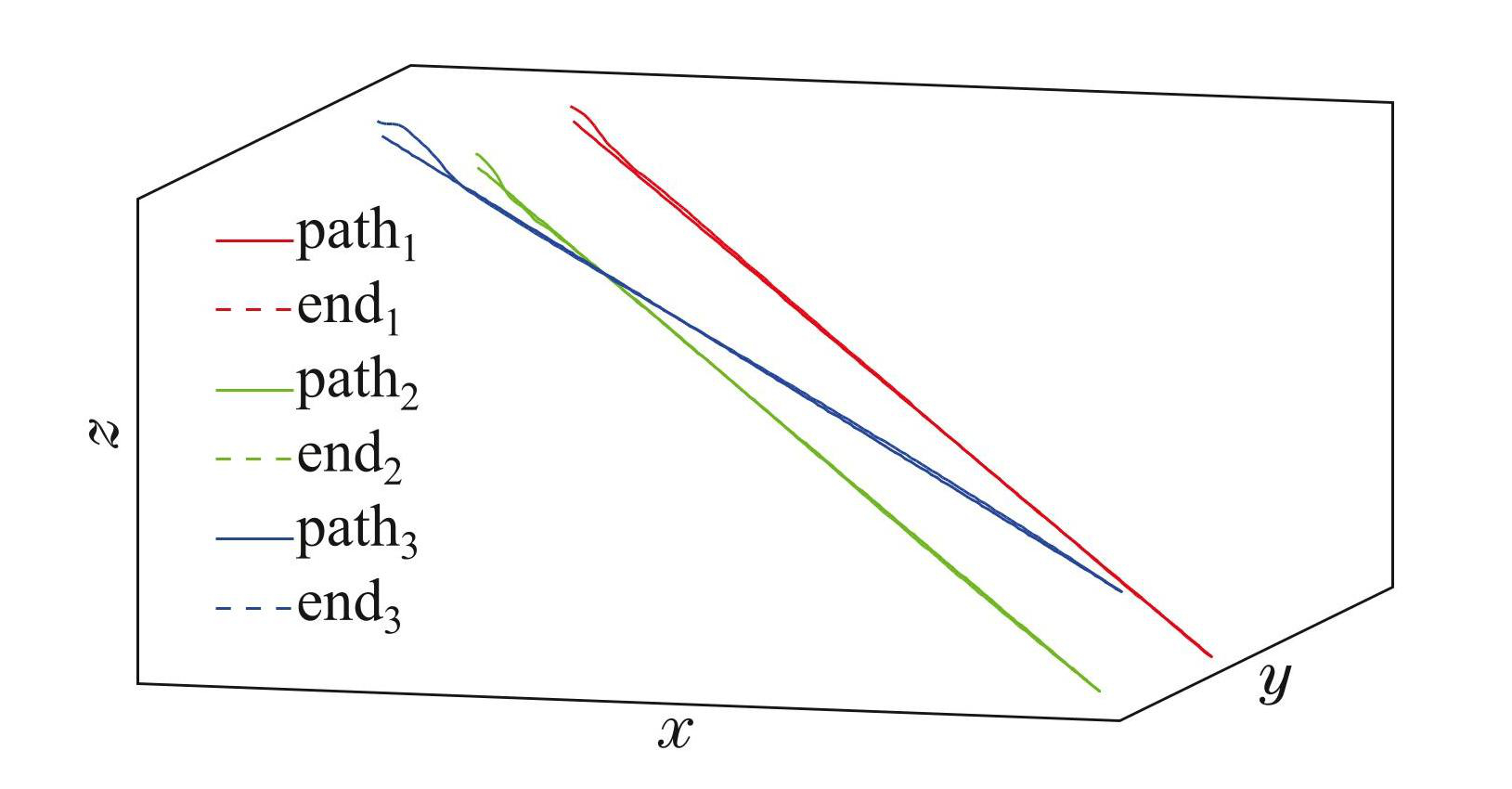
图4IMMPC方法的末端轨迹曲线和参考轨迹曲线

Fig.4The end trajectory curves and reference trajectory curves of the IMMPC method

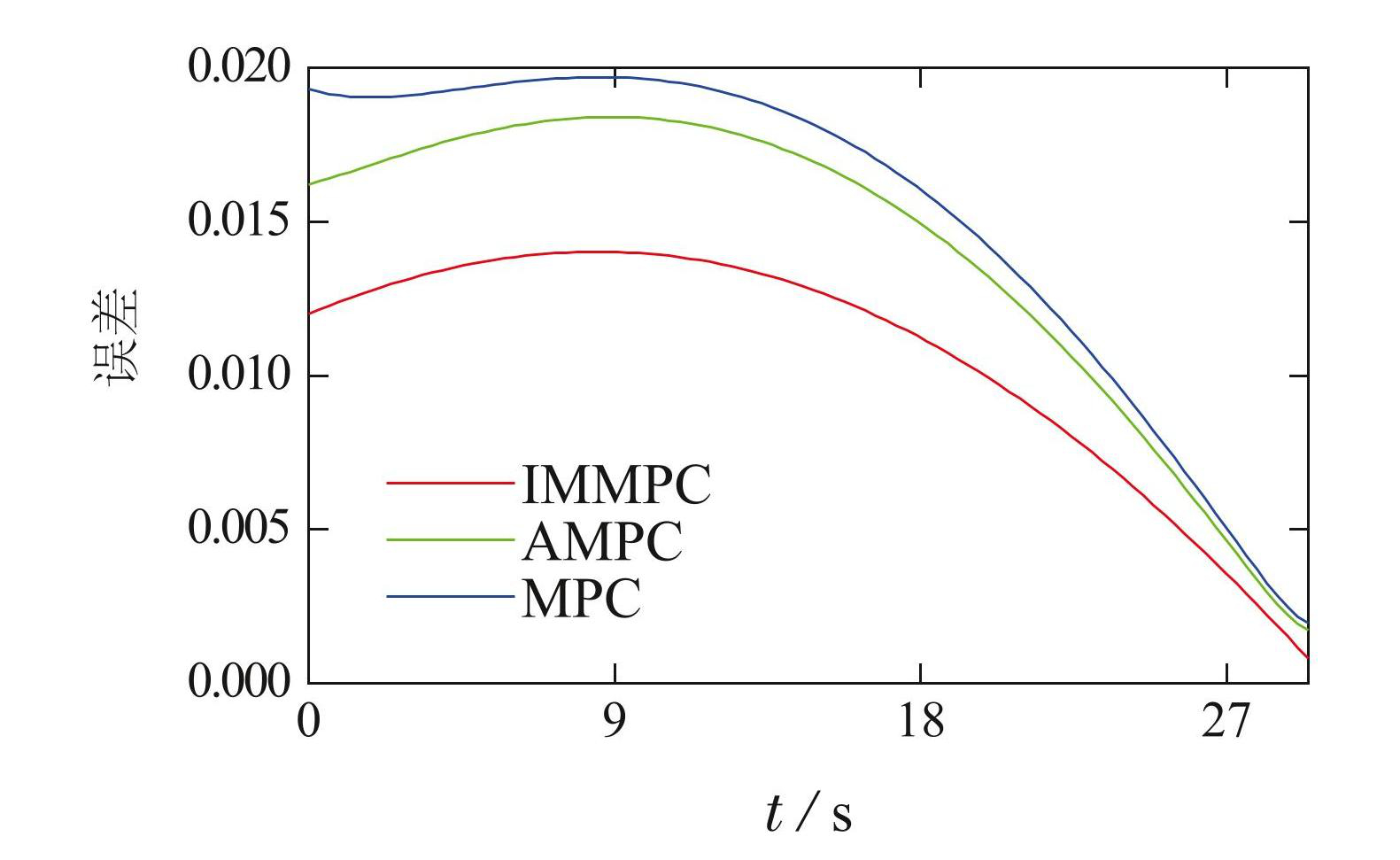
图5不同方法的柔性夹爪轨迹跟踪误差

Fig.5Pose error between end-effector and reference trajectory of different methods

从图5可见，IMMPC方法在柔性夹爪末端位姿控制中的误差最小，表现最佳，其次是AMPC方法，MPC 控制性能最差. 在运动过程中，AMPC通过控制器存储的数据提升模型精度，改善控制性能，因此，收敛性优于MPC. 而IMMPC利用有限滑动窗口收集近期数据并直接补偿控制器性能，无需大量数据即可迅速提升控制效果. 此外，当滑动窗口长度l为0时，控制器退化为普通MPC. 若l过大，则会产生信息冗余并增加计算负担，因此，实验中将l设置为3.

5.2 实物抓取实验

如表1所示，抓取实验的权重矩阵、控制时域、滑动窗口长度等参数均与仿真一致，基于ArUco方块摆放的姿态，分别使用精确抓取和包络抓取对其进行抓取，此外，机械臂的初始状态与仿真的初始状态一致，均为s_init.

抓取中，根据抓取算法，计算机获取抓取物体的位姿信息，由式（26）判断物体是否平稳，从而，选择相应的抓取方式. 若为精确抓取，首先，根据机械臂初始状态sinit计算精确抓取点，然后，利用基于输入映射和 MPC的位姿控制器完成整个抓取动作，精确抓取过程和包络抓取过程分别如图6–7所示.

图6精确抓取流程图

Fig.6Precise grasping process diagram

图7包络抓取流程图

Fig.7Envelop grasping process diagram

以精确抓取为例，流程图的前两帧，机械臂检测到物体位姿，选择精确抓取，计算抓取点并将夹爪移动到被抓物体正上方准备抓取; 第3第4帧中，机械臂打开夹爪抓取物体，最后两帧将物体抓取并放置在桌面上. 抓取过程中刚柔混杂机械臂的关节速度和关节角度分别如图8–9所示.

从精确抓取的速度图和关节图中可以看出，在初始时刻，大约在前30 s，机械臂根据检测到的物体位置移动到物体正上方，此时主要是刚体机械臂的关节提供大范围运动; 大约30 s到40 s时柔性夹爪打开，并在 40 s到50 s之间保持打开动作，同时，柔性夹爪向下准备抓取物体; 50 s到60 s时夹爪闭合对物体进行精确抓取，60 s到70 s柔性夹爪尽量保持闭合状态并将物体平稳抓取，之后，机械臂打开柔性夹爪将物体放置在桌面上. 此外，从关节角度图中可以看出在初始时刻以及约在70 s时，刚体机械臂和柔性夹爪的速度达到最大值，刚体机械臂最大速度为 0.64 rad/s，柔性夹爪最大速度为0.005 m/s. 此外，从关节角度图可知，刚柔机械臂的角度始终在安全范围内，柔性夹爪最大角度达到0.01 m，满足表1所列的关节速度和角度约束条件. 在控制算法方面，本文提出的控制器结合了输入映射数据驱动方法与MPC方法的优势，能够在无需精确系统模型的情况下，精准地控制柔性夹爪末端到达预期位姿. 在精确抓取和包络抓取实验中，柔性夹爪成功将物体夹取并放置在指定位置，证实了抓取算法的有效性.

图8精确抓取关节速度

Fig.8Joint speed in precise grasping

图9精确抓取关节角度

Fig.9Joint position in precise grasping

6 结论

本文针对传统刚性机械臂抓取过程中与环境交互不安全的问题，搭建了多指刚柔混杂机械臂抓取平台，分别使用旋量理论和分段常曲率方法对刚体和柔性部分进行建模. 基于混杂机械臂的模型，提出了基于输入映射的数据驱动和MPC控制算法，输入映射的作用主要有两处，一是利用历史数据替换系统部分不精确的模型，从而，削弱不精确模型对控制性能的影响; 二是利用历史数据的线性组合来构造当前时刻的控制输入，柔性夹爪轨迹跟踪仿真实验表明该控制算法能够精确控制柔性夹爪末端的位姿到达期望位姿. 后续在该控制算法的基础上设计了精确抓取和包络抓取算法，抓取方式的选择是根据被抓物体的姿态确定的，并在精确抓取中设计了抓取点的最优选择方法. 最后，通过实物抓取实验验证了这两种抓取算法的有效性. 然而，本文所设计的算法仍存在一些局限性. 例如控制器在应对外部扰动时的鲁棒性策略尚需完善; 在复杂动态环境中的机械臂避障策略尚未探讨; 柔性夹爪末端的柔顺控制也有研究的必要; 此外，与深度学习控制方法的结合也是未来需要进一步改进的方向.

图1柔性夹爪结构设计

Fig.1The structure design of the soft robot

下载: 全尺寸图片

图2刚柔混杂机械臂抓取平台

Fig.2The grasping platform of rigid-soft robot

下载: 全尺寸图片

图3被抓物体抓取点参数

Fig.3Parameters of the grasping points for the grasped object

下载: 全尺寸图片

图4IMMPC方法的末端轨迹曲线和参考轨迹曲线

Fig.4The end trajectory curves and reference trajectory curves of the IMMPC method

下载: 全尺寸图片

图5不同方法的柔性夹爪轨迹跟踪误差

Fig.5Pose error between end-effector and reference trajectory of different methods

下载: 全尺寸图片

图6精确抓取流程图

Fig.6Precise grasping process diagram

下载: 全尺寸图片

图7包络抓取流程图

Fig.7Envelop grasping process diagram

下载: 全尺寸图片

图8精确抓取关节速度

Fig.8Joint speed in precise grasping

下载: 全尺寸图片

图9精确抓取关节角度

Fig.9Joint position in precise grasping

下载: 全尺寸图片

表1位姿控制仿真实验参数

Table1Simulation parameters for pose control

下载: 全尺寸图片

图1柔性夹爪结构设计

Fig.1The structure design of the soft robot

图2刚柔混杂机械臂抓取平台

Fig.2The grasping platform of rigid-soft robot

图3被抓物体抓取点参数

Fig.3Parameters of the grasping points for the grasped object

图4IMMPC方法的末端轨迹曲线和参考轨迹曲线

Fig.4The end trajectory curves and reference trajectory curves of the IMMPC method

图5不同方法的柔性夹爪轨迹跟踪误差

Fig.5Pose error between end-effector and reference trajectory of different methods

图6精确抓取流程图

Fig.6Precise grasping process diagram

图7包络抓取流程图

Fig.7Envelop grasping process diagram

图8精确抓取关节速度

Fig.8Joint speed in precise grasping

图9精确抓取关节角度

Fig.9Joint position in precise grasping

表1位姿控制仿真实验参数

Table1Simulation parameters for pose control

图1柔性夹爪结构设计

Fig.1The structure design of the soft robot

图2刚柔混杂机械臂抓取平台

Fig.2The grasping platform of rigid-soft robot

图3被抓物体抓取点参数

Fig.3Parameters of the grasping points for the grasped object

图4IMMPC方法的末端轨迹曲线和参考轨迹曲线

Fig.4The end trajectory curves and reference trajectory curves of the IMMPC method

图5不同方法的柔性夹爪轨迹跟踪误差

Fig.5Pose error between end-effector and reference trajectory of different methods

图6精确抓取流程图

Fig.6Precise grasping process diagram

图7包络抓取流程图

Fig.7Envelop grasping process diagram

图8精确抓取关节速度

Fig.8Joint speed in precise grasping

图9精确抓取关节角度

Fig.9Joint position in precise grasping

表1位姿控制仿真实验参数

Table1Simulation parameters for pose control

ZHOU C, LEI M, ZHAO L,et al. TOPP-MPC-based dual-arm dynamic collaborative manipulation for multi-object nonprehensile transportation. International Conference on Robotics and Automation(ICRA). Philadelphia, America: IEEE,2022:999-1005.

LUO J, ZHONG X, SHI C,et al. Estimation of 7-DoF robot grasp pose of unknown objects in stacking scenes.42nd Chinese Control Conference(CCC). Tianjin, China: IEEE,2023:4388-4393.

LIU M, HONG Y, DENG L. Research on data construction and classification of deformable objects grasped by soft hand with multi-source information fusion.34th Chinese Control and Decision Conference(CCDC). Hefei, China: IEEE,2022:6272-6276.

ZHAO X, ZHANG Y, DING W,et al. A dual-arm robot cooperation framework based on a nonlinear model predictive cooperative control. IEEE/ASME Transactions on Mechatronics,2023,29(5):3993-4005.

PAROSI R, RISIGLIONE M, CALDWELL D G,et al. Kinematically-decoupled impedance control for fast object visual servoing and grasping on quadruped manipulators. IEEE/RSJ International Conference on Intelligent Robots and Systems(IROS). Detroit, Michigan, American: IEEE,2023:1-8.

SUN Xiantao, TANG Siyu, CHEN Wenjie,et al. Target object grasp based on push-grasp cooperative operation in complex environment. Control Theory & Applications,2023,40(10):1713-1720.(孙先涛, 唐思宇, 陈文杰, 等. 复杂环境下基于推抓协同操作的目标物体抓取. 控制理论与应用,2023,40(10):1713-1720.)

SHE Y, LIU S Q, YU P,et al. Exoskeleton-covered soft finger with vision-based proprioception and tactile sensing. IEEE International Conference on Robotics and Automation(ICRA). Paris, France: IEEE,2020:10075-10081.

ZHANG Xiao, ZHANG Qiuju. Research on optimal grasping planning based on flexible wrist-hand. Chinese Journal of Engineering Design,2020,27(3):307-316.(张潇, 张秋菊. 基于柔性腕手的最优抓取规划研究. 工程设计学报,2020,27(3):307-316.)

HU Y, LI J, CHEN Y,et al. Design and control of a highly redundant rigid-flexible coupling robot to assist the COVID-19 oropharyngealswab sampling. IEEE Robotics and Automation Letters,2021,7(2):1856-1863.

PFEIFER R, LUNGARELLA M, IIDA F. The challenges ahead for bio-inspired’soft’robotics. Communications of the ACM,2012,55(11):76-87.

MAJIDI C. Soft robotics: A perspective-current trends and prospects for the future. Soft Robotics,2014,1(1):5-11.

WEBSTER R J, JONES B A. Design and kinematic modeling of constant curvature continuum robots: A review. The International Journal of Robotics Research,2010,29(13):1661-1683.

DELLA S C, BICCHI A, RUS D. On an improved state parametrization for soft robots with piecewise constant curvature and its use in model based control. IEEE Robotics and Automation Letters,2020,5(2):1001-1008.

COEVOET E, MORALES-BIEZE T, LARGILLIERE F,et al. Software toolkit for modeling,simulation,and control of soft robots. Advanced Robotics,2017,31(22):1208-1224.

ARMANINI C, HUSSAIN I, IQBAL M Z,et al. Discrete cosserat approach for closed-chain soft robots: Application to the fin-ray finger. IEEE Transactions on Robotics,2021,37(6):2083-2098.

ARMANINI C, BOYER F, MATHEW A T,et al. Soft robots modeling: A structured overview. IEEE Transactions on Robotics,2023,39(3):1728-1748.

JONES B A, WALKER I D. Kinematics for multisection continuum robots. IEEE Transactions on Robotics,2006,22(1):43-55.

DAVIDSON J K, HUNT K H, PENNOCK G R. Robots and screw theory: Applications of kinematics and statics to robotics. Journal of Mechanical Design,2004,126(4):763-764.

YANG Yan, LIU Zhijie, HAN Jiangtao,et al. Overview of actuators,modeling,and control methods for soft manipulators. Chinese Journal of Engineering,2022,44(12):2124-2137.(杨妍, 刘志杰, 韩江涛, 等. 柔性夹爪的驱动方式、建模与控制研究进展. 工程科学学报,2022,44(12):2124-2137.)

RUNXI Z, HESHENG W, WEIDONG C. Shape control for a soft robot inspired by octopus. Robot,2016,38(6):754-759.

WANG H, ZHANG R, CHEN W,et al. Shape detection algorithm for soft manipulator based on fiber bragg gratings. IEEE/ASME Transactions on Mechatronics,2016,21(6):2977-2982.

WANG H, WANG C, CHEN W,et al. Three-dimensional dynamics for cable-driven soft manipulator. IEEE/ASME Transactions on Mechatronics,2016,22(1):18-28.

CHEN J, DENG H, CHAI W,et al. Manipulation task simulation of a soft pneumatic gripper using ros and gazebo. IEEE International Conference on Real-time Computing and Robotics(RCAR). Kandima, Maldives: IEEE,2018:378-383.

XU W, HU Z, YAN L,et al. Modeling and planning of a space robot for capturing tumbling target by approaching the dynamic closest point. Multibody System Dynamics,2019,47:203-241.

LI Jian, HUANG Meizhen, YAN Jie,et al. Simulation and experiment of SMA-wire assisted pneumatic variable-stiffness actuator. Journal of Machine Design,2023,40(3):32-40.(李健, 黄美珍, 闫杰, 等. SMA丝辅助气动变刚度驱动器仿真与实验. 机械设计,2023,40(3):32-40.)

XU F, WANG H, LIU Z,et al. Adaptive visual servoing for an underwater soft robot considering refraction effects. IEEE Transactions on Industrial Electronics,2019,67(12):10575-10586.

XU W, LIU T, LI Y. Kinematics,dynamics,and control of a cabledriven hyper-redundant manipulator. IEEE/ASME Transactions on Mechatronics,2018,23(4):1693-1704.

CUI Chaochen, ZHANG Xiang, XIONG Dan,et al. Two-stage neural network control method for space soft manipulator. Control Theory & Applications,2023,40(12):2257-2264.(崔朝臣, 张翔, 熊丹, 等. 空间柔性夹爪的两阶段神经网络控制方法. 控制理论与应用,2023,40(12):2257-2264.)

WU Q, GU Y, LI Y,et al. Position control of cable-driven robotic soft arm based on deep reinforcement learning. Information,2020,11(6):310.

HE S, SUN L, XU Y,et al. A modeling and data-driven control framework for rigid-soft hybrid robot with visual servoing. IEEE Robotics and Automation Letters,2023,8(11):7281-7288.

TANG Q, CHU Z, QIANG Y,et al. Trajectory tracking of robotic manipulators with constraints based on model predictive control. International Conference on Ubiquitous Robots, Xi’an, China: IEEE,2020:23-28.

ZHU B, ZHENG Z, XIA X. Constrained adaptive model-predictive control for a class of discrete-time linear systems with parametric uncertainties. IEEE Transactions on Automatic Control,2019,65(5):2223-2229.