欢迎访问《控制理论与应用》期刊网站！

基于MESEN的机械臂运动预测控制

doi: 10.7641/CTA.2025.40369

平梦玲，刘斌，何芳，刘德旺，余梦琪

南昌航空大学信息工程学院, 江西南昌 330063

基金项目: 国家自然科学基金项目(61963030), 江西省教育厅科技项目(GJJ2401012)资助.

详细信息

作者简介

平梦玲硕士研究生,目前研究方向为约束预测控制在机械臂控制方面的应用,E-mail: 1807251132@qq.com;

刘斌教授,研究生导师,目前研究方向为预测控制理论及方法,E-mail: 1248302751@qq.com;

何芳硕士研究生,目前研究方向为智能机器人的轨迹跟踪控制,E-mail: 3190561589@qq.com;

刘德旺硕士研究生,目前研究方向为约束预测控制在机械臂控制方面的应用,E-mail: 18379953422@163.com;

余梦琪硕士研究生,目前研究方向为自适应控制及其应用,E-mail: 1434156960@qq.com.

通信作者

刘斌，E-mail: 1248302751@qq.com;Tel.:+86791-83863741

Predictive control of robotic arm motion based on MESEN

PING Meng-ling ， LIU Bin ， HE Fang ， LIU De-wang ， YU Meng-qi

Information Engineering Institute, Nanchang Hangkong University, Nanchang Jiangxi 330063 , China

Funds: Supported by the National Natural Science Foundation of China (61963030) and the Jiangxi Provincial Department of Education Science and Technology Program (GJJ2401012).

摘要

针对机械臂运动控制问题, 首先建立与实体机械臂对应的DH参数表以及运动学方程, 其次利用运动学设计机械臂的位置预测控制器, 然后针对控制器模型的凸优化问题, 引入终端代价及终端约束, 采用增强型迭代模型预测控制策略来实现多轴机械臂运动控制. 并采用误差求和增强型牛顿法来提升滚动优化过程中的迭代效率. 此外, 还提出了一种MESEN算法, 通过有效控制算法步长以及模型中相关系数的大小, 进一步提高系统的收敛速度, 减少优化过程对系统初始偏差的依赖. 最后, 利用Lyapunov定理对MESEN算法的收敛性进行分析, 并对六轴机械臂进行实验验证. 实验结果表明, 所提算法在大规模约束的模型中具有较好的效果.

关键词

机械臂运动控制 / 凸优化 / 模型预测控制 / MESEN

Abstract

Aiming at the motion control problem of the manipulator, first, the DH parameter table and kinematic equation corresponding to the physical manipulator are established. Then, a position predictive controller of the manipulator is designed using kinematics. Subsequently, to address the convex optimization problem of the controller model, the terminal cost and terminal constraints are introduced, and the enhanced iterative model predictive control strategy is employed to achieve the motion control of the multi-axis manipulator. The Error-Summing Enhanced Newton algorithm is used to improve the iterative efficiency in the rolling optimization process. In addition, a MESEN algorithm is proposed which further improves the convergence speed of the system and reduces the dependence of the optimization process on the initial system deviation by effectively controlling the step size of the algorithm and the correlation coefficient in the model. Finally, the convergence of the MESEN algorithm is analyzed using Lyapunov’s theorem, and the six-axis manipulator is simulated and verified. Experimental results show that the proposed algorithm performs well in the large-scale constrained model.

Keywords

robotic arm motion control / convex optimization / model predictive control / MESEN

1 引言 2 机械臂运动学模型 3 位置控制器的设计 4 基于MPC的MESEN在线求解 4.1 凸优化问题 4.2 建立MESEN模型 4.3 MESEN算法收敛性分析 5 实验结果与分析 5.1 仿真对比 5.2 物理平台实验 6 结论

1 引言

工业生产自动化推进机械臂在工业领域的广泛应用，串联型机械臂在面对复杂任务时，自由度会随着关节数的增加而增加，导致机械臂关节旋转角度的限制和避碰的范围增大 ^[1] . 针对上述问题，如何建立机械臂模型以及如何控制机械臂运动逐渐成为研究中的重点. 机械臂运动规划包含路径规划和轨迹优化 ^[2-4]，运动规划的核心问题是通过已知条件求解逆运动学的问题，针对该问题，世界各国也正在积极探索多轴机械臂路径控制和优化方法 ^[5-6] . 根据规划范围还可以分为局部和全局路径规划 ^[7-8] . 其中，局部路径规划主要针对机械臂当前作业的局部空间信息，具有良好的动态规划性能，对噪声干扰大的环境有较强的鲁棒性，但对机械臂硬件要求较高且缺乏全局环境信息导致规划结果不佳; 全局路径规划在已知的环境中可以找到最优解，但当面对动态路径时，无法及时做出相应的校正，实时性较差.

在工业中应用最广泛的是模型预测控制（model predictive control，MPC）^[9-10]，该模型通用性强，能实时滚动优化，能够解决大规模约束问题的同时，具有良好的追踪性能和较强的抗干扰能力等特性. 借助预测控制的优势，文献 ^[11] 将贝叶斯神经网络和模型预测控制相结合，精确机械臂的模型同时保证机械臂作业过程中的安全性，通过分层的模型预测控制策略识别并利用不确定信息来预测下一时刻的状态; 文献 ^[12] 提出了一种新型自适应模糊模型预测控制器，该控制器可在水下环境中高效运行，并能大大减少计算负担. 针对机械臂在复杂环境下难以实现高精度运动跟踪的问题，文献 ^[13] 提出基于自适应动态规划与滑模导纳控制相结合的最优控制方法，并对价值函数中 R矩阵进行了优化改进，提升了跟踪精度. 对输入最大或最小时 PID 无法完整跟踪参考信号的问题，文献 ^[14] 将MPC与PID算法进行比较，证明在输入信号达到饱和时，MPC仍然具有完整且良好的信号跟踪能力. 即使MPC在工业界的应用已经非常广泛，但是对于大规模约束的复杂系统，模型求解以及迭代优化的问题，成为了当下凸优化问题研究中的难点. 针对凸优化求解的问题，文献 ^[15] 提出的误差求和增强牛顿法（error-summation enhanced Newton，ESEN）结合增强型Newton迭代法，使得约束条件不仅能满足系统本身的优化问题还能满足稳定性和收敛性的要求. 其中的积分项在应对常值干扰时，有不错的效果，但在面对动态系统中的扰动时，其抑制效果却难以保持.

针对上述问题，本文引入预测控制方法去规划路径以及优化轨迹，并且提出 MESEN（modified ESEN）算法，在原算法的基础上加入了重复控制项，能够更好的跟踪动态系统，减少滚动优化过程中对系统初始偏差的依赖性.

2 机械臂运动学模型

选取合适的坐标系是建立机械臂运动状态模型的关键步骤，本文所建立机械臂各关节坐标系如图1. 利用关节连杆之间的关系将关节1的坐标系映射到基坐标系，然后将关节2的坐标系映射到关节1再映射到基坐标系，将6个关节坐标系依次按照上述方式映射.

由上述关系坐标转换得到机械臂DH参数如表1.

结合DH参数表以及图1中机械臂关节的坐标转化关系，得到机械臂的齐次变换矩阵 ^[16]，得出机械臂正运动学方程为

\{\begin{matrix} T_{e}^{b} (q) = T_{6}^{0} = T_{0}^{1} T_{1}^{2} T_{2}^{3} T_{3}^{4} T_{4}^{5} T_{5}^{6} = \\ [\begin{matrix} x_{e}^{b} & y_{e}^{b} & z_{e}^{b} & p_{e}^{b} \\ 0 & 0 & 0 & 1 \end{matrix}], \\ q = {[\begin{matrix} q_{1} & q_{2} & q_{3} & q_{4} & q_{5} \end{matrix} q_{6}]}^{T}, \end{matrix}

(1)

其中: e为末端坐标系，b为基坐标系，q为机械臂各关节角度组成的向量.

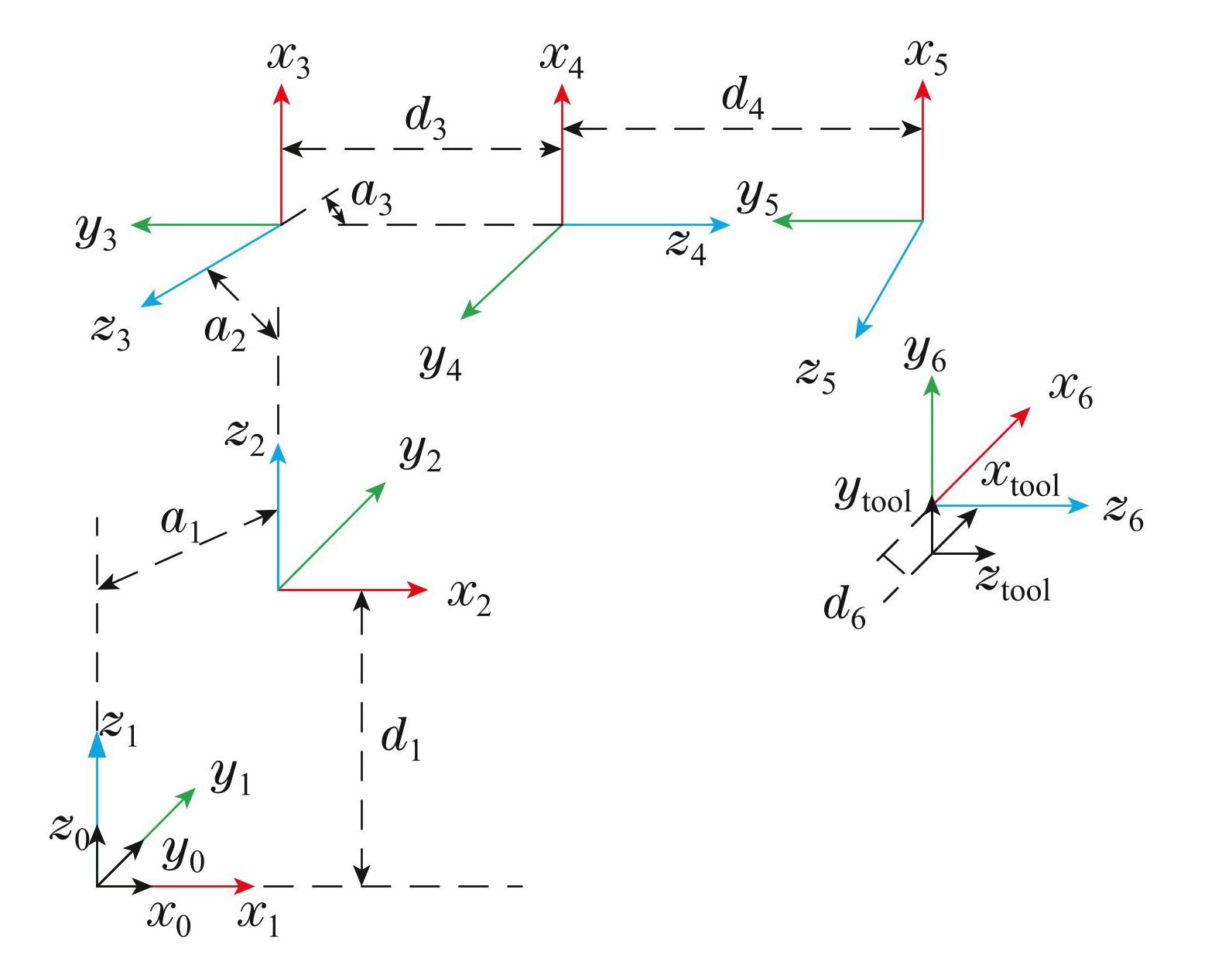
图1机械臂各关节坐标系

Fig.1The coordinate system of each joint of the robotic arm

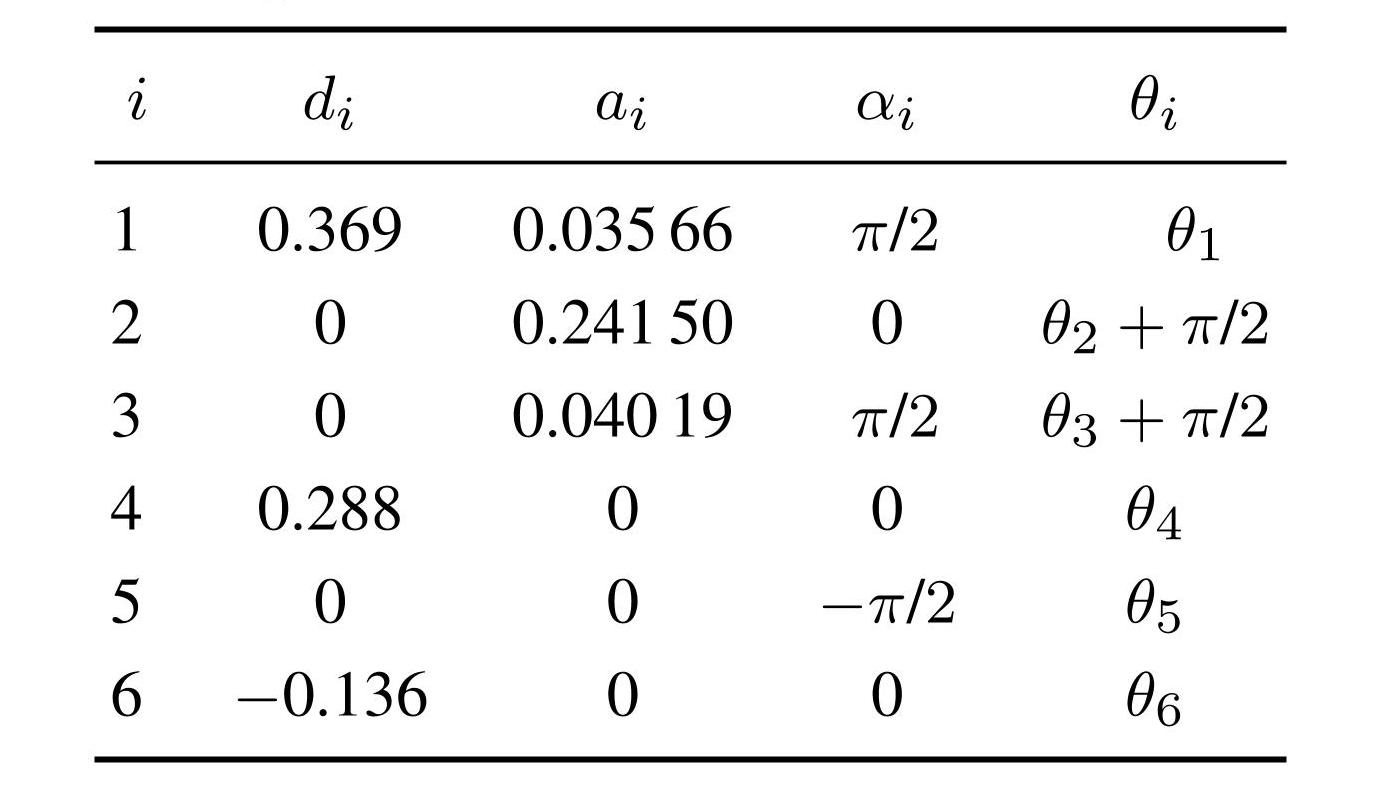
表1六轴机械臂DH参数表

Table1The DH parameter table of six-axis manipulators

经过计算，末端执行器的位置可以表示为

P_{e}^{b} = {[\begin{matrix} P_{11} P_{21} P_{31} \end{matrix}]}^{T},

(2)

其中P为机械臂末端位置，表示在一定关节角度下能够得到的唯一末端位置，包含X，Y，Z 3个方向.

常用求逆解方式是根据DH参数得到雅可比矩阵，由雅可比矩阵的伪逆矩阵 ^[17] 确定迭代方向，并通过迭代的方式使得关节角度收敛至目标位置.

由雅可比矩阵表示关节角度微分与末端位置微分的线性关系可以得到

d q = J (q)^{†} \cdot d x

(3)

其中: dx为机械臂末端广义关节速度的微分形式，dq 是空间的速度微分形式，J（q）^†是关于关节空间位置的雅可比矩阵的伪逆矩阵.

3 位置控制器的设计

根据图1中的基坐标得出机械臂末端的三维位置为r（x，y，z），六轴关节表示为q，关节速度为

\dot{q}

、关节加速度为

\ddot{q}

. 则机械臂末端在空间中的位置可以表示为

x = r (x, y, z)

(4)

其中x，y， z均为关节角q的函数，且满足x = f（q）.

将式（4）表示为标准的离散时间状态方程，设控制周期为τ，则在k + 1时刻上述描述可以表示为

x_{[k + 1 ∣ k]} = x_{[k ∣ k]} + τ {\dot{x}}_{[k ∣ k]} = x + τ \frac{\partial f (q)}{\partial q} \cdot \dot{q},

(5)

式中

\frac{\partial f （ q ）}{\partial q}

用B（q）表示，即雅可比矩阵，B（q）随着关节角度变化而变化，每次关节角度更新则B（q）也会发生变化，因此所构造的系统为时变系统.

在式（5）所表示的状态方程写成矩阵形式，并在离散化的基础上定义控制输入增量

Δ u_{[k ∣ k]} = u_{[k ∣ k]} - u_{[k ∣ k - 1]},

(6)

则机械臂末端位置状态方程为

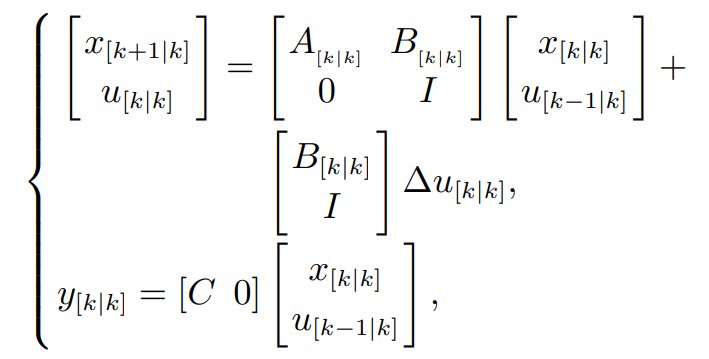
(7)

其中: A表示输入状态矩阵， B表示控制状态矩阵且该矩阵为雅可比矩阵; u表示输入关节角度导数，y为输出量.

根据式（6）定义，可得出增广状态向量为

{\tilde{x}}_{[k∣ k]} = {[\begin{matrix} x_{[k∣ k]} u_{[k - 1 ∣ k]} \end{matrix}]}^{T}

，联合式（7）可得该机械臂运动系统的预测模型为

\{\begin{matrix} X_{[k ∣ k]} = M {\tilde{x}}_{[k ∣ k]} + E Δ U_{[k ∣ k]}, \\ Y_{[k ∣ k]} = C X_{[k ∣ k]}, \end{matrix}

(8)

其中输入矩阵与控制矩阵以及状态矩阵、输出矩阵和输入矩阵可以分别表示为

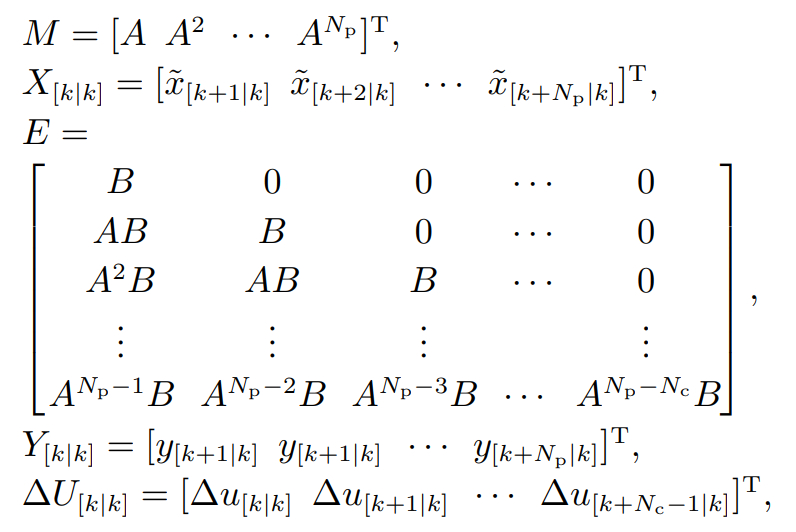
其中: 设预测长度为N_p，控制长度为N_c.

考虑在式（8）中加入关节角度约束、关节速度约束以及角加速度约束. 利用欧拉法并按照文献 ^[7] 将关节角度范围、关节速度范围以及关节加速度分别表示为离散时间下的形式，具体推导不再赘述，表示形式如式（9）–（10）所示.

关节速度约束表示为

[\begin{matrix} {\dot{q}}_{m i n} \\ {\dot{q}}_{m i n} \\ ⋮ \\ {\dot{q}}_{m i n} \end{matrix}] ⩽ [\begin{matrix} {\dot{q}}_{[k + 1 ∣ k]} \\ {\dot{q}}_{[k + 2 ∣ k]} \\ ⋮ \\ {\dot{q}}_{[k + N_{p} ∣ k]} \end{matrix}] ⩽ [\begin{matrix} {\dot{q}}_{m a x} \\ {\dot{q}}_{m a x} \\ ⋮ \\ {\dot{q}}_{m a x} \end{matrix}]

(9)

其中: q_min为各个关节最小旋转角度，q_max为各关节最大旋转角度.

同理，关节加速度可以表示为

[\begin{matrix} {\ddot{q}}_{m i n} \\ {\ddot{q}}_{m i n} \\ ⋮ \\ {\ddot{q}}_{m i n} \end{matrix}] ⩽ [\begin{matrix} {\ddot{q}}_{[k + 1 ∣ k]} \\ {\ddot{q}}_{[k + 2 ∣ k]} \\ ⋮ \\ {\ddot{q}}_{[k + N_{p} ∣ k]} \end{matrix}] ⩽ [\begin{matrix} {\ddot{q}}_{m a x} \\ {\ddot{q}}_{m a x} \\ ⋮ \\ {\ddot{q}}_{m a x} \end{matrix}]

(10)

结合式（8）–（10），得到含关节角度约束、关节速度约束以及关节加速度约束的机械臂预测控制器为

\begin{matrix} \underset{U_{k}}{m i n} J_{k} = \sum_{i = 0}^{N_{p} - 1} {‖C X_{k + i} - r_{k}‖}_{Q_{a}}^{2} + \sum_{i = 0}^{N_{c} - 1} {‖Δ U_{k + i}‖}_{R}^{2}, \\ s . t . \{\begin{matrix} Δ U_{k} = {[Δ u_{k} Δ u_{k + 1} \dots Δ u_{k + N_{c} - 1}]}^{T}, \\ U_{m i n} ⩽ U_{k} ⩽ U_{m a x}, \\ {|Δ U_{k}|}_{i} < Δ u_{m a x}, i = 1,2, \dots, N_{c}, \end{matrix} \end{matrix}

(11)

其中: r_k为机械臂的末端期望位置，Q_a = E^TQE为误差权重矩阵，R = diag{r}为控制加权矩阵，r为加权因子，引入输入增量控制∆U_k可以减小系统控制量波动.

4 基于MPC的MESEN在线求解

4.1 凸优化问题

针对前文所提的预测控制器，引入终端代价及终端约束，从而增大系统稳定性，并将其性能指标及约束重新描述为

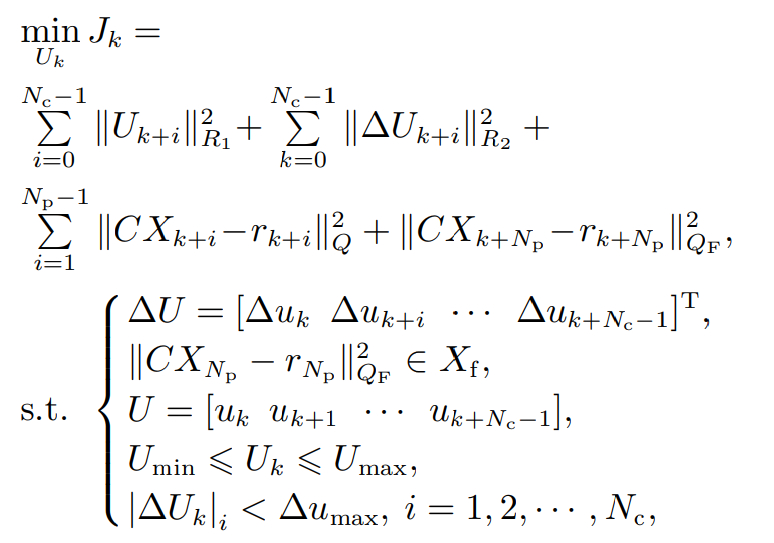
(12)

式中: Q和Q_F分别为非终端权重矩阵和终端权重矩阵，R₁和R₂分别为输入权重矩阵和输入增量权重矩阵，

{‖U_{k + i}‖}_{R_{1}}^{2}

项的引入体现了系统输入对系统的软约束，软约束可以使控制策略更加灵活并增强适应性，

{‖C X_{N_{p}} - r_{N_{p}}‖}_{Q_{F}}^{2}

代表终端约束属于终端约束集X_f .

为了解决式（12）所示的大规模求解问题，将式（12）转化为标准的二次规划型有

\begin{matrix} m i n \frac{1}{2} (Δ u)^{T} W (Δ u) + g^{T} (Δ u), \\ s . t . \{\begin{matrix} H_{1} (Δ u) ⩽ h_{1}, \\ H_{2} (Δ u) ⩽ h_{2}, \end{matrix} \end{matrix}

(13)

其中:

\begin{matrix} W = \\ 2 (S_{1}^{T} J_{1}^{T} Q J_{1} S_{1} + S_{2}^{T} J_{2}^{T} Q_{F} J_{2} S_{2} + E^{T} R_{1} E + R_{2}), \\ S_{1} = [\begin{matrix} τ & 0 & \dots & 0 \\ 2 τ & τ & \dots & 0 \\ ⋮ & ⋮ & ⋮ \\ N_{c} τ & (N_{c} - 1) τ & \dots & τ \\ (N_{c} + 1) τ & N_{c} τ & \dots & 2 τ \\ ⋮ & ⋮ & ⋮ \\ (N_{p} - 1) τ & (N_{p} - 2) τ & \dots & (N_{p} - N_{c}) τ \end{matrix}], \\ S_{2} = [\begin{matrix} N_{p} τ & (N_{p} - 1) τ & \dots & (N_{p} - N_{c} + 1) τ \end{matrix}], \end{matrix}

式中: J为前文所求得的雅克比矩阵，E为单位矩阵.

将式（13）转化为KKT条件，有

\{\begin{array}{l} W (Δ u)^{*} + g + H_{1}^{T} λ_{1} + H_{2}^{T} λ_{2} = 0, \\ λ_{1} ⩾ 0, h_{1} - H_{1} (Δ u)^{*} ⩾ 0, \\ λ_{2} ⩾ 0, h_{2} - H_{2} (Δ u)^{*} ⩾ 0, \\ λ_{1} \cdot (h_{1} - H_{1} (Δ u)^{*}) = 0, \\ λ_{2} \cdot (h_{2} - H_{2} (Δ u)^{*}) = 0, \end{array}

(14)

式中:

λ \in R^{n (2 N + 4 N_{μ})} ， （ Δ u ）^{*}

是当前时刻最优解.

将KKT条件转化为线性等式问题便于后续求解. 同时根据非线性互补问题 ^[18] 定义

κ_{1} = (1 - ξ_{1}) (h_{1} - {H_{1} v)}_{+} λ_{1 +} - ξ_{1} \sqrt{{(h_{1} - H_{1} v)}^{2} + λ_{1}^{2}} ， κ_{2} = (1 - ξ_{2}) (h_{2} - {H_{2} v)}_{+} λ_{2 +} - ξ_{2} \sqrt{{(h_{2} - H_{2} v)}^{2} + λ_{2}^{2}}

. 根据κ₁和κ₂以及非线性互补函数特性对式（14）进行构建，表示成线性函数为

K x_{k} - y_{k} = 0

(15)

分别构建x，y，K为

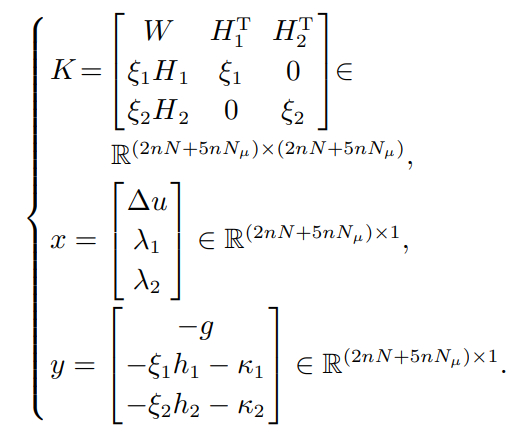
(16)

为了衡量计算精确度，定义误差函数形式如下:

e_{k} = K_{k} x_{k} - y_{k}

(17)

4.2 建立MESEN模型

将KKT函数根据牛顿迭代法的基本步骤，构造出一个向量值函数的牛顿法方程. 令e_k（t）=[e₁（t）e₂（t）· · ·

{e_{(2 n N + 5 n N_{μ})} （ t ）]}^{T}

，考虑其一阶逼近

e_{k} (t + z) \approx e (t) + ({\frac{\partial e (t)}{\partial t}|}_{t = t_{k}}) z .

(18)

将

\frac{\partial e （ t ）}{\partial t}

记为 J. 同时令一阶逼近为0向量，有J_kz = −e（t），使用广义逆得到 z = −

{(J_{k}^{T} J_{k})}^{- 1} J_{k}^{T} e （ t ）

，此时J为方阵且可逆，则得到牛顿迭代法的表达式为

x_{k + 1} = x_{k} - J_{k}^{- 1} e_{k},

(19)

其中: x_k为当前时刻所求解的根，x_k₊₁为最新的近似根，J是根据e_k求解得到的雅可比矩阵，由此构造出一个标准的牛顿迭代方程. 结合上述所建立线性函数，将J定义为

J = [\begin{matrix} W & H_{1}^{T} & H_{2}^{T} \\ L_{1} & L_{2} & 0 \\ L_{3} & 0 & L_{4} \end{matrix}]

(20)

式（21）中，ξ ∈（0，1），⊘表示Hadamard除法，使用 Hadamard变换能够有效处理矩阵中单个元素独立的问题，同时能够将数据归一化. Λ（·）表示对角矩阵，∂（·）∈[0，1]，∂（·）≥ 0. 此处，L₁，L₂，L₃，L₄分别表示为

(21)

由欧拉前向方程得到

{\dot{x}}_{k} (t) = \frac{x_{k + 1} (t) - x_{k} (t)}{τ},

(22)

其中τ >0且极小时满足上式描述，同时为了提高鲁棒性，在上述基础上增加重复控制项，形成的新数学模型如式（23）所示:

\begin{matrix} \dot{x} (t) = - J^{- 1} (\frac{1}{τ} e (t) + ς (- \frac{1}{2} + \int_{0}^{t} e (ω) d ω + \\ \int_{0}^{t} \frac{\cos ω}{ω} d ω)), \end{matrix}

(23)

式中ς >0，是重复控制项的权重系数，利用前向欧拉方程将上式进行离散化，其离散系统函数表达式为

\begin{matrix} x_{k + 1} = x_{k} - J^{- 1} (e_{k} + ς τ^{2} (- \frac{1}{2} + \\ \sum_{i = 0}^{k} e_{i} + \sum_{i = 0}^{k} s i n (ω_{i} k))), \end{matrix}

(24)

其中0 <ςτ² <1，ζ = ςτ². 经过以上的转换和推理，得到式（24）所示的MESEN算法模型. 该模型对线性函数重新构建得到新的模型，即在线性函数的基础上利用牛顿迭代法以及重复控制理论构造新的迭代模型.

4.3 MESEN算法收敛性分析

本文依据现有文献中的假设分析ESEN模型算法收敛性问题，然后通过引用相关的引理和定理来对算法进行收敛性分析. 将式（19）利用泰勒展开得到

e_{k + 1} = e_{k} + {\dot{e}}_{k} τ + \frac{{\ddot{e}}_{k}}{2} τ^{2} + O (τ^{2})

(25)

根据上一节所提出的MESEN算法将其线性化后可以得到上式，O（τ²）是包含重复控制中的二阶项的偏差向量，一般为无穷小量.

式（25）中二阶近似时，假设在无穷小区间

{\dot{e}}_{k}

是变化的，但

{\ddot{e}}_{k}

不变且近似为常值，则利用牛顿莱布尼茨公式以及极限定义有如下形式:

{\dot{e}}_{k} = \underset{τ \to 0}{l i m} \frac{e_{k + 1} - e_{k}}{τ},

(26)

由式（26）得到

\begin{matrix} x_{k + 1} - x_{k} = \\ - J^{- 1} (e_{k} + ς τ^{2} (- \frac{1}{2} + \sum_{i = 0}^{k} e_{i} + \sum_{i = 0}^{k} s i n (ω_{i} k))) . \end{matrix}

(27)

对式（27）利用极限定义有

\begin{matrix} J \cdot \underset{τ \to 0}{l i m} \frac{- (x_{k + 1} - x_{k})}{- τ} = \\ \underset{τ \to 0}{l i m} (e_{k} + ς τ^{2} (- \frac{1}{2} + \sum_{i = 0}^{k} e_{i} + \sum_{i = 0}^{k} s i n (ω_{i} k))) . \end{matrix}

(28)

将上式化简得到

J \cdot {\dot{x}}_{k} = {\dot{e}}_{k} = \underset{τ \to 0}{l i m} \frac{e_{k + 1} - e_{k}}{τ}

(29)

由此，得到

{\ddot{e}}_{k}

与新的模型之间的关系如下:

\begin{matrix} {\dot{e}}_{k} = J \cdot J^{- 1} (- \frac{1}{τ} (e_{k} + ς τ^{2} (- \frac{1}{2} + \\ \sum_{i = 0}^{k} e_{i} + \sum_{i = 0}^{k} s i n (ω_{i} k)))) . \end{matrix}

(30)

利用前向欧拉差分公式得到

e_{k + 1} - e_{k} = - (e_{k} + ζ (- \frac{1}{2} + \sum_{i = 0}^{k} e_{i} + \sum_{i = 0}^{k} s i n (ω_{i} k))) - τ O (τ),

(31)

其中: O（τ）无穷小为截止误差; 0 <ζ <1，ζ = ςτ²，右边第2项为该系统设计的重复控制的离散形式. 引入重复控制是为了在原来模型的基础上，进一步提高系统的控制效果，简化迭代过程. 经上述证明推导得到下式所示等式:

ζ (- \frac{1}{2} + \sum_{i = 0}^{k} e_{i} + \sum_{i = 0}^{k} s i n (ω_{i} k)) + e_{k + 1} + O (τ^{2}) = 0 .

(32)

在式（31）的基础上，利用李雅普诺夫分析上文所提模型的稳定性和收敛性，证明式（24）全局收敛于差值，首先构造出李雅普诺夫函数，令式（22）中

\dot{x} = f （ x ）

，

A （ x ） = \frac{\partial f}{\partial x}

，其中J >0且为雅可比矩阵，则有−J⁻¹ = A，同时在领域内满足A+A^T <0和Krosovskii Theorem理论，故构造李雅普诺夫函数为 ^[15]

V = (J x)^{T} (J x),

(33)

其中: V（0）= 0， V（Jx）= e >0，当 Mx ≠ 0，V >0，将上式结合式（29）的离散时间函数并依据李雅普诺夫定理有

Δ V (x_{k}) = V (x_{k + 1}) - V (x_{k}) .

(34)

结合式（31）得到

\begin{matrix} Δ V (x_{k}) = \\ {(- ζ (- \frac{1}{2} + \sum_{i = 0}^{k} e_{i} + \sum_{i = 0}^{k} s i n (ω_{i} k)))}^{T} \times \\ (- ζ (- \frac{1}{2} + \sum_{i = 0}^{k} e_{i} + \sum_{i = 0}^{k} s i n (ω_{i} k))) = \\ ζ^{2} (- \frac{1}{ζ} (e_{k}^{T} e_{k}) - \frac{1}{ζ} (e_{k}^{T} e_{k}) + e_{k}^{T} e_{k}) + O (τ^{2}) . \end{matrix}

(35)

显然，式（35）整体是小于零，即∆V <0，变化率为负. 总体而言，模型满足以下3个条件:

1）在e_k = 0时，V_k= 0;

2）在e_k ≠ 0时，V_k₊₁ >0;

3) ∆V <0.

满足李雅普诺夫定理，式（35）说明系统是渐进稳定的. 同时，重新整理后得到如式（36）所示形式:

l i m Δ V = \underset{k \to \infty}{l i m} (ζ^{2} {‖e_{k}‖}^{2} + O (τ^{2})),

(36)

其中当k → ∞时，式（36）仍然小于零且在某一时刻为恒定的值，李雅普诺夫定理说明该系统是稳定的且在全局范围内收敛，并且误差逐渐收敛于零.

5 实验结果与分析

根据上文建立的 DH参数表以及 Robotics Toolbox ^[19] 工具箱建立机械臂模型，得到MATLAB中机械臂模型如图2.

图2MATLAB中机械臂模型

Fig.2Model of a robotic arm in MATLAB

根据本文所研究机械臂实际位置，给定机械臂末端X轴、Y 轴和Z轴空间参考位置，机械臂末端位置控制的起始点为（0.324，0，0.515），时间步长 T = 0.1 s（k = 100），设置机械臂末端最终目标位置为（0.138，0.284，0.812）.

仿真中给定初始关节角度为 [−2.88 −1.570 8 2.094 2.094 0 1.05] rad，位置约束上限为 [0.441 0.489 1.035] m，位置约束下限为 [−0.383 −0.285 0.045] m. 关节角度约束上限为 [2.88 1.08 2.27 2.71 1.83 6.26] rad，关节角度约束下限为 [−2.88 −2.094 −1.05 −2.71 −2.71 −6.26] rad，关节正转最大速度约束为 [2.457 2.457 2.505 2.235 2.029 2.472] rad/s，关节反转最大速度约束为 [−2.457 −2.457 −2.505 −2.235 −2.029 −2.472] rad/s. 关节最大加速度为 [2.457 2.457 2.505 2.235 2.029 2.472] rad /s²，关节最大减速度为 [−2.457 −2.457 −2.505 −2.235 −2.029 −2.472] rad /s²，N_P = 20.

5.1 仿真对比

机械臂在无约束状态下，执行路径跟踪计算所需的步长较大，甚至会出现关节角度和位置超出实际机械臂出厂所设定范围的情况，这样操作对于机械臂关节的磨损非常严重，会损坏机械臂的关节控制器. 针对上述问题，考虑在优化函数中加入位置约束、关节角度约束以及关节角速度约束，并对终端位置X，Y，Z的权重进行调节，在调整输出权重后，控制效果显著改善，收敛更为迅速且稳定. 这种权重调整策略提升了整体系统的性能，确保了更好的输出稳定性. 此外，在调整权重后的函数模型中加入终端约束集Xf进行仿真对比实验，验证本文位置模型预测控制器的效果，3种模型的终端位置和关节角度阶跃响应输出曲线如图3–4所示.

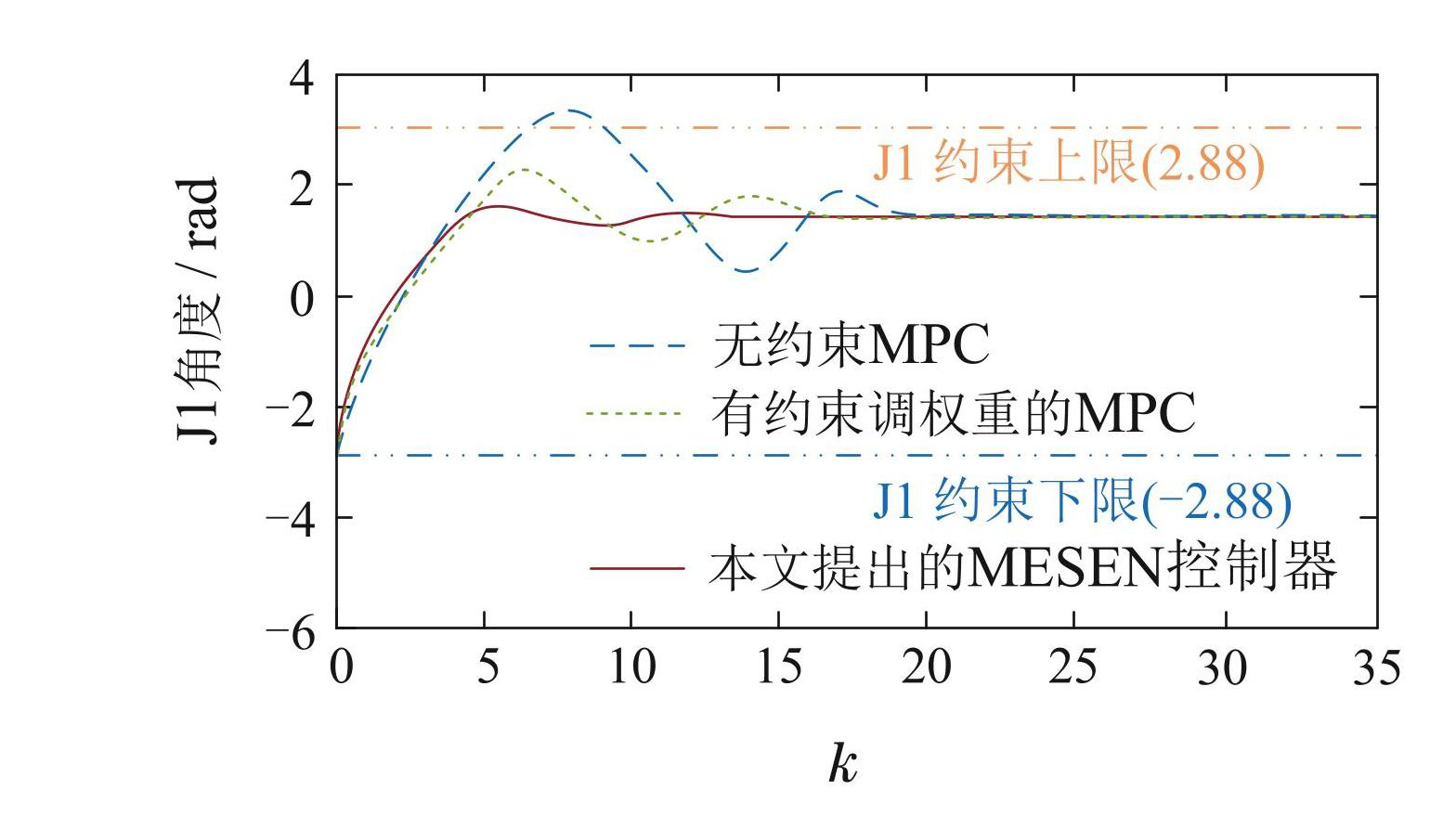
图33种控制器对应的终端位置

Fig.3Terminal positions corresponding to the three controllers

从仿真结果看，引入终端约束集的MESEN控制器则进一步提高了收敛速度和稳定性. 终端约束提供了对机械臂最终状态的明确限制，使得控制策略不仅在优化过程中更加稳健，系统还能有效地在安全范围内运行. 因此，含终端约束集的MESEN控制器能够更好地满足控制目标和系统安全性要求.

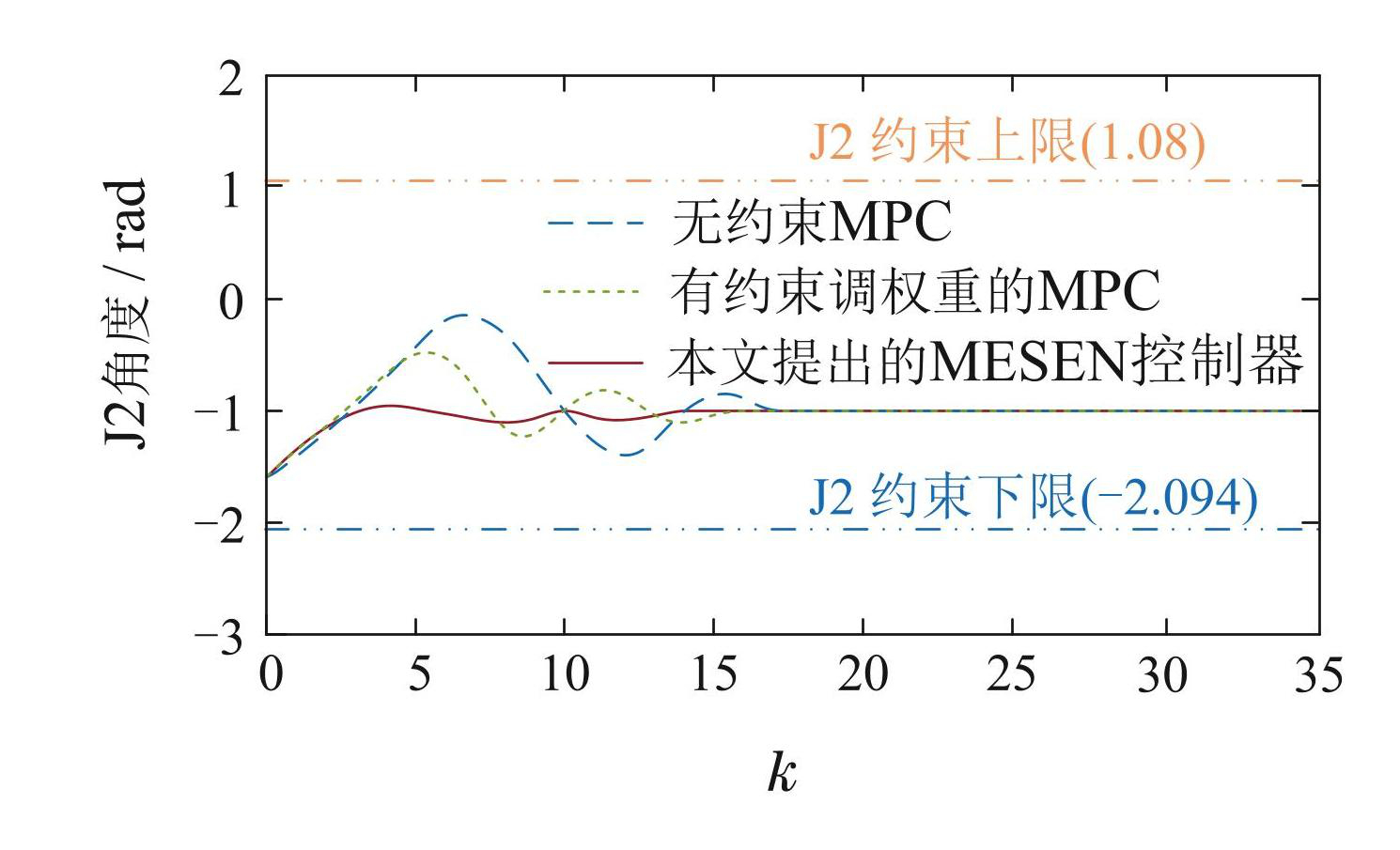
图43种控制器对应的关节角度

Fig.4Joint angles corresponding to the three controllers

5.2 物理平台实验

将MATLAB软件与图5所示机械臂联合建立实验环境，在含终端约束的基础上对所提的算法进行实验，选择对应的六自由度机械臂相应参数并给定系数矩阵，如表2所示.

按给定的初始值和在约束范围内设置的目标值，在无扰动和周期性扰动的情况下，利用所提MESEN 算法控制器和有约束MPC对机械臂进行轨迹跟踪，观察两种算法对所设目标运动轨迹的跟踪情况，分析所提MESEN算法跟踪效果.

图5机械臂和控制系统结构

Fig.5Robotic arm and control system structure

在无扰动状态下，机械臂在 MPC算法和 MESEN 算法控制下，系统输出如图6所示. 相比约束MPC，本文提出的MESEN控制器的跟踪误差更小，精度更高.

观察图7–8中两种模型预测控制算法对机械臂运动轨迹控制的输出曲线来看，MESEN算法控制轨迹的关节角度和关节角速度变化相较于MPC算法更平稳，具有更小的超调以及更好的稳定性.

在控制量上叠加一个周期正弦扰动，测试机械臂在MPC算法和MESEN算法控制下的跟踪效果. 观察图9–10中两种模型预测控制算法对机械臂运动轨迹控制的输出曲线，可以明显看出，在有扰动的情况下，MPC算法的输出出现振荡，并未能收敛到期望位置. 而采用MESEN算法控制的机械臂在受到干扰时，关节角度和关节角速度的变化能够迅速响应，并始终保持在关节约束范围内. 这表明，所提出的MESEN算法稍有振荡然后收敛，能够有效保障机械臂在操作过程中的安全运行，能够消除外部干扰的影响，确保轨迹跟踪的准确性和稳定性.

从实验结果来看，所提MESEN模型预测控制算法是有效的. 从跟踪效果以及关节角度、关节角速度等性能的变化趋势来看，MESEN控制策略的收敛速度快且能够快速稳定在一定范围内.

表2实验参数

Table2Experiment parameters

图6机械臂运动轨迹曲线

Fig.6Trajectory curve of the robotic arm

图7关节角度变化曲线

Fig.7Change of joint angle curves

图8关节角速度变化曲线

Fig.8Change of joint angular velocity curves

6 结论

本文首先根据六轴机械臂运动学原理设计了六轴机械臂路径跟踪控制器，在运动控制模型中增加了约束条件，并将一般模型转化为含有约束的标准模型. 然后通过调节各权重系数以及终端权重系数更新局部变量，进而更新全局变量，进行下一次迭代优化，使得整个系统处于稳定且能时刻更新的状态. 最后通过实验验证，该算法使多轴机械臂运动系统的收敛速度更快且提高了机械臂运动系统的精确性和稳定性. 本文所提算法提高了模型计算的效率，同时也提高了系统的稳定性和收敛性，但未能对动态环境下的干扰进行避障算法设计.

未来将在本文基础上对动态环境干扰下的避障算法进行探究.

图9关节角度变化曲线（周期干扰）

Fig.9Change of joint angle curves (periodic disturbances)

图10关节角速度变化曲线（周期干扰）

Fig.10Change of joint angular velocity curves (periodic disturbances)

图1机械臂各关节坐标系

Fig.1The coordinate system of each joint of the robotic arm

下载: 全尺寸图片

图2MATLAB中机械臂模型

Fig.2Model of a robotic arm in MATLAB

下载: 全尺寸图片

图33种控制器对应的终端位置

Fig.3Terminal positions corresponding to the three controllers

下载: 全尺寸图片

图43种控制器对应的关节角度

Fig.4Joint angles corresponding to the three controllers

下载: 全尺寸图片

图5机械臂和控制系统结构

Fig.5Robotic arm and control system structure

下载: 全尺寸图片

图6机械臂运动轨迹曲线

Fig.6Trajectory curve of the robotic arm

下载: 全尺寸图片

图7关节角度变化曲线

Fig.7Change of joint angle curves

下载: 全尺寸图片

图8关节角速度变化曲线

Fig.8Change of joint angular velocity curves

下载: 全尺寸图片

图9关节角度变化曲线（周期干扰）

Fig.9Change of joint angle curves (periodic disturbances)

下载: 全尺寸图片

图10关节角速度变化曲线（周期干扰）

Fig.10Change of joint angular velocity curves (periodic disturbances)

下载: 全尺寸图片

表1六轴机械臂DH参数表

Table1The DH parameter table of six-axis manipulators

下载: 全尺寸图片

表2实验参数

Table2Experiment parameters

下载: 全尺寸图片

图1机械臂各关节坐标系

Fig.1The coordinate system of each joint of the robotic arm

图2MATLAB中机械臂模型

Fig.2Model of a robotic arm in MATLAB

图33种控制器对应的终端位置

Fig.3Terminal positions corresponding to the three controllers

图43种控制器对应的关节角度

Fig.4Joint angles corresponding to the three controllers

图5机械臂和控制系统结构

Fig.5Robotic arm and control system structure

图6机械臂运动轨迹曲线

Fig.6Trajectory curve of the robotic arm

图7关节角度变化曲线

Fig.7Change of joint angle curves

图8关节角速度变化曲线

Fig.8Change of joint angular velocity curves

图9关节角度变化曲线（周期干扰）

Fig.9Change of joint angle curves (periodic disturbances)

图10关节角速度变化曲线（周期干扰）

Fig.10Change of joint angular velocity curves (periodic disturbances)

表1六轴机械臂DH参数表

Table1The DH parameter table of six-axis manipulators

表2实验参数

Table2Experiment parameters

图1机械臂各关节坐标系

Fig.1The coordinate system of each joint of the robotic arm

图2MATLAB中机械臂模型

Fig.2Model of a robotic arm in MATLAB

图33种控制器对应的终端位置

Fig.3Terminal positions corresponding to the three controllers

图43种控制器对应的关节角度

Fig.4Joint angles corresponding to the three controllers

图5机械臂和控制系统结构

Fig.5Robotic arm and control system structure

图6机械臂运动轨迹曲线

Fig.6Trajectory curve of the robotic arm

图7关节角度变化曲线

Fig.7Change of joint angle curves

图8关节角速度变化曲线

Fig.8Change of joint angular velocity curves

图9关节角度变化曲线（周期干扰）

Fig.9Change of joint angle curves (periodic disturbances)

图10关节角速度变化曲线（周期干扰）

Fig.10Change of joint angular velocity curves (periodic disturbances)

表1六轴机械臂DH参数表

Table1The DH parameter table of six-axis manipulators

表2实验参数

Table2Experiment parameters

LI Li, SHANG Junyun, FENG Yanli,et al. Research of trajectory planning for articulated industrial robots: A review. Computer Engineering and Applications,2018,54(5):36-50.(李黎, 尚俊云, 冯艳丽, 等. 关节型工业机器人轨迹规划研究综述. 计算机工程与应用,2018,54(5):36-50.)

GUO Jingjing, LIU Yungang, MAN Yongchao,et al. Autonomous multirotor UAV systems: Perception,planning and control. Control Theory & Applications,2024,41(10):1707-1725.(郭晶晶, 刘允刚, 满永超, 等. 自主多旋翼无人机系统: 感知、规划与控制. 控制理论与应用,2024,41(10):1707-1725.)

ZHANG X, MA J, HUANG S,et al. Integrated planning and control for collision-free trajectory generation in 3D environment with obstacles. The 19th International Conference on Control, Automation and Systems(ICCAS). Jeju, Korea: IEEE,2019:974-979.

FU X, QIAN D. Research on automatic trajectory planning method of unmanned ships based on multi-objective optimization. IEEE Access,2023,11:129829-129839.

LENG Shu, WU Ke, JU Hehua. Overview of manipulator kinematics modeling and solving method. Journal of Astronautics,2019,40(11):1262-1273.(冷舒, 吴克, 居鹤华. 机械臂运动学建模及解算方法综述. 宇航学报,2019,40(11):1262-1273.)

AL-HAMADANI A A, AL-FAIZ M Z. Design and implementation of inverse kinematics algorithm to manipulate 5-DOF humanoid robotic arm.2021 International Conference on Innovation and Intelligence for Informatics, Computing,and Technologies(3ICT). Zallaq, Bahrain: IEEE,2021:693-697.

PENG Xiang, XIANG Fenghong, MAO Jianlin. Mobile robot path planning method under multi-terrain constraints. Journal of Chinese Computer Systems,2021,42(9):1900-1905.(彭湘, 向凤红, 毛剑琳. 多地形约束条件下的移动机器人路径规划方法. 小型微型计算机系统,2021,42(9):1900-1905.)

WANG N, XU H. Dynamics-constrained global-local hybrid path planning of an autonomous surface vehicle. IEEE Transactions on Vehicular Technology,2020,69(7):6928-6942.

HE Shaoying, LI Dewei, XI Yugeng. Design of visual servo system for a 5DOF manipulator based on predictive control. Proceedings of 2017 Chinese Automation Congress(CAC2017)and China Intelligent Manufacturing Innovation Conference(CIMIC2017). Jinan, China: Chinese Automation Congress,2017:8.(何邵颖, 李德伟, 席裕庚. 基于预测控制的五自由度机械臂的视觉伺服系统设计.2017年中国自动化学会(CAC2017)暨国际智能制造创新大会(CIMIC2017)论文集, 山东, 济南,2017:8.)

LING L, HUANG S, CAO G,et al. Comparison analysis on controlincrement-based and control-quantity-based predictive controls of permanent magnet synchronous motors. IEEE International Conference on Predictive Control of Electrical Drives and Power Electronics(PRECEDE). Wuhan, China: IEEE,2023:1-6.

CURSI F, MODUGNO V, LANARI L,et al. Bayesian neural network modeling and hierarchical MPC for a tendon-driven surgical robot with uncertainty minimization. IEEE Robotics and Automation Letters,2021,6(2):2642-2649.

YANG Z, REN C. An adaptive fuzzy model predictive control method for underwater robotic arms. The 2023 42nd Chinese Control Conference(CCC). Tianjin, China: Chinese Automation Congress,2023:2723-2728.

LI Ming, XU Qun, WANG Yan,et al. Simulation and research of manipulator motion strategy based on adaptive dynamic programming. Journal of System Simulation,2023,35(10):2182-2192.(李明, 徐群, 王艳, 等. 基于自适应动态规划机械臂运动策略仿真研究. 系统仿真学报,2023,35(10):2182-2192.)

ARENA P, SUERI P, TAFFARA S,et al. MPC-based control strategy of a neuro-inspired quadruped robot. International Joint Conference on Neural Networks(IJCNN). Shenzhen, China: IEEE,2021:1-8.

ZHANG F, JIN L, LUO X. Error-summation enhanced newton algorithm for model predictive control of redundant manipulators. IEEE Transactions on Industrial Electronics,2023,70(3):2800-2811.

HUANG Guangwei, CHEN Junjie. Obstacle avoidance path planning of robotic arm and least-energy maneuver in a confined workspace. Modern Manufacturing Engineering,2024,1:39-44,109.(黄广伟, 陈军杰. 受限空间机械臂避障路径与能耗最优研究. 现代制造工程,2024,1:39-44,109.)

CAO Qixin, SUN Mingjing, XUE Wei,et al. Research on avoidance of dynamic obstacle and singularity for manipulator in human-robot cooperation. Journal Huazhong University of Science & Technology(Natural Science Edition),2020,48(1):55-59,65.(曹其新, 孙明镜, 薛蔚, 等. 人机协作下机械臂动态避障与避奇异研究. 华中科技大学学报(自然科学版),2020,48(1):55-59,65.)

CHEN B, CHEN X, KANZOW C. A penalized fischerburmeister NCP function. Mathematical Programming,2000,88:211-216.

CORKE P I. A robotics toolbox for MATLAB. IEEE Robotics & Automation Magazine,1996,3(1):24-32.