欢迎访问《控制理论与应用》期刊网站！

多维工艺信息融合的典型网状工艺路线自动化发现

doi: 10.7641/CTA.2024.40392

1. 安徽工程大学电气工程学院, 安徽芜湖 241000

2. 淮北师范大学计算机科学与技术学院, 安徽淮北 235000

3. 江南大学物联网工程学院, 江苏无锡 214122

基金项目: 国家自然科学基金项目(61973138), 安徽省高校自然科学研究项目(2023AH030081), 安徽省中青年教师培养行动项目(JNFX2023017), 芜湖市科技计划项目(2023jc05), 安徽工程大学国家自然科学基金预研项目(Xjky2022042), 检测技术与节能装置安徽省重点实验室开放基金项目(JCK20 22A09), 安徽省车载显示集成系统工程研究中心开放基金项目(VDIS2023B02)资助.

详细信息

作者简介

王梦娇硕士研究生,目前研究方向为智能工艺规划,E-mail: wmj20000525@163.com;

徐彬梓讲师,硕士生导师,目前研究方向为智能优化与调度理论方法,E-mail: xubinzi@ahpu.edu.cn;

黄登朝讲师,硕士生导师,目前研究方向为人工智能与无线传感器网络,E-mail: huangdengchao19@163.com;

王春讲师,硕士生导师,目前研究方向为智能优化与调度理论方法,E-mail: huaibeifwangchun@163.com;

王艳教授,博士生导师,目前研究方向为工业互联网系统优化控制,E-mail: wangyan88@jiangnan.edu.cn.

通信作者

徐彬梓，E-mail: xubinzi@ahpu.edu.cn.

Automated discovery of typical networked process routes with multi-dimensional process information fusion

WANG Meng-jiao¹ ， XU Bin-zi¹ ， HUANG Deng-chao¹ ， WANG Chun² ， WANG Yan³

1. School of Electrical Engineering, Anhui Polytechnic University, Wuhu Anhui 241000 , China

2. School of Computer Science and Technology, Huaibei Normal University, Huaibei Anhui 235000 , China

3. School of IOT and Engineering, Jiangnan University, Wuxi Jiangsu 214122 , China

Funds: Supported by the National Natural Science Foundation of China (61973138), the Natural Science Research Project of Anhui Educational Committee (2023AH030081), the Young and Middle-aged Teachers Training Action Project of Anhui Province (JNFX2023017), the Science and Technology Project of Wuhu (2023jc05), the Pre-research Project of the National Natural Science Foundation, Anhui Polytechnic University (Xjky20220 42), the Anhui Province Key Laboratory of Detection Technology and Energy-saving Devices Open Fund (JCK2022A09) and the Anhui Province Research Center for Vehicle-mounted Display Integration System Engineering Open Fund (VDIS2023B02).

摘要

大数据背景下, 典型工艺路线的有效发现可以为计算机辅助工艺规划(CAPP)的检索过程提供更加精准且充足的工艺信息, 从而提高后续工艺规划的质量. 但是现有与线性工艺路线相关的方法由于没有考虑网状工艺路线的结构复杂性, 既无法直接应用, 也难以合理量化其中的各类工艺信息. 此外, 大部分现有研究也忽略了典型工艺路线发现中的聚类有效性问题, 对这一问题缺乏合理的算法设计. 鉴于此, 本文提出了一种基于多维工艺信息融合的典型网状工艺路线自动化发现方法. 该方法针对网状工艺路线的相似度度量问题, 在信息需求分析的基础上, 为网状工艺路线中蕴含的4种工艺信息设计了不同的量化方法, 并通过主成分分析(PCA)将其合成综合相似度. 此外, 基于上述相似度度量的构建, 并考虑聚类有效性, 在传统近邻传播(OAP)算法中引入了火鹰优化算法(FHO), 以优化 AP算法的参考度与阻尼系数, 从而在聚类结果与软约束之间取得平衡, 以发现更符合实际需求的典型网状工艺路线. 仿真实验表明, 本文所提网状工艺路线的相似度度量能有效区分各种相似度情况, 具有更高的灵敏性. 同时, 引入的FHO能提高AP算法的聚类效果, 其中FHO-IAP相较于其他算法表现出更好的性能.

关键词

典型工艺路线 / 相似度度量 / 计算机辅助工艺规划 / 近邻传播算法 / 火鹰优化算法

Abstract

Under the big data era, the effective discovery of typical process routes can provide more accurate and sufficient process information for the retrieval process of computer aided process planning (CAPP), thus improving the quality of process planning. However, the existing approaches cannot be applied directly and are difficult to quantify the process information because they ignore the structural complexity of the networked process routes. In addition, most of the existing researches have overlooked the clustering effectiveness in the discovery of typical process routes, revealing a gap in effective algorithm design for this challenge. To address these shortcomings, this paper proposes an automated discovery method for typical networked process routes based on the multi-dimensional process information fusion. For the similarity measure, different quantification methods for the four types of process information are designed based on the information requirement analysis. Then, the proposed method integrates these findings into a comprehensive similarity using principal component analysis (PCA). Besides, considering the clustering effectiveness, the fire hawk optimizer (FHO) is introduced into the original affinity propagation (OAP) clustering algorithm to optimize its reference degree and damping coefficient, so that a balance between the clustering results and the soft constraints can be achieved. This way, typical networked process routes that are more in line with the practical requirements can be found. Simulation experiments validate that theproposed similarity measure for networked process routes can effectively distinguish various similarity cases with higher sensitivity. Meanwhile, the introduced FHO can enhance the clustering performance of AP, in which FHO-IAP shows the best clustering effect.

Keywords

typical process route / similarity measurement / CAPP / AP algorithm / FHO

1 引言 2 总体框架与研究思路 3 多维工艺信息融合的网状工艺路线相似度设计 3.1 网状工艺路线相似度设计的信息需求分析 3.1.1 先后顺序关系 3.1.2 工序间相似度 3.1.3 共同工序数 3.1.4 结构复杂度 3.2 网状工艺路线的不同相似情况 3.3 多维工艺信息融合的新型网状工艺路线综合相似度度量 3.3.1 工序间相似度度量 3.3.2 先后顺序关系度量 3.3.3 共同工序数计算 3.3.4 结构复杂度计算 3.3.5 多维工艺信息融合的新型网状工艺路线综合相似度 4 考虑聚类有效性的典型工艺路线发现 4.1 考虑聚类有效性的典型工艺路线发现问题 4.2 基于FHO优化AP的典型工艺路线发现方法 4.2.1 基于FHO-OAP的典型工艺路线发现方法 4.2.2 基于FHO-IAP的典型工艺路线发现方法 5 仿真实验验证 5.1 网状工艺路线综合相似度的性能分析 5.1.1 相似度性能指标 5.1.2 相似度度量性能比较 5.2 基于FHO优化AP的聚类方法性能分析 5.2.1 聚类性能指标 5.2.2 仿真实验设置 5.2.3 实验结果与性能分析 6 结语

1 引言

随着经济的不断发展，制造业迫切需要一种敏捷且有效的工艺规划方法来快速响应不断变化的市场需求 ^[1] . 作为产品设计与实际生产间的纽带，工艺路线的优劣直接决定了制造系统的生产质量与效率 ^[2] .

计算机辅助工艺规划（computer aided process planning，CAPP）是一种通过检索与推送典型工艺路线来辅助工艺规划的技术 ^[3] . 其所用典型工艺路线本质上是零件簇的工艺模板，它包含了簇中所有历史工艺路线中高度重合的共同工艺信息 ^[4] . 从集群的角度而言，典型工艺路线是零件簇的中心，它可以有效总结和代表同一簇中其他工艺路线的内在信息. 作为CAPP的基石，检索所得典型工艺路线的质量会直接影响后续工艺规划的效果 ^[5] .

在海量历史数据中发现典型工艺路线主要包含两部分: 相似度设计和聚类分析 ^[6] . 合理的相似度设计可以敏锐地量化工艺路线之间的共有信息，为后续的聚类分析提供细粒度的相似度度量，而聚类分析则是对海量工艺路线进行有效的归纳和总结，并将各聚类中心提取作为典型工艺路线 ^[7] . 在这过程中，若相似度设计或聚类效果不好，可能会生成不合理的典型工艺路线，也就无法有效指导后续的工艺规划过程 ^[8] .

目前有关研究大多数集中于线性工艺路线，忽视了网状工艺路线这一更符合实际且更加柔性的工艺表现形式 ^[9] . 不同于线性工艺路线，网状工艺路线具有易于系统重新配置和减少转换时间等优点，并且能够很好面对实际生产中遇到的各类突发状况 ^[10] . 因此，研究典型网状工艺路线的自动化发现问题更符合当前柔性化、智能化生产的迫切需求 ^[11] .

作为典型工艺路线发现的基础，线性工艺路线的相似度已经有大量前期研究. Choobineh ^[12] 最先研究了工序间的先后顺序关系，在他的研究中倡导使用邻近度量来形成零件簇. Zhou等人 ^[13] 考虑了零件的加工特征和拓扑关系中的工艺信息，并通过建立工艺路线的模糊相似性度量来发现典型工艺路线. Liu 等人 ^[14] 考虑了不同工序之间的相似度，引入了通过工序编码计算相似度的方案. 但是这些研究都忽略了工序相似度和先后顺序关系的相关性，只使用线性加权和来得到最终的结果. Xu等人 ^[15] 分析了典型工艺路线知识发现所需的必要工序信息，并以此提出了一种新的线性工艺路线综合相似度度量方法.

尽管线性工艺路线已经被深入研究，但这些为线性工艺路线设计的相似度度量不能直接用于网状工艺路线，因为网状工艺路线内部结构更为复杂且灵活，需要考虑的工艺信息更多. 此外，生产过程中的多种工艺信息与网状工艺路线的复杂结构相互耦合，想要有效度量这些工艺信息就显得更加困难.

Navaei等人 ^[16] 最先研究了网状工艺路线的相似度度量问题，该研究设计了一种新的相似度系数，在这其中考虑了先后顺序关系、共同工序数和体积相似性，并通过线性加权进行组合. 但是，所提方法将所有工序都看成完全不同的情况，忽视了工序间本身存在的相似关系.

设计好工艺路线的相似度度量后，对其进行聚类分析是发现典型工艺路线的第2步. 典型工艺路线发现的目的是通过历史工艺路线的有效聚类，从每个零件簇中挖掘和发现最具共性和代表性的工艺路线，并将其视为典型工艺路线. 因此，相较于传统聚类问题是将数据归类而言，典型工艺路线的发现问题是找出各聚类簇中包含最多共性工艺信息的真实工艺路线.

目前为止，国内外对于工艺路线的聚类问题已有了深入的研究. Wu等人 ^[17] 提出一种新的两阶段聚类方法，在第1阶段中，基于工序间相似性等准则对聚类簇进行识别; 在第2阶段中，将聚类簇合理分配到不同机器上，使总成本最小化. 王琳等人 ^[18] 通过近邻传播（affinity propagation，AP）算法对工艺过程进行聚类分析，并根据相关指标对聚类结果进行评价分析，得到有效聚类结果和最佳聚类数目. Li ^[6] 提出了一种基于多级信息熵的工艺路线相似度计算方法. 在此基础上，Li还提出了一种基于谱聚类和粒子群优化K-means算法的工艺路线聚类模型，根据所得相似度实现了对工艺路线的有效聚类.

然而，上述研究都忽视了典型工艺路线发现问题中聚类的有效性问题. Wang等人 ^[19] 最先在典型工艺路线发现问题中引入了数量约束和半径约束，来提高聚类结果的有效性和优化聚类数目. 但将这两个约束作为硬约束处理，这可能导致聚类结果不够灵活，无法很好地适应不同数据集的分布变化. 相比之下，徐彬梓 ^[20] 通过在传统AP算法（original AP，OAP）中加入半径软约束和数量软约束，设计出了改进的 AP 算法（improved AP，IAP）将约束参数的敏感度降低，从而提升聚类结果算法的有效性. 然而，徐彬梓的工作也存在问题. 引入了半径软约束和数量软约束的典型工艺路线发现问题相较于传统问题更加复杂，需要在聚类结果和软约束罚值间寻求平衡，而单靠人为设置合理的参考度（p）与阻尼系数（λ）显然非常困难，极易使IAP算法陷入局部最优，难以保证所得结果的全局最优性. 因此，如何寻找合适的参考度和阻尼系数是运用AP算法求解相关问题的关键之一.

为了有效解决上述问题，本文提出一种多维工艺信息融合的典型网状工艺路线自动化发现方法，其中的主要工作和创新点如下:

1）本文详细分析了计算网状工艺路线相似度时，需要考虑的工艺信息需求，并基于此构建了面向网状工艺路线的不同相似度情况案例库;

2）本文设计了一种面向网状工艺路线的新型综合相似度度量方法. 该方法创新性地将网状工艺路线中的先后顺序关系和工序相似度信息量化问题转化为工序对的加权二分图最大匹配问题，并通过库恩–曼克尔斯（Kuhn Munkres，KM）算法 ^[21] 对其进行了求解. 此外，所提方法还以Jaccard相似度 ^[22] 量化了共同工序数，以可选工艺路线数目量化了结构复杂度，并通过主成分分析（principal component analysis，PCA）整合成最终的综合相似度;

3）由于考虑了聚类有效性的典型工艺路线发现问题的求解难度陡增，为了解决AP算法输入参数难以人为调节的问题，本文将火鹰优化算法（fire hawk optimizer，FHO）^[23] 引入到了 AP 算法中，并提出了 FHOOAP和FHO-IAP两种算法变体，以实现对参考度（p）与阻尼系数（λ）的自动调整.

2 总体框架与研究思路

总体而言，本文所提“多维工艺信息融合的典型网状工艺路线自动化发现方法”主要解决两个问题:

1）为网状工艺路线设计细粒度的相似度度量;

2）在考虑聚类有效性的同时，提高典型网状工艺路线发现过程的聚类效果.

针对这两个问题，本文分别提出了多维工艺信息融合的网状工艺路线综合相似度度量（见第3节）和基于FHO优化AP的典型工艺路线发现方法（见第4节）. 这两者的联系在于，基于所提相似度度量计算得到的网状工艺路线相似度矩阵是FHO优化AP的聚类算法的输入，即聚类过程的数据基础.

3 多维工艺信息融合的网状工艺路线相似度设计

3.1 网状工艺路线相似度设计的信息需求分析

在设计网状工艺路线的相似度之前，需要先详尽分析网状工艺路线中包含了怎样的信息. 基于已有研究 ^[10，16]，本文结合生产过程的实际需求，认为网状工艺路线中存在4种工艺信息: 先后顺序关系、工序间相似度、共同工序数和结构复杂度，如图1所示. 这些信息尽可能地决定了一条工艺路线的唯一性，也能通过这些信息来度量不同工艺路线的相似性或差异性. 因此，深入分析和量化这些多维工艺信息，可以更合理且有效地设计网状工艺路线的相似度度量.

图1网状工艺路线的信息需求分析

Fig.1Information requirement analysis of the networked process routes

3.1.1 先后顺序关系

工艺路线中工序的先后顺序关系反映了工序间的依赖和约束关系，确保零件生产过程中工艺上的合理性. 相关研究已表明 ^[24]，同类型产品通常具有相似的工序先后顺序关系，因为它们的工艺需求大体相同.

在已有文献 ^[25] 中，先后顺序关系通常通过最长公共子串或最长公共子序列来衡量. 然而，这两种方法仅适用于线性工艺路线，因为网状工艺路线中存在多个可选路线，其结构更加复杂和灵活. 因此，在网状工艺路线中使用这些方法时，可能会造成部分公共子串或子序列的重复计算，从而影响相似度度量的准确性. 此外，相似度度量时还应考虑工序间的相似性，否则先后顺序关系将仅限于共同工序，忽略相似工序间的先后顺序信息. 因此，本文采用网状工艺路线的双结构矩阵和KM算法 ^[21] 来寻找最大权重匹配，从而同时衡量工序相似度和工序的先后顺序信息.

3.1.2 工序间相似度

工序作为工艺路线的最小单位，本身包含了大量的工艺信息. 在以往的研究中，只考虑了工序完全相同和完全不同两种情况，忽略了工序中嵌入的工艺信息. 遵循Liu等人 ^[14] 的研究基于国家标准使用三级代码来描述每个工序中与流程相关的信息，如图1所示.

3.1.3 共同工序数

在基于双结构矩阵和KM算法度量工序相似度和先后顺序关系的过程中，实际已经包含了共同工序的信息，因为共同工序本质上就是工序间相似度为1的工序对. 但上述度量方法不仅考虑了共同工序信息，也同时考虑了这些工序的先后顺序信息. 换言之，如果相同工序的顺序不同，那么上述方法则认为他们的相似度为0. 为了获取共同工序的独立信息，就需要将这部分信息与工序的先后顺序信息解绑. 为此，本文采用Jaccard相似度 ^[22] 来衡量共同工序之间的关联性.

3.1.4 结构复杂度

网状工艺路线的结构复杂度是评价其结构信息的重要指标之一，它反映了网状工艺路线中可选工艺路线的数量，即工艺路线的多样性和柔性. 在本文中，采用可选工艺路线的数量来衡量网状工艺路线的结构复杂度. 如此，线性工艺路线的结构复杂度即为1.

3.2 网状工艺路线的不同相似情况

在分析完网状工艺路线相似度设计的信息需求后，本节综合上述分析结果，总结出网状工艺路线的不同相似情况. 如表1所示，本文从工序、结构、顺序3个方面入手，考虑每个方面的可能情况，构建了一个面向网状工艺路线的相似情况案例库. 其中，图1所示的共同工序信息被认为是工序相似度为1的特殊情况. 这些不同的相似情况表明两条网状工艺路线间包含着不同的公共信息，从而导致不同的相似程度.

表13种不同相似情况

Table1Three different similar situations

根据表1，以原始工艺路线（记为OG）为基准，对其进行不同情况下的适当修改，可以建立39种不同的相似度情况，如图2所示. 一目了然，案例1的相似性最高，而案例38和39最差，此外，由于案例 37，38，39 与原始工艺路线OG没有任何共同或相似的工序，因此讨论这3个案例的先后顺序信息是没有意义的.

3.3 多维工艺信息融合的新型网状工艺路线综合相似度度量

本节提出一种面向网状工艺路线的新型综合相似度度量，通过对多维工艺信息的合理量化与融合，来保证相似度度量的有效性，其总体框架如图3所示.

3.3.1 工序间相似度度量

结合Liu等人 ^[14] 的研究，基于国家标准将工序表示为三位编码的形式. 接着，根据不同层级的工艺信息，通过同或运算（exclusive not or，XNOR）计算工序间相似度，

s_{o} (o_{x}, o_{y}) = \frac{\sum_{z = 1}^{3} o_{x}^{z} ⊙ o_{y}^{z}}{3},

(1)

其中

o_{x}^{z}

和

o_{y}^{z}

是两个工序的前z位编码.

3.3.2 先后顺序关系度量

由于工序之间具有不同的相似度（见式（1）），因此度量先后顺序关系显然不能忽略工序间的相似性. 如图3所示，本文采用双结构矩阵和KM算法 ^[26] 相结合的方式，将这两种工艺信息综合考虑和度量.

在此基础上，本节定义两个相邻工序对（分别记为 opr_i =（o_i₁，o_i₂）和opr_j =（o_j₁，o_j₂））的相似度为

s_{p r} ({o p r}_{i}, {o p r}_{j}) = \sum_{k = 1,2} 0.5 \times s_{o} (o_{i k}, o_{j k}),

(2)

其中s_o =（o_ik，o_jk）指工序o_ik与o_jk之间的相似度.

得到双结构矩阵之后，就可将先后顺序关系和工序间相似度的量化问题转化为加权二分图的最大匹配问题. 其中，双结构矩阵中的各相邻工序对就是相应的匹配对象，而匹配权重由式（2）计算得到. 如图4所示，采用KM算法 ^[26] 来求解双结构矩阵的最大匹配权重问题，并将得到的最大匹配权重作为相似度sW，即

s_{W} ({n o s}_{m}, {n o s}_{n}) = \frac{\sum s_{p r} ({o p r}_{i}, {o p r}_{j})}{m a x \{|{d s m}_{m}|, |{d s m}_{n}|\}},

(3)

在式（3）中，nos_m 和 nos_n为两条网状工艺路线，而 |dsm_m|和|dsm_n|是nos_m和nos_n对应双结构矩阵中相邻工序对的个数.

3.3.3 共同工序数计算

在实际中，仍然存在两条网状工艺路线虽然具有共同工序，但这些工序的顺序并不同的情况. 在这种情况下，共同工序的信息将被式（3）所忽略. 为此，本文引入Jaccard相似系数^[22]，以便独立度量两条网状工艺路线中共同工序的数量.

3.3.4 结构复杂度计算

工艺路线的长度和结构是比较不同工艺路线形状特征的重要指标. 长度是指工艺路线中包含的工序数量，可通过构建双结构矩阵来量化. 结构则描述了工艺路线的组织方式和复杂程度. 本文将网状工艺路线中可选择的工艺路线条数定义为结构复杂度. 由此，可以计算两条网状工艺路线结构复杂度的相似程度为

\begin{matrix} s_{S} ({m o s}_{m}, {m o s}_{m}) = \\ 1 - \frac{Δ_{p r}}{m a x \{|{m o s}_{m}|, |{m o s}_{n}|\}}, \end{matrix}

(4)

在式（4）中: ∆_pr是两条网状工艺路线的可选工艺路线数之差，|mos_m|和|mos_n|则是nos_m和nos_n这两条网状工艺路线的可选工艺路线数.

3.3.5 多维工艺信息融合的新型网状工艺路线综合相似度

如前文所述，网状工艺路线中的有效工艺信息包含4类，而本文通过3种中间相似度对其进行了量化. 在之前的研究中，大多数采用加权求和的方式得到综合相似度，而往往忽略了这些中间相似度之间的相关性和内在信息的重复性.

图2网状工艺路线的不同相似情况

Fig.2Different similar cases of the networked process routes

图3所需信息和相似度度量之间的层次关系

Fig.3The hierarchical relationship between the required information and the similarity measures

图4双结构矩阵

Fig.4Dual structure matrix

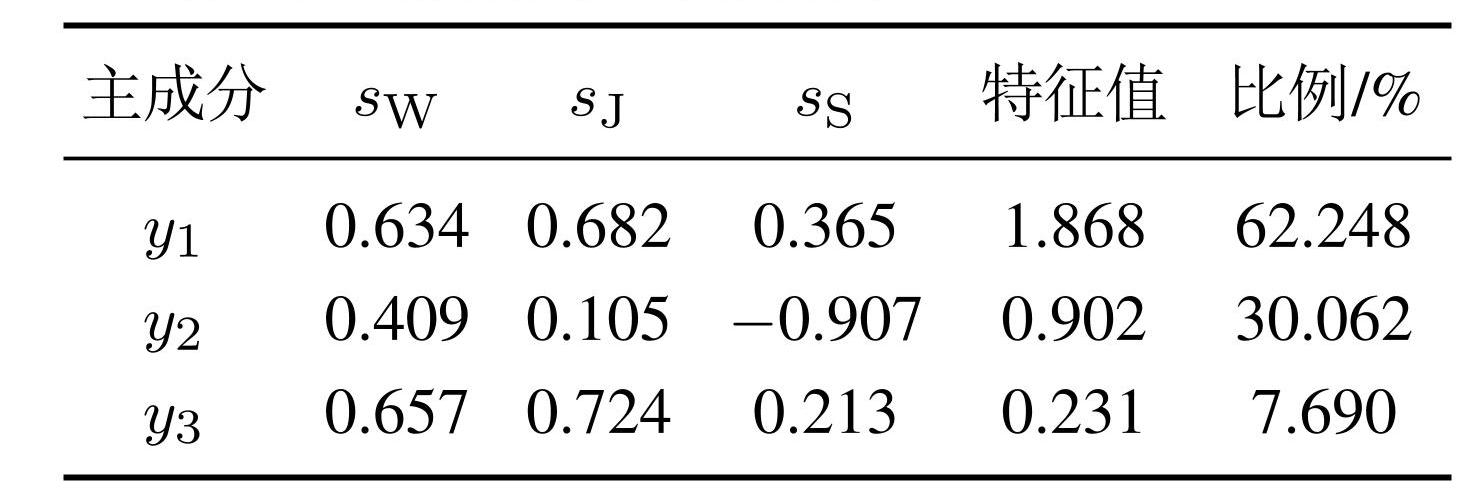
为了更直观地解释与分析3种中间相似度之间的相关性，本节以图2中构建的40条网状工艺路线为例计算了3种中间相似度彼此间的相关系数，计算所得结果分别如下: corr（s_J，s_W）= 0.736 4，corr（s_J，s_S）= 0.129 5 和corr（s_W，s_S）= 0.343 5. 这表明3种度量彼此之间都存在着一定的关联性，因此并不适合采用加权和. 故本文采用PCA方法来获得综合相似度，主成分分析的结果如表2所示. 根据表2的结果，本文选择 y₁ 和y₂ 来计算最后的综合相似度值.

表23个中间相似度的主成分分析结果

Table2Principal component analysis results of three intermediate similarities

4 考虑聚类有效性的典型工艺路线发现

4.1 考虑聚类有效性的典型工艺路线发现问题

典型工艺路线发现问题的核心在于通过聚类找到中心点，虽然线性工艺路线的相似度度量不能直接用于网状工艺路线，但聚类方法是相通的. 由于典型工艺路线聚类是一个实际问题，所以需要考虑聚类的有效性，具体而言，其中包括数量约束和半径约束 ^[20] .

数量约束是指每个聚类簇中的工艺路线数目应当超过最小数目n，而半径约束则是指每个聚类簇的半径应当小于最大的聚类簇半径ε. 前者用于保证聚类簇中包含有足够多的工艺数据，否则这一聚类簇中生成的典型工艺路径就不具有较高的普适性. 而后者则是用来保证发现的典型工艺路线，不会因为聚类簇中的工艺信息过多而难以很好的代表簇中的其他工艺路线. 这两个约束条件提出了聚类有效性的概念，从而使得发现的典型工艺路线更符合实际需求.

该问题的数学描述如下: 对于一个含有N条网状工艺路线的集合 X = {x₁，x₂，· · ·，x_N}，定义S = {sim（x_i，x_j）}为X中所有网状工艺路线之间的相似度集，其中sim（x_i，x_j）是由第3.3节提出的新型综合相似度计算得到. 定义q_e≥ 0和q_r ≥ 0分别是数量软约束和半径软约束的罚值，那么聚类算法的目标是找到中心集合O = {o₁，· · ·，o_K}使得目标函数最大化

\begin{matrix} n e t s i m = \sum_{i = {1,2, \dots, N}} s (x_{i}, O_{x i}) - q_{e} |X_{e}| - \\ (\sum_{x_{i} \in X_{r}} (\frac{ε - s (x_{i}, O_{x i})}{ε}) q_{r}), \end{matrix}

(5)

其中: O_xi为第i条工艺路线的中心，X_e和X_r分别是违反数量约束和半径约束的工艺路线集合，而ε是有效聚类簇的最大半径.

4.2 基于FHO优化AP的典型工艺路线发现方法

4.2.1 基于FHO-OAP的典型工艺路线发现方法

所提FHO-OAP算法相较于OAP算法有两个改进: 一是采用了FHO算法自动调优p与λ; 二是由于OAP 算法在聚类过程中并没有考虑数量软约束和半径软约束，故在OAP算法对网状工艺路线数据集进行聚类得到聚类结果之后，需要再根据式（5）计算数量软约束与半径软约束的罚值，并进行累加得到最终结果（即式（5）中的netsim），并视为FHO中个体的适应度值. netsim越大，表示对应聚类结果的效果越好. FHO-OAP具体流程如图5左边所示.

4.2.2 基于FHO-IAP的典型工艺路线发现方法

不同于OAP在聚类中并不考虑两个软约束，徐彬梓 ^[20] 所提IAP将两个软约束直接引入到AP算法的聚类过程中，因此IAP需要迭代更新4种信息变量. 这样的优势是IAP在聚类时不仅会考虑工艺路线间的相似度，还会考虑两个软约束的需求，从而得到一个使netsim尽可能大的折中结果. 但这样的劣势是，IAP所得结果的质量更加依赖于算法的参数. 因此，在本节中，同样将FHO用于优化IAP，如图5右边所示.

图5FHO-AP算法流程图

Fig.5Flow chart of the FHO-AP algorithm

5 仿真实验验证

5.1 网状工艺路线综合相似度的性能分析

5.1.1 相似度性能指标

采用图2所示的不同相似度情况作为本节的测试集P. 基于文献 ^[15] 的研究，本节采用的性能指标为

\begin{matrix} R (P, s i m) = \\ \frac{|\{({n o s}_{m}, {n o s}_{n}) ∣ r_{s i m} ({n o s}_{m}, {n o s}_{n}) = r_{r} ({n o s}_{m}, {n o s}_{n})\}|}{|\{({n o s}_{m}, {n o s}_{n} ∣ m, n \in [1, N])\}|}, \end{matrix}

(6)

其中: sim是给定的相似度度量， N是P中工艺路线的条数，而r_sim（nos_m，nos_n）是两条工艺路线的相似度， r_r（nos_m，nos_n）是这两条工艺路线的真实相似度. 若 r_sim（nos_m，nos_n）=r_r（nos_m，nos_n），则表明通过相似度度量sim计算所得的相似度与实际情况相符.

5.1.2 相似度度量性能比较

将本文所提方法与文献 ^[16] 和文献 ^[10] 中的相似度度量进行比较，其结果如图6所示. 总的来说，文献 ^[10，16] 所提方法的性能指标都为0.487，而本文所提相似度度量方法的性能指标为0.923. 这表明对于图2所示的39种不同的相似度情况，本文所提方法能有效区分更多的不同情况，从而为其赋予更加合理和细粒度的相似度值. 这一结果验证了本文所提方法在网状工艺路线相似度度量方面的优越性.

图6网状工艺路线相似度度量计算结果比较

Fig.6Calculation result comparisons of the similarity measures for the networked process route

具体而言，图6（a）表明文献 ^[16] 所提方法不能有效地度量工序间相似度与结构复杂性，所以OG与案例 10，11，12，13，14，15的相似度均为0.2. 而文献 ^[10] 对其的改进依旧没有考虑工序之间的相似度信息，所以它与文献 ^[16] 的计算结果相近.

本文所设计的相似度度量方法无法区分的相似情况是{17，18}，{20，21}和{23，24}. 图2已表明这些相似情况之间的唯一区别是顺序方面: a）顺序不同; b）部分顺序不同. 尽管案例18，21和24的工序顺序部分不同，但是本文提出的相似度度量方法无法找到这种相同的先后顺序关系. 这是因为本文所建立的双结构矩阵要求两个相邻工序之间有严格的连续关系，因而无法反映间隔工序之间的先后顺序关系.

5.2 基于FHO优化AP的聚类方法性能分析

本节采用图2所示40条网状工艺路线的数据集来验证所提算法的性能，并将其与已有的OAP算法 ^[27]、平均链接聚类（average linkage clustering，ALC）算法 ^[16，28]、IAP算法 ^[20] 以及改进后的K-medoids（improved K-medoids，IKM）算法 ^[15] 进行对比分析.

5.2.1 聚类性能指标

与传统聚类问题不同，本文研究的典型网状工艺路线发现问题旨在通过聚类过程从工艺路线数据集中筛选出最具代表性的典型工艺路线. 为了合理评估聚类结果的有效性，本文选择式（5）所示的netsim 作为本节的性能指标，该指标本质上是各工艺路线与其对应中心的相似度值以及两个软约束罚值的累加.

5.2.2 仿真实验设置

本节中对于仿真实验参数设置如下:

\begin{matrix} n = r o u n d (\frac{N}{K}), ε = m i n \frac{s (x_{i}, x_{j})}{K}, \\ q_{e} = 0.5, q_{r} = 1, \end{matrix}

其中: n表示数量软约束下有效聚类簇中工艺路线的最小数量; ε为半径软约束下有效聚类簇的最大半径; q_e和q_r分别是数量软约束和半径软约束的罚值; K表示不同情景下网状工艺路线数据集的理想聚类个数.

在本节实验中，主要是通过理想聚类个数K来设置不同的数量软约束n和半径软约束ε，以模拟不同情景下的典型工艺路线发现问题. 此处，q_e和q_r是根据相似度范围和两个软约束的罚值来设计的. 设置K的取值范围为1到8，以表示8个不同情景下的典型工艺路线发现问题. 在每次确定K的数值之后，各个算法重复运行5次并取均值和方差来衡量算法的真实性能.

5.2.3 实验结果与性能分析

表3给出了6种算法在该数据集上运行所得结果的均值与方差. 其中，加粗字体表示了相同问题配置下各算法所得的最优结果. 同时，基于 Friedman检验 ^[29] 计算了各算法的平均排名（Rank）.

从表3可知，本文所提FHO-IAP和FHO-OAP的聚类效果要明显好于已有的其他4种聚类算法. 这是因为所提算法不仅在聚类过程中就考虑了数量软约束和半径软约束，且通过FHO算法有效地优化了OAP算法和IAP算法中的p和λ，提高了原始算法的整体性能.

表340条网状工艺路线数据集的聚类结果与方差

Table3Clustering results and variance of 40 networked process route data set

此外，由OAP算法和FHO-OAP算法可知，它们的聚类效果差距不大; 但FHO-IAP算法的聚类效果明显优于IAP算法. 这是因为OAP算法本身更新传递的中间信息较少，计算过程相对简单，所以即使加入FHO 算法，其聚类效果的提升也小. 而IAP算法的聚类过程需要从聚类结果和软约束罚值中寻找平衡，所以更新的中间信息较多，问题更复杂. 在这种情况下，加入 FHO算法之后，其聚类效果提升更为明显.

比较所提方法可以发现FHO-IAP算法的效果更好. 这是因为FHO-IAP算法是将两个软约束加入到了聚类过程中，保证了FHO-IAP的最后结果是同时考虑了聚类需求和两个软约束罚值的折中解，从根本上保证其最终目的是使得式（5）最大. 而FHO-OAP算法则是在OAP聚类结束之后才计算罚值，这就导致软约束并未直接参与聚类过程，所以FHO-OAP算法并没有 FHO-IAP算法聚类效果好.

图7显示了6种聚类算法随K值变化的聚类效果变化趋势，图7中彩色面积表示的是各算法计算出性能指标的方差（即表3中括号内的数值）.

图7表明，当K ≤5时，IKM算法、FHO-IAP算法和 FHO-OAP算法的聚类效果较好，但随着 K 的增加，这3个算法的性能差距逐渐增大. 具体而言，由于IKM 对初始解的依赖严重，当K逐渐增大时，初始解的随机性变大，故所得结果的方差变大，说明IKM算法在 K值较大时聚类效果极不稳定. 相较而言，FHO-OAP 算法和FHO-IAP算法在K值较大时依旧保持了较好的结果和较高的稳健性.

此外，图7中ALC的聚类效果呈现出明显的不稳定性. 这是由于ALC 的聚类过程只考虑了类间平均距离，完全没有考虑两个软约束的需求，故其聚类结果极易受到软约束罚值的影响. 当K = 2，4，5时，ALC 的聚类结果违反软约束的程度更加严重，故相应软约束的罚值更大，直接拉低了ALC的整体性能.

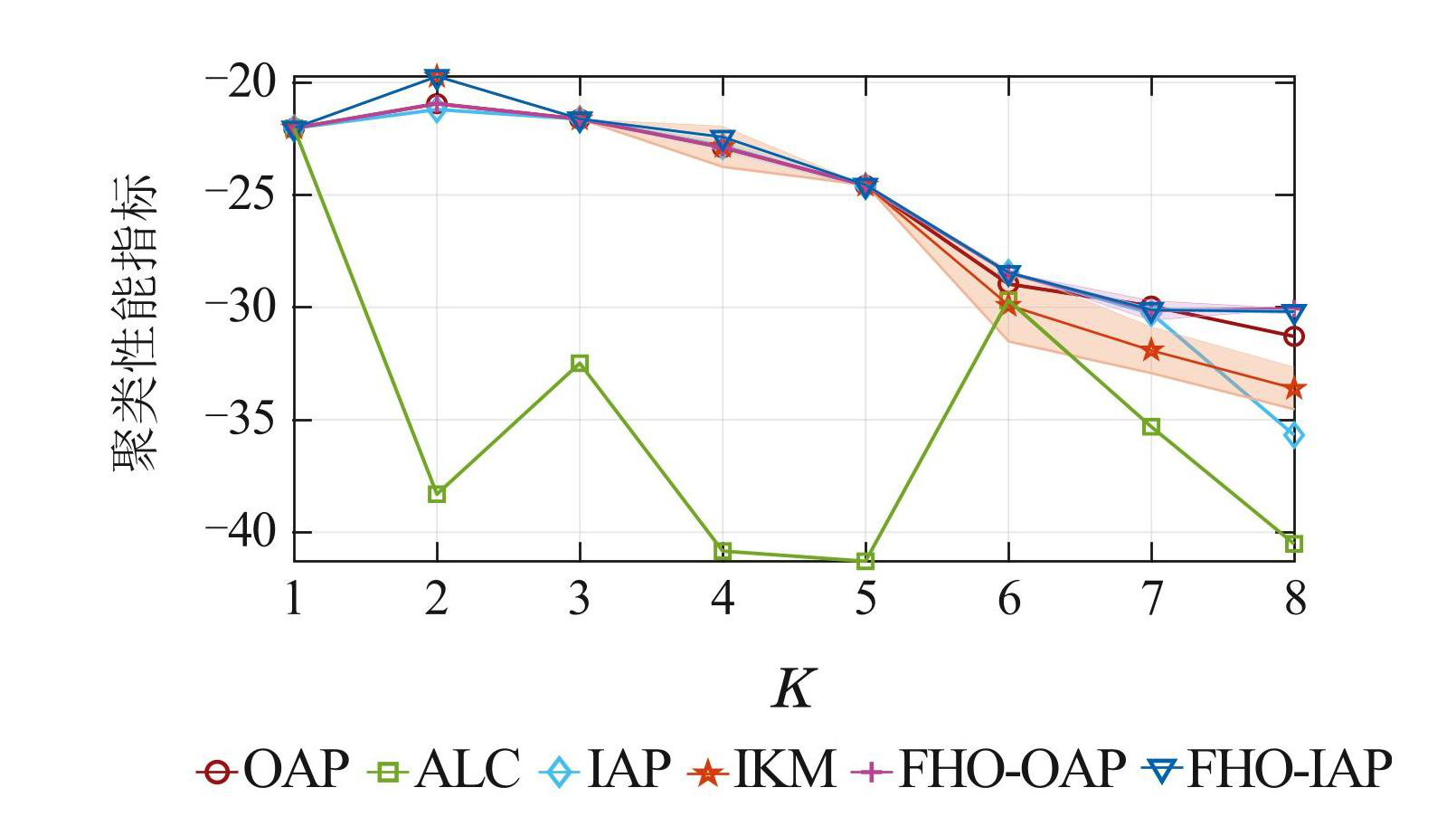
图7各算法的聚类效果比较

Fig.7Clustering result comparisons of each algorithm

综上所述，本文所提FHO-OAP和FHO-IAP相较于原始算法都有了明显的性能提升，说明FHO的引入确实能帮助AP算法自动选择最合适的参数. 此外，表3也表明FHO-IAP表现出最好的聚类效果，因为其性能平均排名（Rank）最低. 同时，FHO-IAP的方差也相对较小，体现了其在不同情况和需求的典型工艺路线发现问题上都具有较强的稳健性.

6 结语

本文提出了一种典型网状工艺路线的自动化发现方法: 1）设计了一种多维工艺信息融合的新型网状工艺路线综合相似度度量，以更加细粒度地量化网状工艺路线间的共有工艺信息; 2）在考虑聚类有效性的同时，基于FHO优化AP来自动化发现典型网状工艺路线，以保证所得典型工艺路线的质量.

为了有效量化网状工艺路线中的4种工艺信息，本文设计了双结构矩阵和KM算法来同时度量工序间相似度和先后顺序关系; 采用了Jaccard相似度来衡量共同工序数，而结构复杂度则通过可选工艺路线条数来量化. 最后，基于PCA分析了这些信息的相关性，并得到综合相似度度量.

另一方面，本文在考虑聚类有效性的基础上为典型网状工艺路线发现问题引入了数量软约束与半径软约束，以保证聚类结果的真实有效. 同时，为了解决 AP算法的参考度与阻尼系数无法自动调优问题，将 FHO引入其中. 相关实验也表明，FHO确实可以提高相应AP算法的聚类效果，其中FHO-IAP算法具有更好的聚类效果和更强的稳健性.

当然，本文所提方法还存在一些问题需要解决:

1）本文所提相似度度量无法解决重复工序的情况;

2）本文发现聚类过程倾向于选择结构更复杂的工艺路线，但过于复杂的典型工艺路线虽然能提供更多的信息，反而会降低辅助工艺规划的效果.

图1网状工艺路线的信息需求分析

Fig.1Information requirement analysis of the networked process routes

下载: 全尺寸图片

图2网状工艺路线的不同相似情况

Fig.2Different similar cases of the networked process routes

下载: 全尺寸图片

图3所需信息和相似度度量之间的层次关系

Fig.3The hierarchical relationship between the required information and the similarity measures

下载: 全尺寸图片

图4双结构矩阵

Fig.4Dual structure matrix

下载: 全尺寸图片

图5FHO-AP算法流程图

Fig.5Flow chart of the FHO-AP algorithm

下载: 全尺寸图片

图6网状工艺路线相似度度量计算结果比较

Fig.6Calculation result comparisons of the similarity measures for the networked process route

下载: 全尺寸图片

图7各算法的聚类效果比较

Fig.7Clustering result comparisons of each algorithm

下载: 全尺寸图片

表13种不同相似情况

Table1Three different similar situations

下载: 全尺寸图片

表23个中间相似度的主成分分析结果

Table2Principal component analysis results of three intermediate similarities

下载: 全尺寸图片

表340条网状工艺路线数据集的聚类结果与方差

Table3Clustering results and variance of 40 networked process route data set

下载: 全尺寸图片

图1网状工艺路线的信息需求分析

Fig.1Information requirement analysis of the networked process routes

图2网状工艺路线的不同相似情况

Fig.2Different similar cases of the networked process routes

图3所需信息和相似度度量之间的层次关系

Fig.3The hierarchical relationship between the required information and the similarity measures

图4双结构矩阵

Fig.4Dual structure matrix

图5FHO-AP算法流程图

Fig.5Flow chart of the FHO-AP algorithm

图6网状工艺路线相似度度量计算结果比较

Fig.6Calculation result comparisons of the similarity measures for the networked process route

图7各算法的聚类效果比较

Fig.7Clustering result comparisons of each algorithm

表13种不同相似情况

Table1Three different similar situations

表23个中间相似度的主成分分析结果

Table2Principal component analysis results of three intermediate similarities

表340条网状工艺路线数据集的聚类结果与方差

Table3Clustering results and variance of 40 networked process route data set

图1网状工艺路线的信息需求分析

Fig.1Information requirement analysis of the networked process routes

图2网状工艺路线的不同相似情况

Fig.2Different similar cases of the networked process routes

图3所需信息和相似度度量之间的层次关系

Fig.3The hierarchical relationship between the required information and the similarity measures

图4双结构矩阵

Fig.4Dual structure matrix

图5FHO-AP算法流程图

Fig.5Flow chart of the FHO-AP algorithm

图6网状工艺路线相似度度量计算结果比较

Fig.6Calculation result comparisons of the similarity measures for the networked process route

图7各算法的聚类效果比较

Fig.7Clustering result comparisons of each algorithm

表13种不同相似情况

Table1Three different similar situations

表23个中间相似度的主成分分析结果

Table2Principal component analysis results of three intermediate similarities

表340条网状工艺路线数据集的聚类结果与方差

Table3Clustering results and variance of 40 networked process route data set

XIAO Y, ZHENG S, SHI J,et al. Knowledge graph-based manufacturing process planning: A state-of-the-art review. Journal of Manufacturing Systems,2023,70:417-435.

GE Ruifu, REN Zhigang, LI Jianghao,et al. Construction method and application of knowledge graph for process defect of injection molding products. Control Theory & Applications,2024,41(3):577-585.(葛睿夫, 任志刚, 林江豪, 等. 面向注塑产品工艺缺陷的知识图谱构建方法及应用. 控制理论与应用,2024,41(3):577-585.)

DUAN J, DUAN Y. Toward a framework of extracting typical machining process routines based on knowledge representation learning. Advanced Engineering Informatics,2024,60:102431.

THANOS C, MEGHINI C, BARTALESI V,et al. An exploratory approach to data driven knowledge creation. Journal of Big Data,2023,10(1):29.

ZHANG H, WANG W, ZHANG S,et al. A novel method based on deep reinforcement learning for machining process route planning. Robotics and Computer-Integrated Manufacturing,2024,86:102688.

LI C. Study on typical process route mining method based on multilevel longest common subsequence information entropy and intelligent clustering model. International Journal of Computer Integrated Manufacturing,2023,36(10):1416-1430.

LIU S N, TIAN T X, ZHANG M Z,et al. Applying hierarchical clustering to discover the typical process route. Materials Science Forum,2006,51(532/533):949-952.

ZHANG Hui, QIU Lemiao, ZHANG Shuyou,et al. Typical product process route extraction method based on intelligent clustering analysis. Computer Integrated Manufacturing System,2013,19(3):490-498.(张辉, 裘乐淼, 张树有, 等. 基于智能聚类分析的产品典型工艺路线提取方法. 计算机集成制造系统,2013,19(3):490-498.)

XIN Y, CHAN Y, LI W,et al. Refined simulation method for computer-aided process planning based on digital twin technology. Micromachines,2022,13(4):620.

ZHU Zhenyu. Automated discovery method for typical process knowledge of discrete manufacturing systems. Wuxi: Jiangnan University,2019.(朱震宇. 离散制造系统的典型工艺知识自动化发现方法. 无锡: 江南大学,2019.)

ZHOU D, DAI X. Integrating granular computing and bioinformatics technology for typical process routes elicitation: A process knowledge acquisition approach. Engineering Applications of Artificial Intelligence,2015,45:46-56.

CHOOBINEH F. A framework for the design of cellular manufacturing systems. The International Journal of Production Research,1988,26(7):1161-1172.

ZHOU D, DAI X. A method for discovering typical process sequence using granular computing and similarity algorithm based on part features. The International Journal of Advanced Manufacturing Technology,2015,78:1781-1793.

LIU S, ZHANG Z, TIAN X. A typical process route discovery method based on clustering analysis. The International Journal of Advanced Manufacturing Technology,2007,35:186-194.

XU B, WANG Y, JI Z. A novel operation sequence similarity-based approach for typical process route knowledge discovery. IEEE Access,2021,9:126801-126821.

NAVAEI J, ElMARAGHY H. Grouping part/product variants based on networked operations sequence. Journal of Manufacturing Systems,2016,38:63-76.

WU L, SUZUKI S. Cell formation design with improved similarity coefficient method and decomposed mathematical model. The International Journal of Advanced Manufacturing Technology,2015,79:1335-1352.

WANG Lin, ZHANG Yongjian, ZHONG Shisheng. Typical process discovery of satellite typical parts based on affinity propagation clustering. Computer Integrated Manufacturing Systems,2015,21(6):1469-1475.(王琳, 张永健, 钟诗胜. 基于近邻传播聚类的卫星典型构件典型工艺过程发现. 计算机集成制造系统,2015,21(6):1469-1475.)

WANG L, ZHANG Y, ZHONG S. Typical process discovery based on affinity propagation. Journal of Advanced Mechanical Design, Systems,and Manufacturing,2016,10(1):1-13.

XU Binzi. Research on knowledge based energy efficiency optimization method for discrete manufacturing system. Wuxi: Jiangnan University,2019.(徐彬梓. 基于知识的离散制造系统能效优化方法研究. 无锡: 江南大学,2019.)

GUO Y, LI W, XIAO L,et al. A prediction-based iterative KuhnMunkres approach for service vehicle reallocation in ride-hailing. International Journal of Production Research,2024,62(10):3690-3715.

JACCARD P. The distribution of the flora in the alpine zone. New phytologist,1912,11(2):37-50.

AZIZI M, TALATAHARI S, GANDOMI A H. Fire hawk optimizer: A novel metaheuristic algorithm. Artificial Intelligence Review,2023,56(1):287-363.

LI C. A novel framework for discovery and reuse of typical process route driven by symbolic entropy and intelligent optimisation algorithm. Plos One,2022,17(9):e0274532.

HUA Bao, ZHOU Bin, GU Xinghai,et al. Semantic similarity measurement of process table based on graph neural network. Computer Integrated Manufacturing Systems,2022,28(12):3805-3821.(花豹, 周彬, 顾星海, 等. 基于图神经网络的工艺表格语义相似性度量. 计算机集成制造系统,2022,28(12):3805-3821.)

KUHN H W. The Hungarian method for the assignment problem. Naval Research Logistics Quarterly,1955,2(1/2):83-97.

FREY B J, DUECK D. Clustering by passing messages between data points. Science,2007,315(5814):972-976.

WANG G, HUANG S, SHANG X,et al. Formation of part family for reconfigurable manufacturing systems considering by passing moves and idle machines. Journal of Manufacturing Systems,2016,41:120-129.

FRIEDMAN M. The use of ranks to avoid the assumption of normality implicit in the analysis of variance. Journal of the American Statistical Association,1937,32(200):675-701.