欢迎访问《控制理论与应用》期刊网站！

永磁同步电机直接模型预测控制电压矢量占空比优化策略

doi: 10.7641/CTA.2025.40587

许宇豪，乔社娟，肖海峰，李文真

西安航空学院电子工程学院, 陕西西安 710077

基金项目: 陕西省科学技术厅自然科学基础研究计划项目(2024JC–YBQN–0440), 陕西省教育厅项目(23JK0496)资助.

详细信息

作者简介

许宇豪博士,讲师,目前研究方向为Z源逆变器和交流电机控制,E-mail: xyuh7006@126.com;

乔社娟高级工程师,目前研究方向为永磁同步电机模型预测控制,E-mail: 201308001@xaau.edu.cn;

肖海峰教授,研究生导师,目前研究方向为永磁同步电机非线性控制,E-mail: xhfxhdq@xaau.edu.cn;

李文真博士,讲师,目前研究方向为电机无位置传感器控制,E-mail: wen-zhenl1991@163.com.

通信作者

许宇豪，E-mail: xyuh7006@126.com;Tel.:+8613992863673.

Voltage vector duty cycle optimization strategy for direct model predictive control of PMSM

XU Yu-hao ， QIAO She-juan ， XIAO Hai-feng ， LI Wen-zhen

School of Electronics Engineering, Xi’an Aeronautical University, Xi’an Shaanxi 710077 , China

Funds: Supported by the Natural Science Foundation of Shaanxi Province (CN) (2024JC–YBQN–0440) and the Natural Science Foundation of Shaanxi Provincial Department of Education (CN) (23JK0496)

摘要

永磁同步电机直接转矩控制和模型预测控制相结合产生的模型预测转矩控制具有控制简单和动态响应能力强的优点. 然而, 在控制周期内作用多个电压矢量消除稳态误差时存在电压矢量组合失效和占空比运算复杂的问题. 本文提出了一种永磁同步电机直接模型预测控制的电压矢量占空比优化策略, 以提高双电压矢量作用时间运算结果的有效性. 基于无差拍控制原理, 推导磁链矢量与电压矢量之间的关系, 将控制变量归一化为参考电压矢量, 解决了权重系数整定问题. 进而, 通过划分扇区子区域, 直接得到最优电压矢量组合. 最后, 基于矢量合成原理, 对电压矢量的作用时间提出了总和与比值约束条件, 保证每种电压矢量作用时间的合理性与合成电压矢量的有效性. 实验结果证明了所提方法具有比传统方法更好的稳态性能和良好的动态性能.

关键词

模型预测控制 / 永磁同步电机 / 参考电压矢量 / 作用时间

Abstract

Combining the direct torque control and the model predictive control, the model predictive torque control for permanent magnet synchronous motor has the advantages of simple control and high dynamic response. However, there are two problems of voltage vector combination failure and complex duty-cycle calculation when multiple voltage vectors are applied during the control cycle to eliminate steady-state errors. This paper proposes a voltage vector duty cycle optimization strategy for direct model predictive control of permanent magnet synchronous motor, which improves the effectiveness of the operation time of dual voltage vector. Based on the principle of deadbeat control, the relationship between magnetic flux vector and voltage vector is derived. The control target is normalized to the reference voltage vector, and thus solving the problem of tuning weighting factor. Furthermore, the optimal voltage vector combination can be directly obtained by dividing the sub-regions of the sector. Finally, a sum and a ratio constraint conditions are proposed for the action time of voltage vectors based on the principle of vector synthesis. Therefore, the rationality of each voltage vector and the effectiveness of synthesized voltage vector are improved. The experimental results indicate that the proposed method has better steady-state performance and good dynamic performance than the traditional methods.

Keywords

model predictive control / permanent magnet synchronous motor / reference voltage vector / duration time

1 引言 2 永磁同步电机的直接模型预测控制 2.1 控制方案 2.2 预测模型 2.3 成本函数 3 直接模型预测控制电压矢量占空比优化策略 3.1 控制原理 3.2 参考电压矢量定位 3.3 电压矢量作用时间分配方法 3.4 所提方法的优势分析 4 实验验证 4.1 速度稳态实验结果 4.2 速度阶跃实验结果 4.3 突加负载实验结果 5 结论

1 引言

随着数字信号处理器运算能力的不断提高，模型预测控制以其直观的概念、高动态响应能力和多变量灵活控制的优点较多地应用于永磁同步电机调速中 ^[1-2] . 根据优化方法的不同，模型预测控制分为有限集模型预测控制和连续集模型预测控制. 有限集模型预测控制是一种基于逆变器离散数学模型的控制算法，它能够在有限的几个开关状态中通过枚举法选择出一个最优的开关状态或者开关状态序列，因此它不需要调制器来产生脉冲宽度调制（pulse width modulation，PWM）驱动信号，同时还能够很好地解决逆变器的非线性问题.

在有限集模型预测控制中，直接模型预测转矩控制具有高动态响应能力和多变量灵活控制的优点，是永磁同步电机常用的模型预测控制方法之一. 根据电磁转矩和定子磁链未来状态，直接模型预测转矩控制在每个控制周期中选择一个最优电压矢量作用于逆变器. 然而，有限数量的电压矢量导致磁链和电磁转矩纹波较大，降低永磁同步电机（permanent magnet synchronous motor，PMSM）的稳态性能 ^[3-4] . 此外，成本函数中用于平衡电磁转矩和定子磁链的权重系数需要随系统工况而改变 ^[5-9]，降低了直接模型预测转矩控制的实用性.

依据矢量控制思想，学者们将控制周期内单一的电压矢量扩展为多个电压矢量的组合，并以不同的占空比作用于交流电机，构成最优开关序列. 虽然在控制周期内施加更多的电压矢量能够提高直接模型预测转矩控制的控制精度，然而控制策略的复杂度将随着电压矢量组合的增加而增加 ^[10-11] . 同时，该方法还存在串行选择电压矢量而导致的控制性能最优化问题. 为此，文献 ^[12-13] 依据定子磁链和定子电流的变化规律，直接选择最优的电压矢量. 然而，求解电压矢量的作用时间较为复杂. 因此，降低选取电压矢量组合的运算量，简化预选电压矢量流程成为当前研究的热点. 文献 ^[14-15] 通过增加虚拟电压矢量，将候选电压矢量从6个减少到2个. 文献 ^[16] 利用电压矢量序列的对称关系，从而将候选向量的数量从7个减少到1 个，但αβ–坐标系与dq–坐标系之间需要进行坐标变换.

为了避免权重系数整定带来的巨大试验工作量，文献 ^[17] 提出了一种多变量排序算法. 将多变量组成的成本函数分解为几个仅有单个控制变量的成本函数. 基于排序规则依次评估每个成本函数，以获得最优电压矢量. 然而，排序的实现流程与通过经验方法整定权重系数一样繁琐. 另一种消除权重系数的方法是对多个控制变量归一化. 文献 ^[18-20] 通过分析电磁转矩、定子磁链幅值和定子权重系数之间的关系，将多个控制变量简化为一个控制变量，成本函数仅包含定子磁链或参考电压矢量. 然而，电压矢量的作用时间很可能出现大于控制周期或小于零的不合理情况.

本文提出了一种永磁同步电机直接模型预测控制的电压矢量占空比优化策略，以提高双电压矢量作用时间的有效性，同时解决了多变量优化控制的权重系数整定问题. 首先，根据永磁同步电机数学模型，采用前向欧拉法推导了静止坐标系下的预测模型并给出成本函数. 然后，根据变量磁链和电磁转矩，采用无差拍控制导出参考电压矢量，实现控制变量归一化. 最后，分析电压矢量作用时间与控制周期的关系，提出电压矢量作用时间约束条件，从而导出每种电压矢量作用时间的表达式. 理论分析和实验结果表明，所提方法能保证电压矢量作用时间始终在有效范围内，避免了作用无效的电压矢量组合，具有较好的稳态和动态性能. 本文所提方法的主要创新点如下:

1）将系统中的多被控量转化为单一电压矢量控制，实现控制变量归一化，并解决了权重系数整定问题;

2）提出了扇区区域划分方法，无需成本函数可直接得到最优电压矢量组合，提高了直接模型预测控制的运算效率;

3）在电压矢量合成方法基础上，融入了作用时间总和与比值约束条件，避免了双矢量模型预测控制作用无效电压矢量组合的问题. 该方法能确保合成电压矢量的有效性，提高永磁同步电机的稳态性能.

2 永磁同步电机的直接模型预测控制

直接模型预测控制是一种基于永磁同步电机模型的预测控制方法，通过离散化电气方程和运动方程，预测电机控制系统未来时刻的状态，并在可施加的开关组合下寻找最优解. 本节给出了直接模型预测控制的基本原理，推导了磁链和转矩的预测模型，分析了输出状态最优化的实现方案.

2.1 控制方案

三相两电平逆变器驱动永磁同步电机的拓扑结构如图1所示. 通过PWM驱动三相逆变器的开关器件，可由逆变器输出三相正弦交流电压，从而在永磁同步电机定子侧产生一个圆形旋转磁场，吸引着转子按照同步速度旋转.

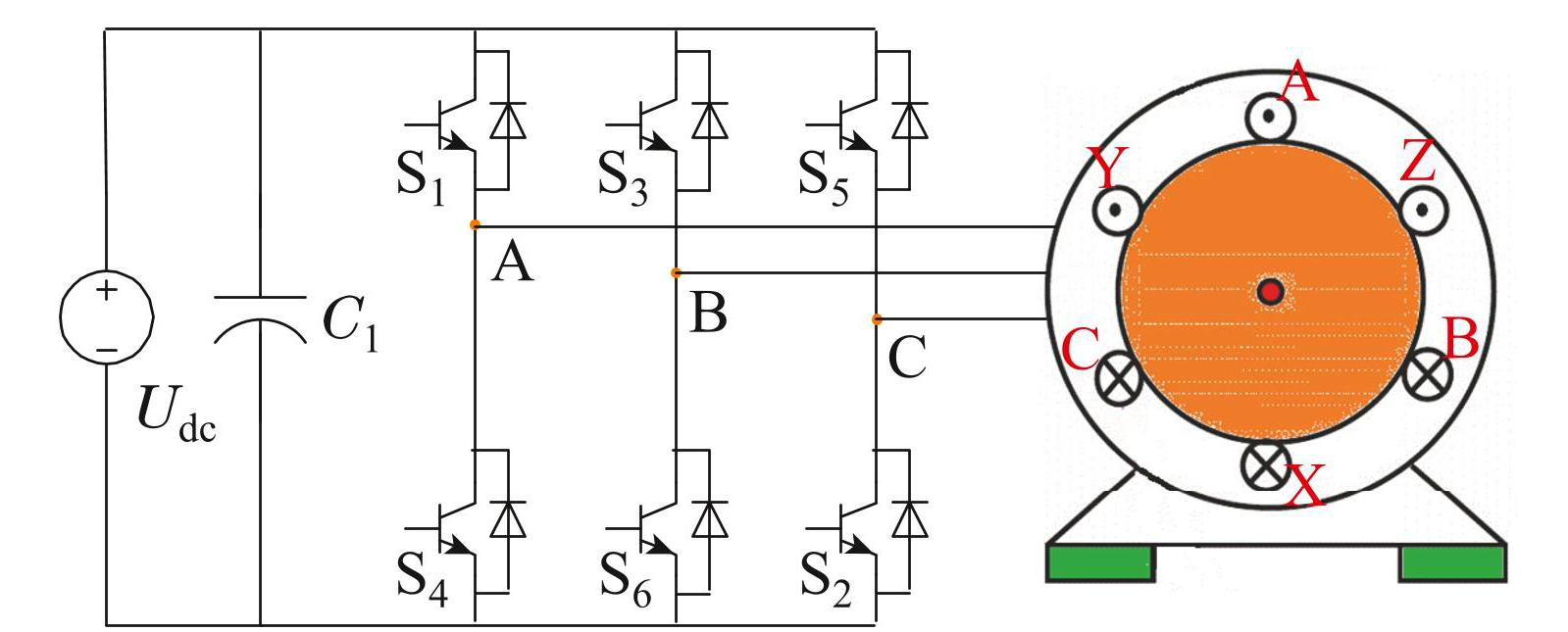
图1三相两电平逆变器驱动永磁同步电机拓扑

Fig.1Topology of permanent magnet synchronous motor driven by three-phase two-level inverter

永磁同步电机调速的关键核心问题在于施加的 PWM信号的品质，这也是由其控制方案所决定的. 不论是工业界常采用的矢量控制还是直接转矩控制，或是近年来研究较热的直接模型预测控制都能为永磁同步电机提供高品质的PWM驱动信号. 如图2所示，直接模型预测控制的结构包含了两层控制回路，外环为速度环，内环为力矩和磁链环. 速度环采用比例积分（proportion integral，PI）调节器控制，将反馈速度与参考速度比较后，通过PI调节器生成转矩控制信号. 在力矩和磁链环中，将采样得到的永磁同步电机三相电流变换到两相旋转坐标系下，利用电流、磁链和转矩的预测模型依次计算出下一时刻的预测电流、预测磁链和预测转矩; 基于最优化理论，把不同输出的电压矢量对应的预测磁链和预测转矩与它们的参考指令进行比较与评价，最终施加综合性能最佳的电压矢量. 其中: automatic speed regulator（ASR）为速度调节器，voltage source inverter（VSI）是电压源型逆变器，dq/ABC是将ABC坐标系的电流变换到dq坐标系下.

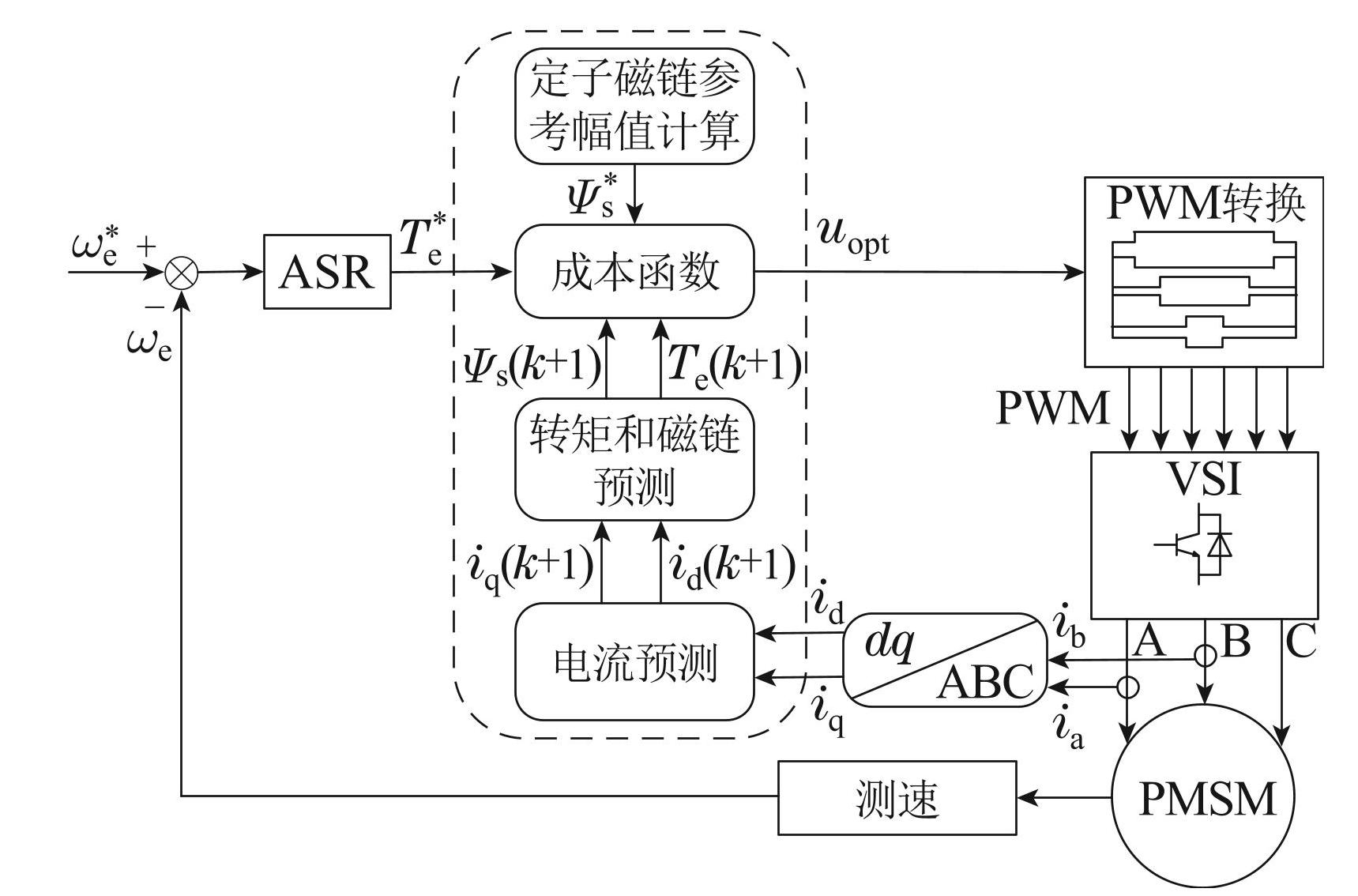
图2直接模型预测控制方案

Fig.2Direct model predictive control scheme

2.2 预测模型

为了减少旋转坐标变换带来的计算负担，系统的建模采用两相静止坐标系. αβ–坐标系和dq–坐标系分别指代定子静止坐标系和转子同步旋转坐标系. 永磁同步电机在αβ–坐标系的方程可以表示为

u_{s} = R_{s} i_{s} + \frac{d ψ_{s}}{d t},

(1)

ψ_{s} = L_{s} i_{s} + ψ_{f} e^{j θ_{r}},

(2)

T_{e} = \frac{3 n_{p}}{2 L_{s}} ψ_{f} |ψ_{s}| s i n δ_{s r}

(3)

式中: u_s，i_s，ψ_s和ψ_f分别是定子电压矢量、定子电流矢量、定子磁链和转子磁链，u_s= [u_α u_β]^T，i_s = [i_α i_β]^T，ψ_s = [ψ_α ψ_β]^T; R_s，θ_r和L_s分别为定子电阻、定子电压矢量角和定子电感; T_e，n_p和δ_sr分别是电磁转矩、极对数和定子磁链角.

永磁同步电机控制系统的预测模型建立在离散时间域. 将式（2）代入式（1）并采用前向欧拉方法可得到定子电流矢量的预测值为

\{\begin{array}{l} i_{sp} (k + 1) = \\ i_{s} (k) + \frac{T_{s}}{L_{s}} (u_{s} (k) - R_{s} i_{s} (k) - j ω ψ_{f} e^{j θ_{r}}), \\ i_{s} (k + 1) = \\ i_{sp} (k + 1) - \frac{T_{s} R_{s}}{2 L_{s}} (i_{sp} (k + 1) - i_{s} (k)), \end{array}

(4)

式中: k和k+1分别表示当前时刻和下一时刻，i_sp（k+ 1）是预测定子电流矢量，i_s（k + 1）是预测校正定子电流矢量，T_s是采样时间，ω是电角速度.

基于式（2）–（3），定子磁链和电磁转矩的预测模型可表示为

ψ_{s} (k + 1) = L_{s} i_{s} (k + 1) + ψ_{f} e^{j θ_{r}},

(5)

T_{e} (k + 1) = \frac{3 n_{p}}{2 L_{s}} ψ_{f} |ψ_{s} (k + 1)| s i n δ_{s r} .

(6)

考虑到数字控制器产生的一拍延迟，这将导致通过模型预测控制得到的当前时刻电压矢量延迟到下一时刻才能输出. 因此，补偿一拍延迟对低采样频率的控制系统尤为重要. 采用一步延迟补偿将式（5）–（6）中所表示的k + 1时刻预测值再递推一个时刻，消除表达式中k时刻变量. 补偿延迟后的定子磁链和电磁转矩预测模型可表示为

\begin{matrix} ψ_{s} (k + 2) = ψ_{s} (k + 1) + T_{s} [u_{s} (k + 1) - \\ R_{s} i_{s} (k + 1)], \end{matrix}

(7)

T_{e} (k + 2) = \frac{3 n_{p}}{2 L_{s}} ψ_{f} |ψ_{s} (k + 2)| s i n δ_{s r} .

(8)

2.3 成本函数

电磁转矩与定子磁链的是直接模型预测转矩控制的控制变量，考虑时间延迟补偿的直接模型预测转矩控制的成本函数定义为

g = |T_{e}^{*} - T_{e} (k + 2)| + λ_{ψ} | | ψ_{s}^{*} |- |ψ_{s} (k + 2)||,

(9)

式中: λ_ψ是成本函数的权重系数，

T_{e}^{*}

和

ψ_{s}^{*}

分别是αβ 坐标系中电磁转矩和定子磁链的参考值. 在式（9）中，通过将8个基本电压矢量带入成本函数，可计算出使成本函数值最小化对应的最优电压矢量. 由于电磁转矩和定子磁链量纲不同且对永磁同步电机控制重要性不同，需通过大量的实验才能得到合适的权重系数.

3 直接模型预测控制电压矢量占空比优化策略

直接模型预测控制具有动态响应迅速的优势，但由于作用电压矢量单一而导致了稳态误差大的缺点. 借鉴于矢量控制提高永磁同步电机稳态控制性能的思想，本节将直接模型预测控制与矢量控制的优势融合. 在采用直接模型预测控制前提下，在一个控制周期作用多个不同占空比的电压矢量，确保控制系统具有良好的动态和稳态性能. 同时，针对如何选取最优电压矢量组合并计算其持续时间的关键问题展开研究，提出了直接模型预测控制的电压矢量占空比优化策略.

3.1 控制原理

在基于双矢量的模型预测控制方法中，作用于逆变器的合成电压矢量应尽可能接近参考矢量，以提高控制精度. 该方法的关键步骤是通过计算所施加电压矢量序列和持续时间来调整合成电压矢量的幅度和相位. 然而，双矢量选择的运算量大、电压矢量作用总时间易超出控制周期的时间范围等缺点降低了系统的稳态性能. 因此，在所提出的方法中，采用调制手段计算电压矢量作用时间.

本文所提方法的控制结构框图主要由3部分组成，如图3所示. 首先，与传统方案不同，所提方法将电流和磁链的预测建立在静止αβ–坐标系下，可以避免复杂的坐标变换运算，以及由位置检测不准确导致的电流预测偏差. 然后，根据无差拍控制原理，将外环PI控制器得到的参考转矩指令用于计算磁链参考指令和负载角，利用磁链的空间几何关系分析定子磁链分量的参考值. 最后，由定子磁链和定子电压的关系，导出电压矢量的参考值. 在确定参考电压矢量所在扇区的前提下，将其相邻的电压矢量和零矢量组合，构成3组候选电压矢量组合. 通过确定参考电压矢量落入的扇区子区域，可直接得到最优电压矢量组合.

图3直接模型预测控制电压矢量占空比优化策略

Fig.3Voltage vector duty cycle optimization strategy for direct model predictive control

3.2 参考电压矢量定位

基于无差拍控制原理，令式（7）–（8）中的转矩预测值T_e（k + 2）和定子磁通预测值Ψ_s（k + 2）等于它们的参考值

T_{e}^{*}

和

ψ_{s}^{*}

. 定子磁链角的参考指令可推导为

δ_{s r}^{*} = a r c s i n \frac{2 L_{s} T_{e}^{*}}{3 n_{p} ψ_{f} |ψ_{s}^{*}|},

(10)

式中|

ψ_{s}^{*}

|是定子磁链参考指令的幅值，表示为|

ψ_{s}^{*}

| =

\sqrt{ψ_{f}^{2} + {(\frac{2 L_{s} T_{e}^{*}}{3 n_{p} ψ_{f}})}^{2}} .

. 定子磁链在αβ–坐标系可表示为

ψ_{s}^{*} = |ψ_{s}^{*}| e^{j (δ_{s r}^{*} + θ_{r})}

(11)

令式（7）中的ψ_s（k + 2）等于定子磁链参考指令，可导出参考电压矢量为

u_{s}^{*} = R_{s} i_{s} (k + 1) + \frac{1}{T_{s}} (ψ_{s}^{*} - ψ_{s} (k + 1)),

(12)

式中

u_{s}^{*} = {[\begin{matrix} u_{α}^{*} u_{β}^{*} \end{matrix}]}^{T}

. 根据式（12）给出了定子磁链和电压矢量的关系，利用基本电压矢量合成参考电压矢量

u_{s}^{*}

就能产生参考定子磁链. 因此，通过式（12）得到参考电压矢量

u_{s}^{*}

后，下一步将通过矢量合成方法寻找基本电压矢量合成

u_{s}^{*}

. 参考电压矢量的角度

θ_{u}^{*}

可表示为

θ_{u}^{*} = a r c t a n \frac{u_{β}^{*}}{u_{α}^{*}}

(13)

从式（12）–（13）可以看出，通过推导磁链矢量关系式，可将磁链和转矩这两个被控量转化为唯一的电压矢量. 控制变量的归一化能避免采用成本函数整定权重系数的繁琐流程，这是本文的创新点之一，也为下文所提的扇区区域划分方法提供了必要条件.

在式（13）中，由参考电压矢量的角度可以直接定位参考电压矢量所在的扇区. 然而，现有文献通常将扇区相邻的有效电压矢量和零电压矢量组合，构成3 种电压矢量组合，再利用成本函数得到最优的电压矢量组合. 这种方法不能完成直接寻优的目的，所产生的计算量较大. 为此，本文采用了扇区区域划分的方法简化该计算过程，如图4所示.

扇区的中心位于O点，依次将扇区三角形的3个顶点与中心连接，构成了扇区的3个区域. 当参考电压矢量位于区域1时，电压矢量u₂和u₃的组合要比u₀与u₃ 和u₂与u₀的组合所产生的误差小; 当参考电压矢量位于区域2时，电压矢量u₀与u₃的组合要比u₀与u₂和 u₂与u₃的组合所产生的误差小; 当参考电压矢量位于区域3时，电压矢量u₂和u₀的组合要比u₀与u₃和 u₂与u₃的组合所产生的误差小. 由此可知，只需要通过判断参考电压矢量的区域就能直接得到最优电压矢量组合，无需在通过成本函数的计算.

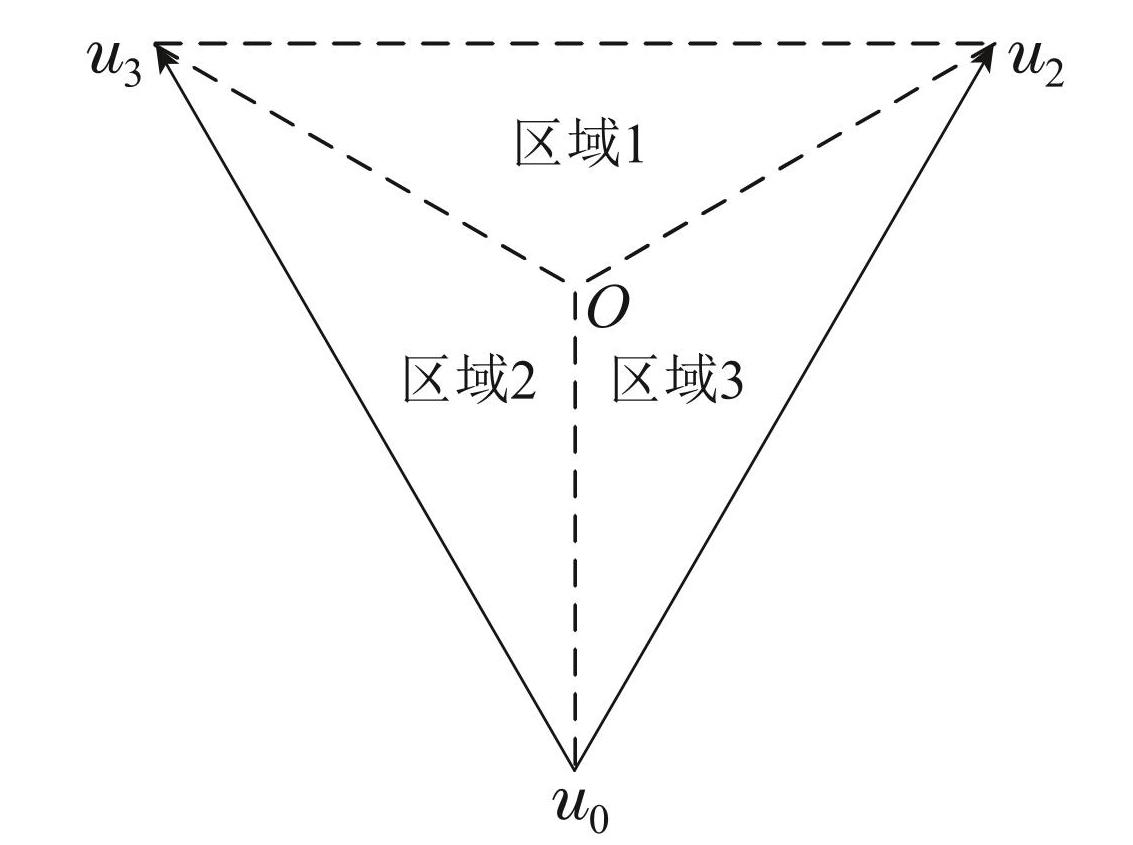
图4参考电压矢量所在扇区的划分示意图

Fig.4Schematic diagram of sector division where reference voltage vector is located

通过分析电压矢量合成机理中参考电压矢量所处扇区位置对电压矢量组成的影响，将每个扇区划分为 3个子区域，并建立新的电压矢量筛选机制. 该方法提高了直接模型预测控制的运算效率，是本文的第2个创新点.

3.3 电压矢量作用时间分配方法

假设永磁体磁链在每个控制周期保持不变，那么永磁同步电机绕组的端电压远小于逆变器的输出电压. 基于无差拍控制，式（7）中的定子磁链可推导为

T_{s} u_{s}^{*} = ψ_{s}^{*} (k + 2) - ψ_{s} (k + 1) .

(14)

使用前向欧拉法离散化式（7），则式（6）可进一步推导为

\begin{matrix} ψ_{s}^{*} (k + 2) - ψ_{s} (k + 1) = \\ K (T_{e}^{*} (k + 2) - T_{e} (k + 1)), \end{matrix}

(15)

式中

K = \frac{2 L_{s}}{3 n_{p} ψ_{f}}

从式（14）–（15）可以看出，控制变量可从转矩和定子磁链的误差转换为电压矢量误差，所施加的电压矢量越接近参考电压矢量，转矩波动和磁链波动就越小. 因此，在所提方法成本函数中直接使用电压矢量作为控制变量，并附加定子电流的硬件限制保护，成本函数的表达式为

\begin{matrix} g = |u_{s}^{*} - u_{s} (k + 1)| + I_{m} (k + 1) = \\ |u_{s}^{*} - (\frac{t_{o p t 1}}{T_{s}} u_{o p t 1} + \frac{t_{o p t 2}}{T_{s}} u_{o p t 2})| + I_{s m} (k + 1), \end{matrix}

(16)

式中: u_s（k + 1）是预测输出电压矢量在αβ轴的分量，由两个基本电压矢量合成; u_opt1和u_opt2是由式（12）选择出的两个最优电压矢量的组合; t_opt1和t_opt2是电压矢量u_opt1和u_opt2的作用时间. 式（16）利用求解最优化问题原理实现合成电压矢量逼近参考电压矢量，此时式（16）取得最小值，最优化问题得以求解. 电流限幅值I_sm，可表示为

I_{s m} (k + 2) = \{\begin{matrix} 0, |i_{s} (k + 1)| ⩽ |i_{s m a x}|, \\ \infty, |i_{s} (k + 1)| > |i_{s m a x}| . \end{matrix}

(17)

图5给出了如何利用平行四边形法则合成电压矢量的例子. 经过第2.2节的扇区区域划分后，基本电压矢量u₂和u₃将被作为最优电压矢量u_opt1 和u_opt2，作用时间分别为t_opt1和t_opt2，产生了120度方向的电压矢量t_opt1u_opt1/T_s和60度方向的电压矢量t_opt2u_opt2/ T_s . 根据平行四边形法则，调整t_opt1和t_opt2可合成参考电压矢量

u_{s}^{*}

. 合成的参考电压矢量可表示为

u_{s}^{*} = \frac{t_{o p t 1}}{T_{s}} u_{o p t 1} + \frac{t_{o p t 2}}{T_{s}} u_{o p t 2},

(18)

式中u_s是由最优电压矢量组合合成的电压矢量. 通过在每个控制周期中调整每种电压矢量的作用时间，合成矢量u_s可以最大限度趋近于参考矢量

u_{s}^{*}

. 考虑到电压矢量的作用时间非负且不能超过控制周期，所有电压矢量作用时间总和应该等于控制周期，满足约束条件

T_{s} = t_{o p t 1} + t_{o p t 2} .

(19)

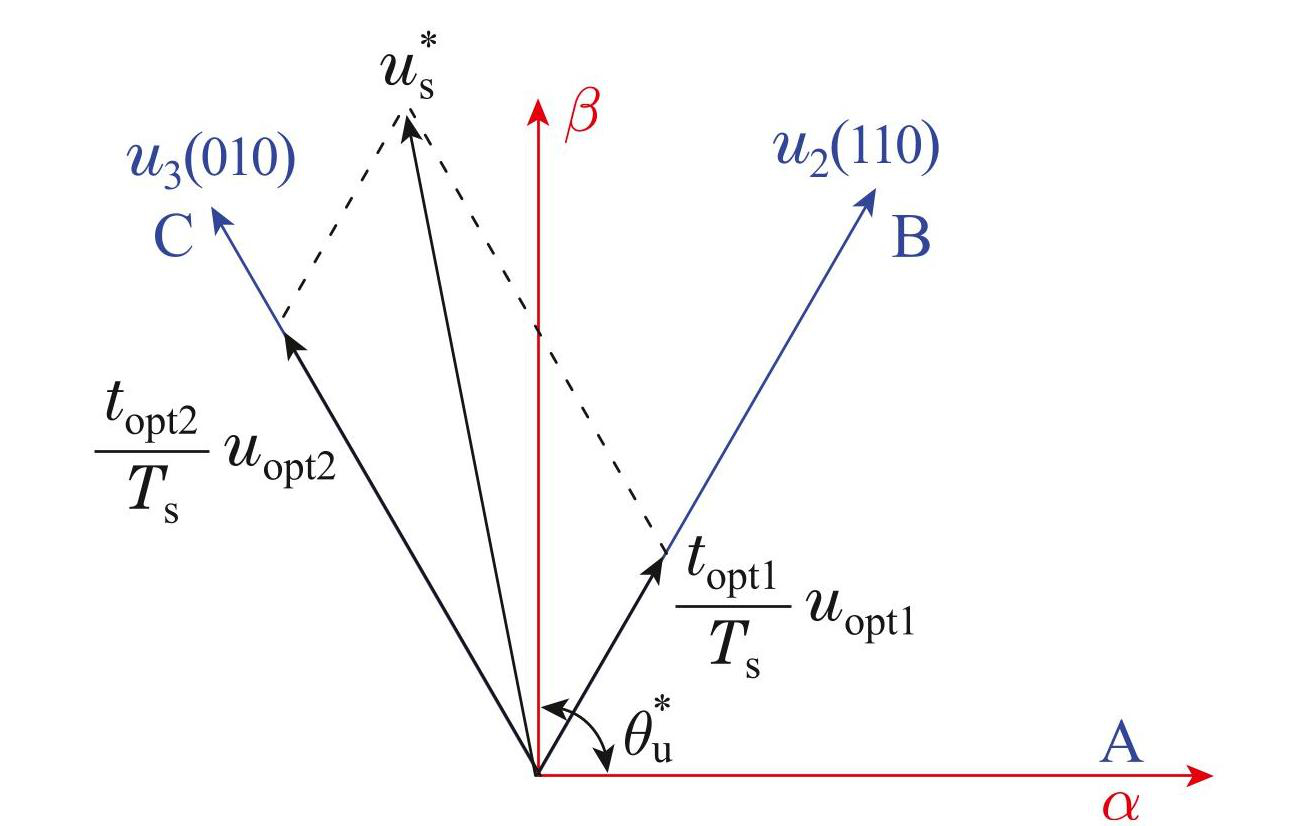
图5候选电压矢量合成图

Fig.5Candidate voltage vector synthesis diagram

通过求解式（18）–（19），电压矢量的作用时间可表示为

\{\begin{matrix} t_{o p t 1} = \frac{|u_{s}^{*} - u_{o p t 2}|}{|u_{o p t 1} - u_{o p t 2}|} T_{s}, \\ t_{o p t 2} = \frac{|u_{s}^{*} - u_{o p t 1}|}{|u_{o p t 1} - u_{o p t 2}|} T_{s}, \end{matrix}

(20)

t_opt1和t_opt2的比值为

\frac{t_{o p t 1}}{t_{o p t 2}} = \frac{|u_{s}^{*} - u_{o p t 2}|}{|u_{s}^{*} - u_{o p t 1}|} .

(21)

由式（21）可看出，电压矢量作用时间与其误差成反比. 只要满足式（18）–（19），电压矢量的作用时间就是有效的. 此外，电压矢量作用时间应小于控制周期. 通过使用电压误差的绝对值来代替电压误差，式（21）可改写为

\{\begin{matrix} t_{o p t 1} = \frac{|u_{s}^{*} - u_{o p t 2}|}{|u_{s}^{*} - u_{o p t 1}| + |u_{s}^{*} - u_{o p t 2}|} T_{s}, \\ t_{o p t 2} = \frac{|u_{s}^{*} - u_{o p t 1}|}{|u_{s}^{*} - u_{o p t 1}| + |u_{s}^{*} - u_{o p t 2}|} T_{s} . \end{matrix}

(22)

从式（22）可以看出，0 ≤ t_opt1 ≤ T_s，0≤t_opt2 ≤T_s，满足式（18）–（19）的约束条件. 因此，所提出的方法具有两个明显优势: 第一，成本函数不含权重系数. 第二，电压矢量作用时间始终在有效范围内，避免了作用无效的电压矢量组合，这是本文的第3个创新点.

3.4 所提方法的优势分析

近年来，施加多电压矢量已成为提高直接模型预测控制性能的常用方法. 在基于多矢量的直接模型预测控制中，电压矢量组合及作用时间是影响控制性能的主要因素. 然而，采用串行多步实现该过程不能保证最优控制的全局性. 本节将所提出方法与近年提出的基于多矢量直接模型预测控制方法在计算电压矢量作用时间方面进行了比较.

虽然合理分配电压矢量的作用时间对于直接模型预测控制有着重要作用，但是目前的研究主要集中在电压矢量的选择上，还没有形成统一的方法计算作用时间. 文献 ^[12，19-20] 分别提出了3种直接模型预测控制电压矢量作用时间的经典方法，即无差拍转矩控制、磁链脉动最小化控制和电压矢量误差最小化控制. 这3种方法的电压矢量作用时间表达式为

\begin{matrix} t_{o p t 1} = \\ \frac{2 T_{e}^{*} / (3 n_{p}) - T_{s} [u_{o p t 1} \otimes i_{s} (k + 1)]}{(u_{o p t 1} - u_{o p t 2}) \otimes i_{s} (k + 1)} - \\ \frac{[ψ_{s} (k + 1) - R_{s} i_{s} (k + 1) T_{s}] \otimes i_{s} (k + 1)}{(u_{o p t 1} - u_{o p t 2}) \otimes i_{s} (k + 1)}, \end{matrix}

(23)

\begin{matrix} t_{o p t 1} = \\ \frac{[|ψ_{s}^{*}| - |ψ_{s} (k + 1)| - R_{s} i_{s} (k + 1) T_{s} - u_{o p t 2} T_{s}]}{{|u_{o p t 1} - u_{o p t 2}|}^{2}} \\ \frac{(u_{o p t 1} - u_{o p t 2})}{{|u_{o p t 1} - u_{o p t 2}|}^{2}}, \end{matrix}

(24)

t_{o p t 1} = \frac{(u_{s}^{*} - u_{o p t 2} T_{s}) ⊙ (u_{o p t 1} - u_{o p t 2})}{{|u_{o p t 2} - u_{o p t 1}|}^{2}},

(25)

式中: ⊗表示电压矢量的叉积运算，⊙表示电压矢量的点积运算. 由式（23）–（25）和式（22）的对比可知，所提出的方法具有以下优点:

1）所提方法电压矢量作用时间的表达式含有较少的电机参考，因此具有较强的参数鲁棒，并且计算复杂度低于其他3种方法;

2）与其他3种方法通过级联方式获取电压矢量及其作用时间相比，所提方法可同步获得作用时间和最优电压矢量，兼顾控制全局最优性;

3）所提方法的电压矢量作用时间在0和Ts之间变化，保证了作用双电压矢量的有效性. 然而，其他3种方法的电压矢量作用时间存在超出该范围的情况，导致在整个控制周期中仅施加了一个电压矢量，产生较大的转矩和磁链脉动.

4 实验验证

为验证所提方法的可行性和正确性，本文搭建了永磁同步电机对拖实验平台，如图6所示. 平台采用涡流制动器作为负载，为永磁同步电机产生所需的负载转矩. 控制算法在数字信号处理器TMS320F28335实现. 永磁同步电机的额定电压为 220 V，额定电流为 8.8 A，额定功率为 2 kW，磁极对数为 5，额定转速为 1500 r/min，额定转矩12.7 N·m，定子电感12 mH，定子电阻0.84 Ω，采样频率为25 kHz.

图6永磁同步电机对拖实验平台

Fig.6Permanent magnet synchronous motor experimental platform

由于文献 ^[19-20] 中的方法在近5年文献中较多被采用，在基于多电压矢量的直接模型预测控制方法中具有较强代表性. 文献 ^[19-20] 与本文同隶属于永磁同步电机的模型预测控制方法研究，从被控对象、控制方法、引用场景均具有高度相似性. 因此，采用这两篇文献作为实验对比对象.

4.1 速度稳态实验结果

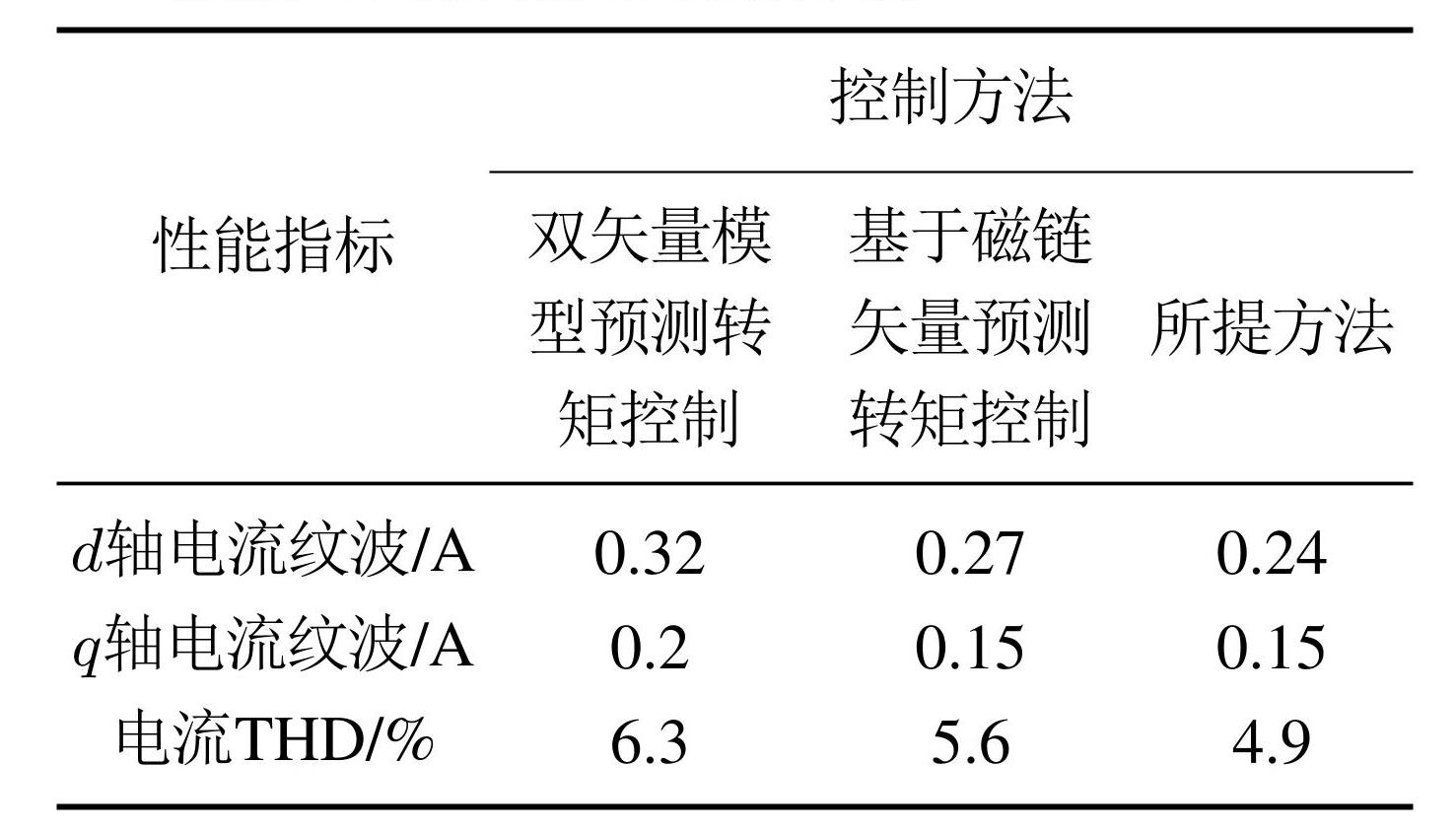
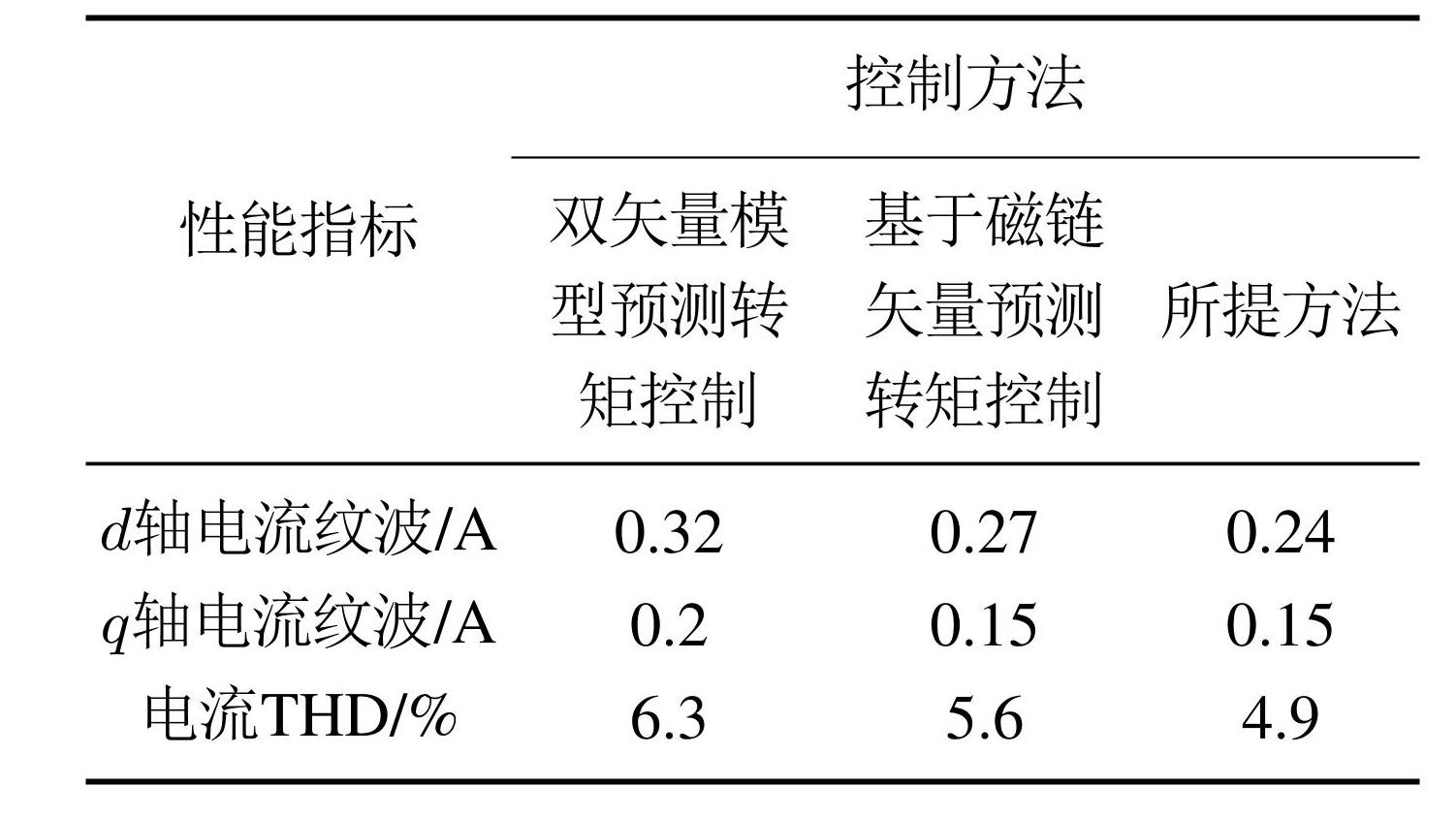
图7给出了双矢量模型预测转矩控制 ^[19]、基于磁链矢量的预测转矩控制 ^[20] 和本文所提出方法在 1500 r/min的稳态实验结果. 在1500 r/min的转速下，双矢量模型预测转矩控制、基于磁链矢量的预测转矩控制和所提的方法的 d 轴电流纹波分别为 0.32 A、 0.27 A和 0.24 A，而q 轴电流纹波则分别为 0.2 A、 0.15 A和0.15 A. 可以看出，d轴和q轴的电流波纹与采用的控制方法密切相关，所提方法的d轴电流纹波和q轴电流纹最小. 采用3种方法产生的电流总谐波失真（total harmonic distortion，THD）分别为6.3%，5.6% 和4.9%. 采用所提方法产生的电流THD小于采用双矢量模型预测转矩控制、基于磁链矢量的预测转矩控制所产生的电流THD. 所提方法的稳态性能优于双矢量模型预测转矩控制和基于磁链矢量的预测转矩控制.3种方法的稳态实验结果总结在表1中.

图7稳态实验结果

Fig.7Steady state experimental results

表13种方法的稳态实验结果对比

Table1Comparison of steady-state experimental results of the three methods

4.2 速度阶跃实验结果

图8给出了永磁同步电机转速在 0 r/min 和750 r/min之间变化的动态实验结果. 永磁同步电机的状态为从静止加速到750 r/min，保持约2 s后开始制动. 当速度参考值阶跃到750 r/min时，q 轴电流增加以提供正向加速转矩，加速和减速的动态过程持续约 0.65 s. 实验结果表明，双矢量模型预测转矩控制和基于磁链矢量的预测转矩控制、所提出方法都能很好地跟踪速度参考，d轴和q轴电流动态响应速度相近.3种方法的动态实验结果总结在表2中.

图8速度阶跃实验结果

Fig.8Experimental results of step change in speed

4.3 突加负载实验结果

图9给出了电机在80 r/min突加额定负载的动态响应实验结果. 突加额定负载时，A相电流和q轴电流的峰值分别增大到12.3 A和12.5 A，以平衡负载转矩和恢复转速降落值. 采用双矢量模型预测转矩控制，跟踪q轴电流参考值的动态时间需要105 ms. 采用基于磁链矢量的预测转矩控制和所提出的方法，q轴电流的暂态时间分别为80 ms和50 ms. 因此，所提出方法的q轴电流响应时间比双矢量模型预测转矩控制和基于磁链矢量的预测转矩控制快. 此外，在突然施加负载后，d轴电流和q轴电流的波动显著增加. 从动态加载实验结果可以看出，在重载情况下所提出的方法的电流响应时间比其他两种方法快，转速受到的影响最小.3种方法的动态实验结果总结在表2中.

表23种方法的动态实验结果对比

Table2Comparison of dynamic experimental results of the three methods

5 结论

为了避免直接模型预测转矩控制因电压矢量作用时间不合理而导致电压矢量合成失效的问题，提出了一种永磁同步电机直接模型预测控制的电压矢量占空比优化策略. 本文的主要工作和结论如下:

1）通过推导磁链矢量与参考电压矢量的关系，实现了控制变量归一化，避免了采用成本函数整定权重系数的繁琐流程.

2）提出了扇区子区域的划分方法，建立了新的电压矢量筛选机制，提高了直接模型预测控制的运算效率.

3）利用扇区相邻的电压矢量合成参考电压矢量，并附加作用时间的总和与比值约束条件，压缩或延长电压矢量的作用时间，使其在控制周期的合理范围内，确保了合成电压矢量的有效性. 实验结果的对比分析表明了所提方法具有比传统方法更好的稳态性能和动态性能.

图9突加负载实验结果

Fig.9Experimental results of step change in load torque

图1三相两电平逆变器驱动永磁同步电机拓扑

Fig.1Topology of permanent magnet synchronous motor driven by three-phase two-level inverter

下载: 全尺寸图片

图2直接模型预测控制方案

Fig.2Direct model predictive control scheme

下载: 全尺寸图片

图3直接模型预测控制电压矢量占空比优化策略

Fig.3Voltage vector duty cycle optimization strategy for direct model predictive control

下载: 全尺寸图片

图4参考电压矢量所在扇区的划分示意图

Fig.4Schematic diagram of sector division where reference voltage vector is located

下载: 全尺寸图片

图5候选电压矢量合成图

Fig.5Candidate voltage vector synthesis diagram

下载: 全尺寸图片

图6永磁同步电机对拖实验平台

Fig.6Permanent magnet synchronous motor experimental platform

下载: 全尺寸图片

图7稳态实验结果

Fig.7Steady state experimental results

下载: 全尺寸图片

图8速度阶跃实验结果

Fig.8Experimental results of step change in speed

下载: 全尺寸图片

图9突加负载实验结果

Fig.9Experimental results of step change in load torque

下载: 全尺寸图片

表13种方法的稳态实验结果对比

Table1Comparison of steady-state experimental results of the three methods

下载: 全尺寸图片

表23种方法的动态实验结果对比

Table2Comparison of dynamic experimental results of the three methods

下载: 全尺寸图片

图1三相两电平逆变器驱动永磁同步电机拓扑

Fig.1Topology of permanent magnet synchronous motor driven by three-phase two-level inverter

图2直接模型预测控制方案

Fig.2Direct model predictive control scheme

图3直接模型预测控制电压矢量占空比优化策略

Fig.3Voltage vector duty cycle optimization strategy for direct model predictive control

图4参考电压矢量所在扇区的划分示意图

Fig.4Schematic diagram of sector division where reference voltage vector is located

图5候选电压矢量合成图

Fig.5Candidate voltage vector synthesis diagram

图6永磁同步电机对拖实验平台

Fig.6Permanent magnet synchronous motor experimental platform

图7稳态实验结果

Fig.7Steady state experimental results

图8速度阶跃实验结果

Fig.8Experimental results of step change in speed

图9突加负载实验结果

Fig.9Experimental results of step change in load torque

表13种方法的稳态实验结果对比

Table1Comparison of steady-state experimental results of the three methods

表23种方法的动态实验结果对比

Table2Comparison of dynamic experimental results of the three methods

图1三相两电平逆变器驱动永磁同步电机拓扑

Fig.1Topology of permanent magnet synchronous motor driven by three-phase two-level inverter

图2直接模型预测控制方案

Fig.2Direct model predictive control scheme

图3直接模型预测控制电压矢量占空比优化策略

Fig.3Voltage vector duty cycle optimization strategy for direct model predictive control

图4参考电压矢量所在扇区的划分示意图

Fig.4Schematic diagram of sector division where reference voltage vector is located

图5候选电压矢量合成图

Fig.5Candidate voltage vector synthesis diagram

图6永磁同步电机对拖实验平台

Fig.6Permanent magnet synchronous motor experimental platform

图7稳态实验结果

Fig.7Steady state experimental results

图8速度阶跃实验结果

Fig.8Experimental results of step change in speed

图9突加负载实验结果

Fig.9Experimental results of step change in load torque

表13种方法的稳态实验结果对比

Table1Comparison of steady-state experimental results of the three methods

表23种方法的动态实验结果对比

Table2Comparison of dynamic experimental results of the three methods

ZHANG Y, YANG H. Model predictive torque control of induction motor drives with optimal duty cycle control. IEEE Transactions on Power Electronics,2014,29(12):6593-6603.

SUN Jian, ZHANG Xin. Three phase vector dual selection predictive torque control for permanent magnet synchronous motors. Proceedings of the CSU-EPSA,2024,36(9):22-30.(孙坚, 张馨. 永磁同步电机三相矢量双选取预测转矩控制. 电力系统及其自动化学报,2024,36(9):22-30.)

XIA C, WANG S, WANG Z,et al. Direct torque control for VSIPMSMs using four-dimensional switching-table. IEEE Transactions on Power Electronics,2016,31(8):5774-5785.

LIU Zhongyong, FAN Tao, HE Guolin,et al. Research on explicit model predictive control algorithm for high-performance permanent magnet synchronous motors. Transactions of China Electrotechnical Society,2023,38(22):6039-6058.(刘忠永, 范涛, 何国林, 等. 高性能永磁同步电机显式模型预测控制算法研究. 电工技术学报,2023,38(22):6039-6058.)

WANG F, XIE H, CHEN Q,et al. Parallel predictive torque control for induction machines without weighting factors. IEEE Transactions on Power Electronics,2020,35(2):1779-1788.

MUDDINENI V P, SANDEPUDI S R, BONALA A K. Finite control set predictive torque control for induction motor drive with simplified weighting factor selection using TOPSIS method. IET Electric Power Applications,2017,11(5):749-760.

ZHANG Pinghua, FAN Huiyan, WANG Shuang. Model predictive torque control without cost function for improved dual three-phase permanent magnet synchronous motor. Electric Machines & Control Application,2024,51(5):30-38.(张平化, 范慧妍, 王爽. 一种改进的双三相永磁同步电机无价值函数模型预测转矩控制. 电机与控制应用,2024,51(5):30-38.)

WANG Anpeng, HUANG Xuzhen, LI Liyi,et al. Multi-step model predictive current control method with variable weighting factor for permanent magnet linear synchronous motors. Proceedings of the CSEE,2022,42(22):8332-8343.(王安鹏, 黄旭珍, 李立毅, 等. 永磁直线同步电机的变权重系数多步模型预测电流控制方法. 中国电机工程学报,2022,42(22):8332-8343.)

ESWAR K M R, KUMAR K V P, KUMAR T V. Modified predictive torque and flux control for open end winding induction motor drive based on ranking method. IET Electric Power Applications,2018,12(4):463-473.

YAO Xuliang, HUANG Chengqi, WANG Jingfang,et al. Dual-vector model predictive current control with parameter identification function for permanent magnet synchronous motors. Proceedings of the CSEE,2023,43(23):9319-9330.(姚绪梁, 黄乘齐, 王景芳, 等. 具有参数辨识功能的永磁同步电机双矢量模型预测电流控制. 中国电机工程学报,2023,43(23):9319-9330.)

ZHANG Zhenrui, LIU Yancheng, CHEN Jiulin,et al. Amplitude control set model predictive control strategy for permanent magnet synchronous motor. Transactions of China Electrotechnical Society,2022,37(23):6126-6134.(张珍睿, 刘彦呈, 陈九霖, 等. 永磁同步电机幅值控制集模型预测控制策略. 电工技术学报,2022,37(23):6126-6134.)

LI X, XUE Z, YAN X,et al. Low-complexity multi-vector-based model predictive torque control for PMSM with voltage preselection. IEEE Transactions on Power Electronics,2021,36(10):11726-11738.

DASTJERDI R S, ABBASIAN M A, SAGHAFI H,et al. Performance improvement of permanent-magnet synchronous motor using a new deadbeat-direct current controller. IEEE Transactions on Power Electronics,2019,34(4):3530-3543.

ZHOU Z, XIA C, YAN Y,et al. Torque ripple minimization of predictive torque control for PMSM with extended control set. IEEE Transactions on Industrial Electronics,2017,64(9):6930-6939.

YANG Kuangbiao, MA Jingzi, YE Yunchong,et al. Predictive torque control of permanent magnet synchronous motor model based on virtual voltage vector. Small & Special Electrical Machines,2024,52(8):48-52.(杨狂彪, 马静子, 叶云翀, 等. 基于虚拟电压矢量的永磁同步电机模型预测转矩控制. 微特电机,2024,52(8):48-52.)

KANG S, SOH J, KIM R. Symmetrical three-vector-based model predictive control with deadbeat solution for IPMSM in rotating reference frame. IEEE Transactions on Industrial Electronics,2020,67(1):159-168.

ROJAS C A, RODRIGUEZ J. Predictive torque and flux control without weighting factors. IEEE Transactions on Industrial Electronics,2013,60(2):681-690.

HUANG W, HUA W, YIN F,et al. Model predictive thrust force control of a linear flux-switching permanent magnet machine with voltage vectors selection and synthesis. IEEE Transactions on Industrial Electronics,2019,66(6):4956-4967.

ZHANG X, HOU B. Double vectors model predictive torque control without weighting factor based on voltage tracking error. IEEE Transactions on Power Electronics,2018,33(3):2368-2380.

XIAO M, SHI T, YAN Y,et al. Predictive torque control of permanent magnet synchronous motors using flux vector. IEEE Transactions on Industry Applications,2018,54(5):4437-4446.