欢迎访问《控制理论与应用》期刊网站！

集中训练分布执行下的多智能体强化学习综述

doi: 10.7641/CTA.2025.50009

李岳珩¹ ，谢广明^1,2

1. 北京大学先进制造与机器人学院, 北京 100871

2. 北京大学人工智能研究院, 北京 100871

基金项目: 国家自然科学基金项目(U22A2062, U23B2037), 北京市自然科学基金项目(L222084, 3242003)资助

详细信息

作者简介

李岳珩博士研究生,目前研究方向为强化学习与多智能体强化学习,E-mail: liyueheng@pku.edu.cn;

谢广明教授,博士生导师,目前研究方向为仿生机器人、机器人集群与学习控制,E-mail: xiegming@pku.edu.cn.

通信作者

谢广明，E-mail: xiegming@pku.edu.cn;Tel.:+8610-62754083.

Review of multi-agent reinforcement learning under centralized training with decentralized execution

LI Yue-heng¹ ， XIE Guang-ming^1,2

1. School of Advanced Manufacturing and Robotics, Peking University, Beijing 100871 , China

2. Institute of Artificial Intelligence, Peking University, Beijing 100871 , China

Funds: Supported by the National Natural Science Foundation of China (U22A2062, U23B2037) and the Beijing Natural Science Foundation (L222084, 3242003).

摘要

近年来, 多智能体强化学习(MARL)因其在解决实际问题上的巨大潜力而逐渐成为研究的热点. 在复杂的多智能体系统中, 集中式训练与分布式执行(CTDE)框架被广泛应用. CTDE通过集中训练的方式缓解了多智能体强化学习中的非平稳性问题, 但也因此带来了新的挑战, 特别是在训练过程中需要处理所有智能体的信息, 尤其是随着智能体数量增加而呈指数级增长的联合动作空间. 本文对CTDE框架下的多智能体强化学习算法及其发展进行了选择性的回顾, 重点探讨了两大类算法: 值函数分解方法和策略梯度方法. 本文总结了这些算法在处理联合动作空间复杂性、非平稳性问题以及估计误差方面的表现, 并提出了一些新的视角和思路, 旨在为该领域的研究人员提供更深入的理解和未来研究的指导.

关键词

多智能体强化学习 / 集中式训练分布式执行 / 值函数分解 / 强化学习

Abstract

In recent years, multi-agent reinforcement learning (MARL) has gained significant attention due to its potential in solving complex real-world problems. The centralized training with decentralized execution (CTDE) framework has been widely adopted in complex multi-agent systems. CTDE alleviates the non-stationarity problem in MARL by utilizing centralized training, but it also introduces new challenges, particularly in handling the information of all agents during training, especially the exponentially growing joint action space as the number of agents increases. This paper provides a selective review of the algorithms and developments in cooperative multi-agent reinforcement learning within the CTDE framework, focusing on two main approaches: Value function factorization methods and policy-based methods. This paper summarizes the performance of these algorithms in addressing the complexity of joint action spaces, non-stationarity, and estimation errors. It also proposes new perspectives and ideas, aiming to provide researchers in the field with deeper insights and guidance for future studies.

Keywords

multi-agent reinforcement learning / centralized training with decentralized execution / value factorization / reinforcement learning

1 引言 2 背景知识 2.1 问题阐述 2.2 基于值函数的强化学习方法 2.3 基于策略的强化学习方法 3 值函数分解方法 3.1 线性值函数分解 3.2 单调值函数分解 3.3 具有完全表达能力的方法 4 基于策略的方法 4.1 单智能体RL的直接扩展 4.2 与值函数分解方法的结合 5 进一步讨论 5.1 外推误差 5.2 现有方法的进一步改进 6 结束语

1 引言

近年来，深度学习技术和计算资源的飞速发展推动了人工智能领域的重大突破，不仅为诸多实际问题提供了解决方案，还逐步应对了更为复杂和具有挑战性的任务. 深度学习的成功应用推动了传统领域的进展，并加速了新兴领域的发展.

在实际应用中，许多问题可以建模为多智能体系统（multi-agent system，MAS）^[1]，其中多个智能体通过协作共同完成团队目标，从而提升整体系统效益. 合作多智能体强化学习（multi-agent reinforcement learning，MARL）^[2-3] 作为一种具有巨大潜力的解决方案，已在自动驾驶 ^[4]、智能交通管理 ^[5]、机器人集群协作 ^[6-7] 等领域展示了其有效性.

然而，随着应用场景复杂度的增加，特别是在系统规模扩展时，MARL面临着显著挑战. 具体而言，随着智能体数量的增加，联合动作空间的维度呈指数级增长，极大地考验了算法的可扩展性（scalability）. 此外，由于智能体之间通信受限，许多多智能体系统中的智能体需要基于自身局部信息进行分布式决策，这也增加了协作的难度.

为应对这些挑战，集中式训练与分布式执行（centralized training with decentralized execution，CTDE）框架 ^[8-9] 被广泛采用. 该框架充分利用了强化学习训练与执行的分离特性. 在训练阶段，所有智能体的信息集中处理，使每个智能体能够访问其他智能体的动作、观测及全局信息; 而在执行阶段，每个智能体根据自身的局部观测独立决策，无需依赖其他智能体的通信. 该结构既能在训练过程中充分利用共享信息，又能在执行阶段保持分布式决策.

CTDE框架不仅有效利用全局信息，还成功解决了多智能体强化学习中的非平稳性问题. 在没有集中训练的情况下，每个智能体只能将其他智能体视为环境的一部分，于是智能体策略的不断变化会导致环境的非平稳性，从而影响训练的稳定性. CTDE通过集中训练确保所有智能体的策略被同时考虑，使其在相对稳定的环境中学习. 然而，随着智能体数量的增加，联合动作空间的指数级增长使得算法在集中训练阶段面临更大的挑战，尤其是在值函数估计的准确性方面.

目前，在CTDE框架下表现出色的算法，大多能够较为成功地应对联合动作空间的复杂性. 一类是值函数分解方法 ^[10-11]，通过分解近似的动作值函数，减少了需要估计的联合动作空间，从而提高了学习效率，能够更好地逼近最优策略; 另一类是传统的策略梯度方法 ^[12-13]，通过估计状态值函数来更新每个智能体的策略，避免了直接处理联合动作空间的复杂性.

然而，现有研究缺乏一个系统的视角来全面评估 CTDE框架下的MARL算法，且算法的实际表现往往与理论性质不一致. 理论上的改进有时反而导致实际性能的下降. 从统计数据 ^[14]（图1–2）来看，近年来该领域的方法呈现出下降趋势，而最常用的方法，尤其是在2023和2024年，仍然是2018年和2021年提出的经典方法QMIX ^[11] 和多智能体近端策略优化（multi-agent proximal policy optimization，MAPPO）^[13] . 这表明该领域的发展可能已接近瓶颈期，亟需新的视角和研究方向. 鉴于此，本文回顾了CTDE框架下的主要MARL算法，并提出新的分析视角，以更深入地理解这些算法的有效性. 本文的目标是为读者提供全面深入的理解，并为后续的算法改进和研究提供启示.

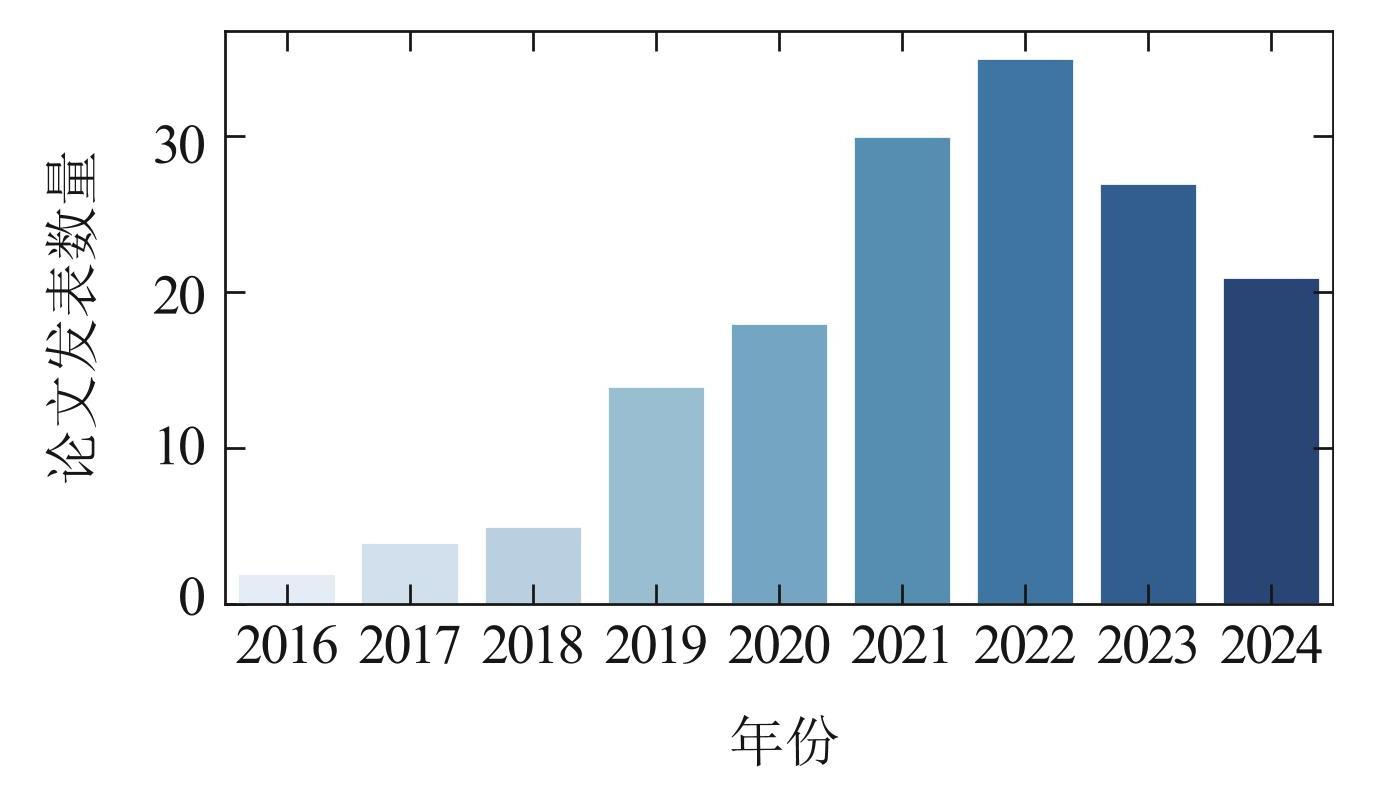
图1合作多智能体强化学习顶会论文近年发表情况

Fig.1Top conference publication status of collaborative MARL papers in recent years

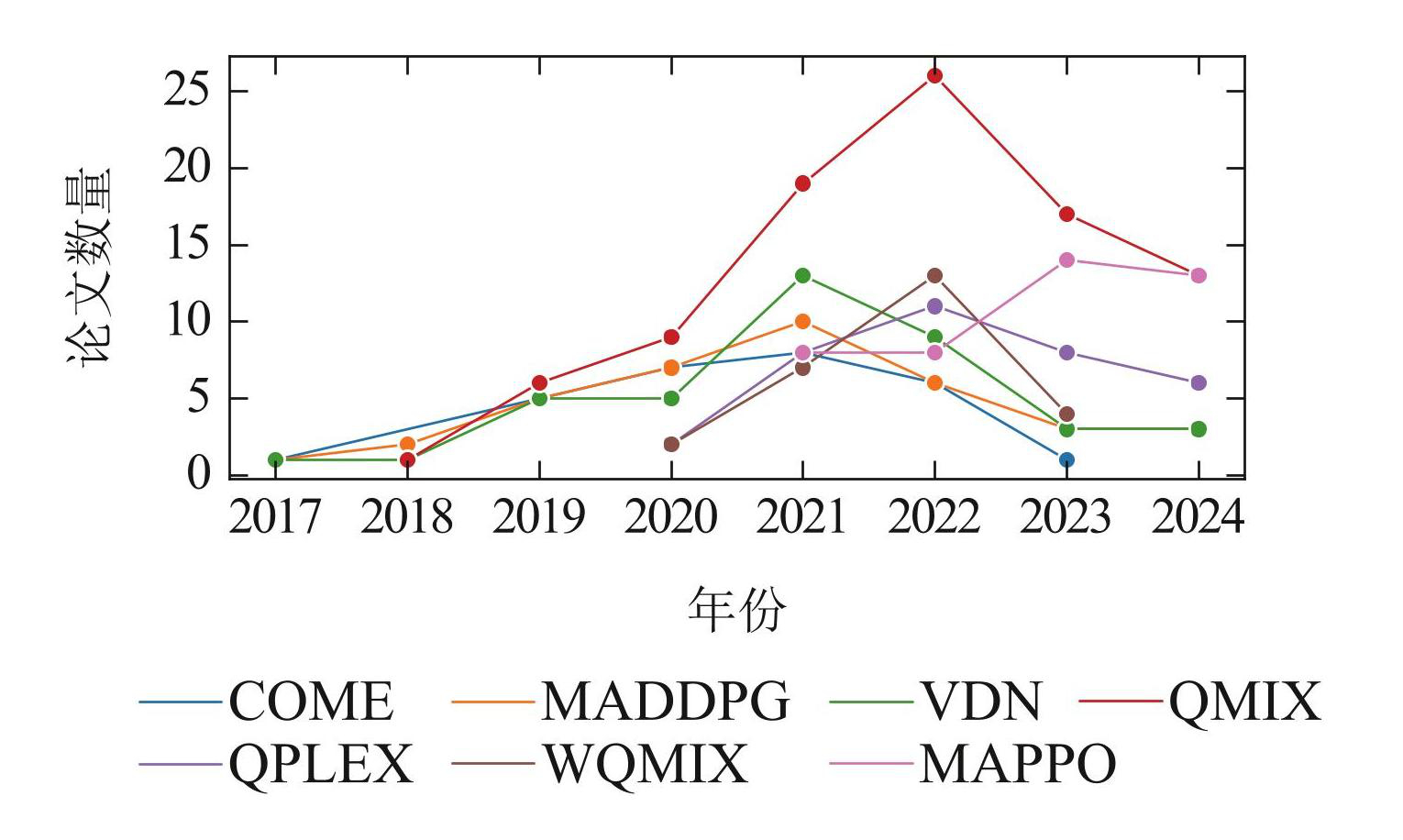
图2过去几年论文中算法出现次数的对比

Fig.2Comparison of the number of algorithm occurrences in the past few years

鉴于CTDE框架下的MARL算法种类繁多，本文将重点讨论那些对理解该领域尤为重要的算法（表1），而非涵盖所有相关算法. 具体而言，第2节简要介绍 MARL的背景设定以及强化学习（reinforcement learning，RL）^[15] 的基础知识; 第3节和第4节分别介绍基于值的和基于策略的MARL算法; 第5节对相关算法进行了讨论，提出新的视角和可能分析框架; 第6节总结了全文工作.

表1代表性算法

Table1Representative algorithms

2 背景知识

本节简要介绍有关MARL的背景设定及基础知识，以便后续算法的介绍. 有关CTDE下的MARL算法的介绍不会在本节直接涉及，而是被分布到后续章节中.

2.1 问题阐述

合作MARL任务通常被建模为部分可观测马尔可夫决策过程（partial observable Marcov decision process，Dec-POMDP）^[23]，其可由元组

⟨ N ， S ， A ， r ， P ， O ， Z ， γ ⟩

描述. 其中:

N

代表智能体的集合，

S

代表状态的集合，

A

代表每个智能体动作的集合，r是奖励函数，P是环境转移概率函数， Z是每个智能体由观测函数 O生成的部分观测集合，γ是折扣因子. 在每个时间步，每个智能体i ∈

N

首先根据其观测函数

O

（s; i）接收一个局部观察o_i ∈ Z; 然后，每个智能体i根据其自身的策略π_i，基于动作观测历史τ_i ∈（Z ×

A

）^∗选择一个执行动作a_i∈

A

. 所有智能体执行动作后形成一个联合动作a，使得环境根据状态转移

P (s^{'} ∣ s ， a)

从状态s 转移到下一个状态s′; 最后，所有智能体都会收到一个共享的奖励r. MARL 的目标是寻找一个联合策略 π =

\prod_{i = 1}^{n} π_{i}

使得累计期望回报最大，其目标函数可定义为

V^{π} (s) = E [\sum_{t = 0}^{\infty} γ^{t} r_{t} ∣ s_{0} = s, π],

(1)

因此，联合动作值函数可相应地定义为

Q^{π} (s, a) = r + E_{s^{'} \sim P (\cdot ∣ s, a)} [V^{π} (s)]

(2)

由于本文考虑CTDE框架 ^[8-9] 下的MARL算法，在集中训练的过程中，假设可以获取状态s以及所有智能体的观测τ和动作a. 因此，MARL算法可以直接对联合（动作）值函数进行估计，并利用该值函数去优化基于部分观测的策略π_i（·|τ_i），从而满足分布式执行的需求. 为了符号的简洁性，假设状态s包含了所有智能体的观测τ，故后文的全局信息均由s表示.

2.2 基于值函数的强化学习方法

本小节首先回顾单智能体下的值函数方法. 此类方法通常使用贝尔曼最优方程迭代优化动作值函数 Q，即Q函数

Q (s, a) = \sum_{s^{'}} p (s^{'}, r ∣ s, a) [r + γ \underset{a^{'}}{m a x} Q (s^{'}, a^{'})],

(3)

基于该方程迭代即为Q-learning方法 ^[24] .

然而，当面临大型或连续状态空间时，通常需要使用神经网络（其参数记为θ）来近似估计Q函数的值. 在这种情况下，深度Q网络（deep Q network，DQN）^[25] 将优化目标转化为以下损失函数:

L (θ) = E_{(s, a, r, s^{'}) \sim D} [(Q (s, a; θ) - y)^{2}]

(4)

其中:

y = r + γ \underset{a^{'}}{m a x} Q (s^{'} ， a^{'}; θ^{'}) ， D

为经验回放池. 函数

Q (\cdot; θ^{'})

为延迟更新的目标网络，其参数θ′以固定延迟的方式复制参数θ，从而确保目标网络的稳定性.

将单智能体下的基于值函数的RL方法扩展到MARL中，一个直接的方法是对每个智能体分别使用单智能体 RL方法. 例如，在独立 Q学习（independent Qlearning，IQL）^[26-27] 中，算法针对每个智能体学习一个独立的Q 函数Q_i（τ_i，a_i; θ_i），并分别使用DQN进行更新，即

L (θ_{i}) = E_{(τ_{i}, a_{i}, r, τ_{i}^{'}) \sim D} [{(Q_{i} (τ_{i}, a_{i}; θ_{i}) - y_{i})}^{2}]

(5)

需要注意的是，由于在Dec-POMDP中通常需要处理历史轨迹，Q函数往往会采用循环神经网络（recurrent neural network，RNN）进行训练 ^[27] . 为了简洁起见，本文不会涉及RNN的建模与训练过程，有关内容可参考文献 ^[27-28] .

2.3 基于策略的强化学习方法

本小节回顾单智能体下的基于策略的强化学习方法. 策略梯度方法可以视为求解如下优化问题:

\underset{π}{m a x} V^{π} (s_{0}),

(6)

这类方法基于策略梯度定理 ^[15] 进行策略迭代，包含策略评估和策略提升两个阶段. 在策略评估阶段，算法拟合值函数V ^π（s）或者Q^π（s， a）以评估当前策略π下能取得的期望回报. 在策略提升阶段，算法基于值函数对当前策略的目标函数做梯度上升，从而改进策略. 例如，对于随机策略，策略梯度可以写为如下形式:

\nabla_{θ} J (θ) = E_{s \sim d_{ρ}^{π}} E_{a \sim π} [\nabla_{θ} l o g π_{θ} (a ∣ s) Q^{π_{θ}} (s, a)],

(7)

其中

d_{ρ}^{π} = E_{s_{0} \sim ρ} [\sum_{t = 0}^{\infty} P r (s_{t} = s ∣ s_{0})]

为给定初始状态分布ρ下状态访问分布. 在后文中，随机策略梯度的期望简写为E_π.

对于确定性策略µ_θ（s），其对应确定性策略梯度（deterministic policy gradient，DPG）^[29] 为

\nabla_{θ} J (θ) = E_{s \sim D} [{\nabla_{θ} μ_{θ} (s) \nabla_{a} Q^{μ_{θ}} (s, a)|}_{a = μ (s)}]

(8)

其中D是经验回放池.

类似于基于值的强化学习方法，将基于策略的强化学习方法扩展为MARL方法的一种直接方式，是对每个智能体分别应用单智能体的强化学习方法. 例如，针对每个智能体使用随机策略梯度（7）对应的优势演员–评论家（advantage actor-critic，A2C）算法和近端策略优化（proximal policy optimization，PPO）算法 ^[30]，或确定性策略梯度（8）对应的深度确定性策略梯度算法（deep deterministic policy gradient，DDPG）^[31]，这些内容不再展开讨论，有关内容可参考文献 ^[18，32] .

3 值函数分解方法

本节介绍值函数分解系列方法，这类方法基于Q 函数的迭代求解来获得最优策略. 然而，若希望在CTDE框架下应用基于值的强化学习方法，单独估计一个全局Q函数Q_tot（s，a）来评估状态s下联合动作a是不够的，因为该方法无法支持分布式决策. 因此，在集中训练阶段，需要为每个智能体学习一个局部 Q 函数 Q_i（τ_i，a_i），该函数仅评估智能体在其局部观测τ_i下动作a_i的效用，并用于执行时的动作选择.

在本文中，Q_tot被称为全局Q函数， Q_i被称为局部效用函数. 由于全局Q函数的定义通过贝尔曼最优方程已经明确，而局部效用函数的定义是不明确的，如何定义并高效地学习局部效用函数Q_i，使得基于Q_i的策略仍具有最优性，正是值函数分解方法的核心问题.

为了确保每个智能体基于自身效用函数选择的动作在全局来看也是最优的，局部效用函数 Q_i和全局 Q 函数Q_tot必须满足一定的约束，称为IGM（individual-global-max）约束 ^[16] . 具体地，IGM要求

\arg max_{a} Q_{tot} (s, a) = \{\begin{matrix} \arg max_{a_{1}} Q_{1} (τ_{1}, a_{1}), \\ ⋮ \\ \arg max_{a_{n}} Q_{n} (τ_{n}, a_{n}), \end{matrix}

(9)

顾名思义，IGM约束要求当全局Q函数选择最大值时，所有局部效用函数也必须选择各自的最大值. 换句话说，由全局Q函数选择的联合动作a必须与每个局部效用函数选择的动作a_i一致. 因此，IGM确保了智能体在分布式执行时选择的动作也是最优的.

对于IGM约束，有几个关键问题需要讨论. 首先，IGM约束是一个较为宽松的条件，因其仅要求最优动作的一致性. 而对于非最优动作，理论上局部效用函数的值可以是任意低于

\underset{a_{i}}{m a x} Q_{i} (τ_{i} ， a_{i})

的数值. 因此，单凭IGM约束无法完全确定局部效用函数的具体形式，还需要引入其他约束来确定非最优动作对应的值. 其次，IGM所要求的最优动作在实际中往往难以精确达到. 直接对全局Q函数进行极值求解通常被认为是不可行的，因为这需要遍历整个联合动作空间. 因此，最优动作往往是通过局部效用函数间接获得的，而由于估计误差、模型误差等因素，得到的动作通常是次优的，进而会受到局部效用函数次优值的影响. 这也说明，虽然效用函数在非最优动作上的值理论上可以任意，但在实际应用中仍需谨慎设计，以尽可能反映真实值. 此外，一些常见的算法，如值分解网络（value decomposition network，VDN）^[10] 和QMIX ^[11]，即使不考虑估计误差，实际上也未严格满足IGM约束，因为它们的全局Q函数通常不满足贝尔曼最优方程. 这一点将在后续讨论中进一步展开.

接下来，本文将介绍几种具体的值函数分解主流算法. 需要注意的是，尽管一些早期的算法并未明确考虑如何在CTDE框架下处理联合动作空间及如何达成最优一致性（例如，VDN的提出主要是为了解决智能体信用分配的问题 ^[33]），但本文仍将以分解联合动作空间并实现最优一致性为核心视角，介绍这些方法的具体实现.

3.1 线性值函数分解

线性值函数分解方法源自VDN ^[10] 算法. 它将全局Q函数表示为局部效用函数的线性组合，因其简洁性而被广泛应用于后续算法中，甚至作为基线算法使用.

作为最早提出的值函数分解方法，VDN的基本思想非常直观. 具体而言，它假设全局Q 函数可以表示为局部效用函数之和，即

Q_{t o t} (s, a) = \sum_{i = 1}^{n} Q_{i} (τ_{i}, a_{i}),

(10)

因此，在VDN的值函数迭代更新中，只需将该表达式带入DQN的更新公式（式（4）），就能直接对每个局部效用函数进行更新

L (θ) = E_{D} [{(\sum_{i = 1}^{n} Q_{i} (τ_{i}, a_{i}) - y_{V D N})}^{2}]

(11)

其中

y_{V D N} = r + γ \sum_{i = 1}^{n} \underset{a_{i}^{'}}{m a x} Q_{i} (τ_{i}^{'} ， a_{i}^{'}) .

接下来，一个关键问题是验证VDN的分解是否满足最优一致性. 由于式（10）线性组合的性质，容易得出结论: 当全局Q函数取最大值时，局部效用函数Q_i也会在对应的动作上取最大值. 因此，由局部效用函数所选择的动作在全局视角下也是最优的. 然而，尽管 VDN满足最优一致性，它通常不满足IGM约束. 这是因为通过VDN定义的全局Q函数通常不满足贝尔曼最优方程，这意味着基于Q_tot得到的最优策略未必是任务的实际最优策略. 只有在特殊情况下，当贝尔曼最优方程恰好可以通过局部效用函数的线性分解来表示时，VDN得到的策略才是最优的. 否则，VDN得到的策略往往是次优的.

这种问题通常被称为值函数的表达能力（expressive ability）问题，其表现在于VDN对Q_tot的形式进行了过强的约束，从而限制了其表达能力，无法满足贝尔曼最优方程. 尽管如此，由于VDN 方法简单易用，特别是在任务合作性质不复杂、每个智能体奖励相对独立时，VDN仍然是一种有效的选择.

值得注意的是，正如式（10）所示，VDN无法利用额外的全局信息s. 它仅依赖于每个智能体的局部效用函数Q_i（τ_i， a_i），其中τ_i是智能体i的局部观测. 若希望利用全局信息，VDN也可以被直接地扩展为考虑全局信息的版本. 具体而言，可以引入基于全局信息的权重w_i（s）和偏置b（s），考虑如下线性组合:

Q_{t o t} (s, a) = \sum_{i = 1}^{n} w_{i} (s) Q_{i} (τ_{i}, a_{i}) + b (s),

(12)

此处的权重和偏执可以直接由一个输入为s的神经网络输出，也能通过更加复杂注意力机制（attention）^[34] 去提升效果，例如Qatten ^[35] 算法，此处不再详细讨论.

这种扩展能够利用全局信息，并且在满足w_i（s）>0的条件下，同样能确保最优一致性. 通过这种方法，线性分解的表达能力得到了增强，这也是VDN被使用较多的版本. 后文中，这种扩展后的形式统一称为“线性分解”. 需要注意的是，尽管引入了全局信息的权重和偏置，该分解仍然是一个线性模型，因此在许多任务中，它仍然无法保证最优性. 此外，线性分解也无法进一步扩展为基于动作的权重 w_i（s，a_i）和偏置 b（s，a_i），因为这会破坏最优一致性，导致结果发散. 更多关于线性分解的理论可参考文献 ^[36-37] .

3.2 单调值函数分解

如上文所述，由于线性分解的约束过强，其表达能力受到了较大的限制，因此后续的算法对这一问题进行了改进. 本节介绍著名的 QMIX ^[11] 算法，它是目前应用最广泛且综合表现最好的值函数分解算法之一 ^[38-39].

QMIX指出，VDN 所提出的全局Q 函数的线性分解约束过强，可以用单调性约束来替代. 具体而言，QMIX引入了以下单调性约束:

\frac{\partial Q_{t o t} (s, a)}{\partial Q_{i} (τ_{i}, a_{i})} ⩾ 0

(13)

该约束实际上隐式地给出了一个函数表达式

Q_{t o t} (s, a) = f (s, Q_{1} (τ_{1}, a_{1}), \dots, Q_{n} (τ_{n}, a_{n})),

(14)

其中函数f 对每个局部效用函数Q_i的偏导数大于等于0.

可以看出，线性分解都为上述形式的特殊情况，对应于线性的函数f. 而QMIX的做法是直接对单调函数f进行参数化，将其视为一个输入为局部效用函数、输出为全局Q函数的神经网络，其中网络的权重和偏置由一个输入为状态 s 的超网络（hypernetwork）^[40] 生成. 为了确保f的单调性，QMIX在超网络生成的权重上施加了绝对值限制，从而保证了函数对所有输入的偏导数是非负的.

QMIX最终将该表达式代入DQN的损失函数，并在训练过程中同时优化函数f和局部效用函数Q_i，即

L (θ) = E_{D} {[f (s, Q_{1} (τ_{1}, a_{1}), \dots, Q_{n} (τ_{n}, a_{n})) - y_{Q M I X})}^{2}]

(15)

其中

y_{Q M I X} = r + γ \underset{a^{'}}{m a x} f (s^{'} ， Q_{1} ， \dots ， Q_{n}) .

从IGM的角度来看，QMIX无疑满足最优一致性: 由于其单调性约束，全局Q 函数取最大值时，所有局部效用函数也会达到最大值. 因此，QMIX保证了智能体在执行时选择的动作与全局最优动作一致. 尽管 QMIX的约束相比于线性分解更弱，但它仍然不具有完全表达能力. 例如，非单调矩阵无法被单调函数正确拟合 ^[41] . 因此，QMIX在许多情况下仍无法满足贝尔曼最优方程，导致其收敛到次优解.

一些基于QMIX的后续改进方法（如WQMIX（weighted-QMIX））尝试解决这一问题. WQMIX ^[42] 的核心思想是，虽然QMIX无法满足贝尔曼最优方程，但能让其最优动作对应的 Q 值满足贝尔曼最优方程. 为此，WQMIX引入了动态权重w（s，a），分别作用于最优和非最优动作. 通过提高最优动作的权重，在理论上，最优动作的值函数将更接近贝尔曼最优方程，从而使得 WQMIX 更容易收敛到最优解. 然而，实际训练过程中仍然需要通过估计的值函数来确定最优动作，误差依然存在. 这使得WQMIX只能在简单的任务上领先 QMIX，且由于其复杂性导致后续工作仍倾向于直接使用QMIX.

3.3 具有完全表达能力的方法

本小节介绍具有完全表达能力的方法，即分解后的值函数仍能够完全表达任意全局Q函数. 由于完全表达能力需要能够拟合从联合状态–动作空间到实数的任意映射，因此这类方法不可避免地需要直接考虑联合动作a，这实际上带来了许多问题，这些问题将在第5节进一步探讨.

最早提出的具有完全表达能力的算法是 QTRAN ^[16] . QTRAN的方法并未直接将全局Q 函数与局部效用函数之间的关系参数化，而是通过一个约束条件来表示这一关系

\sum_{i = 1}^{n} Q_{i} (τ_{i}, a_{i}) - Q_{t o t} (s, a) + V (s) = \{\begin{matrix} 0, a = \bar{a}, (16 a) \\ ⩾ 0, a \neq \bar{a}, (16 b) \end{matrix}

(16)

其中

\bar{a}

是由所有局部效用函数选出来的最优动作的集合，以及

V (s) = \underset{a}{m a x} Q_{t o t} (s, a) - \sum_{i = 1}^{n} Q_{i} (τ_{i}, {\bar{a}}_{i})

(17)

为状态值函数.

QTRAN提出的约束形式直接反映了IGM的思想: 只需保证最优动作一致性（式（16a）），非最优动作的值函数可以为小于最优值函数的任意值（式（16b））. 由于 QTRAN没有给出全局Q函数与局部效用函数的显式关系，在训练时，其需要分别对全局Q函数和局部效用函数进行拟合与更新. 全局Q函数的训练可以直接被视为单智能体RL，通过DQN的损失函数进行. 对于局部效用函数，QTRAN引入了以下两个损失函数，分别对最优和非最优动作对应的函数值进行约束:

L_{o p t} = {(Q_{t o t} (s, a) - \sum_{i = 1}^{n} Q_{i} (τ_{i}, a_{i}) + V (s))}^{2},

(18)

L_{n o p t} = (m i n [Q_{t o t} (s, a) - {\sum_{i = 1}^{n} Q_{i} (τ_{i}, a_{i}) + V (s), 0])}^{2},

(19)

由于全局 Q 函数没有额外约束，QTRAN的Q_tot可以收敛到最优值，从而使局部效用函数也收敛到最优.

QTRAN尽管在理论上具有良好的性质，但在实际使用中存在许多问题. 例如，由于QTRAN的约束是损失函数形式，它并不能保证在训练过程中约束条件一定满足; 此外，直接学习全局Q函数需要在联合动作空间上进行拟合，这使得其收敛困难. 而在Q_tot尚未收敛时，QTRAN对局部效用函数的约束可能使其拟合存在较大误差，尤其是当约束对非最优值函数的限制较弱时. 虽然QTRAN论文中提到了这个问题，并提出了QTRAN-alt来加强对非最优值的约束，但总体而言QTRAN在复杂任务中表现仍然不佳.

QTRAN 的后续的改进 QTRAN++ ^[43] 对QTRAN 中的非最优动作做了更强的约束. 此外，在学习全局 Q函数时，QTRAN++使用了QMIX的结构来提升性能. 虽然QTRAN++在复杂任务上的表现相比QTRAN有了很大提升，但由于其算法的复杂性，后续较少有人使用.

另一个具有完全表达能力的算法是QPLEX ^[17]，其表达式为

Q_{tot} (s, a) = \sum_{i = 1}^{n} Q_{i} (s, a_{i}) + \sum_{i = 1}^{n} (λ_{i} (s, a) - 1) A_{i} (s, a_{i}),

(20)

其中

A_{i} (s ， a_{i}) = Q_{i} (s ， a_{i}) - \underset{a_{i}}{m a x} Q_{i} (s ， a_{i}) .

该表达式中 Q_i是关于全局状态s的是，因为 QPLEX将局部效用函数先用注意力机制做了线性变换 Q_i（s，a_i）=w_i（s）Q_i（τ_i，a_i）+ b_i（s）.

QPLEX通过约束λ_i（s，a）>0保证了Q_tot对Q_i（s，a_i）的单调性. 此外，由于其线性变换也保持了单调性，因此当全局Q函数Q_tot达到最大值时，所有局部效用函数Q_i（τ_i， a_i）也会达到最大值，从而，确保了最优动作的一致性. QPLEX的完全表达能力体现在，其能拟合任意从联合状态–动作空间到实数的映射g（s，a）. 对于任意函数g，可以选择

λ_{i} (s, a) = \frac{g (s, a) - \underset{a}{m a x} g (s, a)}{n A_{i} (s, a_{i})},

(21)

从而确保λ_i（s，a）>0，并且满足

Q_{t o t} (s, a) = g (s, a) - \underset{a}{m a x} g (s, a) + \sum_{i = 1}^{n} \underset{a_{i}}{m a x} Q_{i} (s, a_{i}),

(22)

进一步，令

\sum_{i = 1}^{n} \underset{a_{i}}{m a x} Q_{i} (s ， a_{i}) = \underset{a}{m a x} g （ s ， a ） ，

即可得到 Q_tot（s，a）= g（s，a）.

这表明，对于任意的g存在λ_i和Q_i来满足该关系. 因此，QPLEX的分解能够满足贝尔曼最优方程，理论上能够收敛到最优解. 同时，由于QPLEX给出了全局 Q函数与局部效用函数的解析关系，其更新可以直接使用DQN进行端到端的训练，无需类似QTRAN的约束形式.

然而，从上述推导可以看出，QPLEX的强表达能力依赖于系数λ_i（s，a）. 由于该系数同样需要考虑联合动作空间，其拟合难度与全局Q函数相当，难以保证准确性. 为此，QPLEX采用了多头注意力机制来生成λ_i . 此外，QPLEX 通过停止一部分梯度传播，使得

\frac{\partial Q_{t o t} （ s ， a ）}{\partial Q_{i} (s ， a_{i})} = 1 ，

从而，提高了训练过程的稳定性. 得益于这些性质，QPLEX不仅能有效处理非单调的矩阵博弈任务，并且在复杂任务中表现也较好. 然而，QPLEX算法在实际使用中也存在不稳定性问题，其系数 λ_i的估计误差会不断累积引发数值不稳定，导致算法性能突然下降.

至此，本文已介绍了所有主要的值函数分解方法. 此后提出的算法大多未在理论上带来重大创新，也未在性能上显著提升，更多的是通过组合现有方法来解决一些细节性问题. 值得注意的是，尽管近年来值函数分解方法不断朝着最优性与表达能力的方向改进，一些后续的工作 ^[38-39] 在同样调优后的超参数设置下发现，目前表现最好的值函数分解算法仍然是QMIX. 这或许表明，表达能力并非在所有合作多智能体任务中都占主导地位，可能存在其他因素对算法表现的影响. 这一问题将在后续两节进一步探讨这一问题.

4 基于策略的方法

本节介绍在CTDE框架下常用的基于策略的方法. 与值函数分解方法不同，基于策略的方法可以分别处理值函数与策略，故大多数方法采用集中式的值函数和分布式的策略以利用CTDE框架. 这类方法通常不需要像值函数分解方法那样额外估计局部效用函数来获得分布式策略. 当然，许多算法也将值函数分解方法与基于策略的方法相结合，这些算法将在第4.2节中介绍.

4.1 单智能体RL的直接扩展

从单智能体RL到MARL的最直接扩展方法，是为每个智能体分别应用单智能体RL算法进行训练. 但这种方法无法利用全局信息，且由于智能体策略的不断变化，会导致非平稳性问题. 因此，CTDE框架下的算法通常通过集中式值函数将所有智能体的状态与动作纳入考量以解决这一问题.

例如，多智能体深度确定性策略梯度算法（multiagent DDPG，MADDPG）^[18] 通过集中式的Q函数扩展了确定性策略梯度（8），得到如下形式:

\nabla_{θ_{i}} J (θ_{i}) = E_{s, a_{- i} \sim D} [{\nabla_{θ_{i}} μ_{i} (s) \nabla_{a_{i}} Q^{μ_{θ}} (s, a_{i}, a_{- i})|}_{a_{i} = μ_{i} (s)}],

(23)

其中: µ_i为智能体i的策略; a₋_i代表除智能体i之外的所有智能体的联合动作. 与直接使用n个DDPG算法并行训练不同，MADDPG通过全局Q函数来评估所有智能体在状态s下的联合动作a，进而利用全局信息为智能体提供更准确的更新梯度. 同时，由于该训练方式同时考虑了所有智能体的策略，MADDPG 有效地解决了非平稳性问题.

类似的，反事实多智能体策略梯度（counterfactual multi-agent policy gradients，COMA）^[19] 通过集中式的 Q函数将随机策略梯度（7）拓展为如下形式:

\nabla_{θ} J (θ) = E_{π} [\sum_{i = 1}^{n} \nabla_{θ} l o g π_{i} (a_{i} ∣ τ_{i}) A_{i} (s, a)]

(24)

其中

A_{i} （ s ， a ） = Q (s ， a_{i} ， a_{- i}) - E_{π_{i}} [Q (s ， a_{i} ， a_{- i})]

为反事实优势函数，旨在用反事实的方式评估智能体i对团队的贡献. 与直接使用n个单智能体策略梯度方法相比，COMA不仅能利用全局信息解决非平稳性问题，还通过反事实优势函数有效地解决了智能体之间的信用分配问题. 多智能体信用分配是MARL中的一个重要问题 ^[33]，但由于篇幅限制，本文不做进一步探讨，有关论文可参考文献 ^[19，44-47] .

上述算法（MADDPG和COMA）是早期的CTDE框架下的MARL算法. 它们通过将单智能体算法中的值函数扩展为集中式来实现集中式训练. 虽然这一做法解决了非平稳性问题，且在一些简单环境中表现较好，但在更复杂的任务中（如SMAC（starcraft multi-agent challenge）^[48]），这两种算法的表现较差，有时甚至不如直接使用单智能体算法. 一个可能的原因是直接估计全局Q函数非常困难且误差较大，尽管全局信息能提供更准确的梯度，但由于估计误差，反而使梯度更加不准确.

同样作为单智能体RL方法的扩展，多智能体优势演员–评论家（multi-agent A2C，MAA2C）^[12] 和MAPPO ^[13] 在目前常见的环境中表现较好. 这两个方法也都遵循相同的思路，将值函数扩展为集中式值函数，从而提供更加准确的策略梯度.

例如，MAA2C的策略梯度同样基于单智能体随机策略梯度（7），表示如下:

\nabla_{θ} J (θ) = E_{π} [\sum_{i = 1}^{n} \nabla_{θ} l o g π_{i} (a_{i} ∣ τ_{i}) A^{π_{θ}} (s, a)],

(25)

该式与COMA类似，但其优势函数

A^{π_{θ}} （ s ， a ）

由

A^{π_{θ}} （ s ， a ）

= r + γV（s′）− V（s）计算. 与使用全局Q 函数的算法不同，MAA2C和MAPPO使用集中式的值函数 V（s），因此不涉及高维联合动作空间的估计. 这一差异使得MAA2C和 MAPPO不受高维联合动作空间对值函数估计的影响，因此在复杂任务中的表现超过了MADDPG和COMA.

4.2 与值函数分解方法的结合

如前文所述，部分早期的基于策略的方法由于需要对全局Q函数进行估计，在CTDE框架下表现不佳. 然而，随着值函数分解方法的提出，估计全局Q函数变得可行. 具体而言，值函数分解将全局Q函数分解为局部效用函数的组合以简化估计，该方式能直接应用到策略梯度方法上.

例如，DOP ^[20] 算法在COMA的基础上，使用了线性值函数分解

Q_{t o t} (s, a) = \sum_{i = 1}^{n} k_{i} (s) Q_{i} (s, a_{i}) + b (s),

(26)

并将策略梯度表示为

\nabla_{θ} J (θ) = E_{π} [\sum_{i = 1}^{n} k_{i} (s) \nabla_{θ_{i}} l o g π_{i} (a_{i} ∣ τ_{i}) Q_{i} (s, a_{i})],

(27)

此处，局部效用函数Q_i可以基于全局状态s进行计算，因为分布式执行时不需要依赖于局部效用函数的估计. 实验结果表明，DOP通过线性分解显著减少了值函数估计的方差，从而在SMAC环境中提高了性能.

然而，由于值函数分解方法本身存在的缺陷，例如线性分解表达能力不足的问题，可能导致算法无法收敛到最优值. DOP在论文中将策略评估简化为最小二乘误差（mean square error，MSE）问题，并证明了使用线性分解虽有偏差，但仍能够通过策略提升收敛到局部最优. 尽管如此，这个算法的理论性质仍然与随机策略梯度的近似全局最优性质 ^[49] 相差较远. 虽然DOP放宽了最优性要求，但从实验效果的提升表明减小全局Q函数的估计误差在算法性能方面更为重要.

类似地，FACMAC（factored multi-agent centralised policy gradients）^[21] 算法在MADDPG 的基础上，引入了QMIX的单调分解形式，即

Q_{t o t} (s, a) = f (s, {[Q_{i} (τ_{i}, a_{i})]}_{i = 1}^{n}), \frac{\partial f}{\partial Q_{i}} ⩾ 0,

(28)

并将策略梯度改写为

\begin{matrix} \nabla_{θ} J (θ) = \\ E_{s \sim D} [\nabla_{θ} μ (s) \nabla_{μ} Q_{t o t} (s, μ_{1} (τ_{1}), \dots, μ_{n} (τ_{n}))] . \end{matrix}

(29)

FACMAC不仅使用了分解后的全局 Q 函数，还通过集中式策略梯度来解决MADDPG 中的相对过度泛化（relative overgeneralization）问题 ^[50] . 具体而言，在计算智能体i的策略梯度时，其余智能体的动作不再从经验重放池中选择，而是直接通过当前策略输出，从而避免了经验回放池中的次优动作问题.

由于引入了单调值函数分解，FACMAC也继承了其固有的缺点，例如无法解决非单调矩阵博弈等问题. 值得注意的是，在基于策略的方法中，值函数分解不需要满足IGM来实现最优一致性，因为动作是由策略而不是分解后的局部效用函数决定的. 因此，在策略梯度中使用不满足IGM的非单调全局Q函数理论上仍然可行. FACMAC论文中也讨论了使用非单调函数f 进行分解的变体. 该变体在简单环境中能够克服次优性问题，但在复杂环境中效果不如单调分解. 这一现象也在RIIT（rethinking the importance of implementation tricks）算法 ^[36] 的实验中得到体现，即非单调分解理论性质更好，但在复杂任务中却不如单调分解. 这一问题会在第5节进一步讨论这一问题.

FOP算法 ^[22] 则在多智能体soft Q 学习（multi-agent soft Q-learning，MASQL）^[50] 的基础上，使用了类似 QPLEX的值函数分解方式，其全局Q函数的形式为

\begin{matrix} Q_{t o t} (s, a) = \\ \sum_{i = 1}^{n} λ_{i} (s, a) [Q_{i} (τ_{i}, a_{i}) - V_{i} (τ_{i})] + V (s), \end{matrix}

(30)

然后，每个智能体根据其局部效用函数进行策略提升

\begin{matrix} J (π_{i}) = \\ E_{τ_{i} \sim D, a_{i} \sim π_{i}} [α_{i} l o g π_{i} (a_{i} ∣ τ_{i}) - Q_{i} (τ_{i}, a_{i})] \end{matrix}

(31)

由于QPLEX的分解方法具有完全的表达能力，FOP的策略评估理论上能够收敛到正确的值. 此外，由于全局Q函数与局部效用函数的单调性（即λ_i>0），FOP的每个智能体进行策略提升后，联合策略也能得到提升. 因此，尽管FOP 引入了值函数分解，但其理论上不会因为分解而导致次优问题. 然而，FOP 也继承了QPLEX的缺点，特别是系数λ_i涉及到联合动作空间. 算法的表现会严重依赖于这些系数的准确估计.

此外，一些算法在值函数V （s）上进行了值函数分解. 例如值分解演员–评论家（value-decomposition actor-critic，VDAC）^[51]，在MAA2C的基础上将值函数V（s）进行线性和单调分解. 然而，由于V（s）本身并不涉及联合动作空间，也无需满足最优一致性，分解 V （s）更多的是网络结构上的变化. 虽然该做法可能对特征提取有所影响，但理论上并不会显著改变算法的效果.

5 进一步讨论

本节对前文介绍的算法进行总结，并进一步探讨一些观察和思考.

首先，可以发现值函数分解算法的表达能力并非越强效果就越好. 在复杂任务中，涉及联合动作空间的估计往往会带来较大的影响，尤其是在CTDE框架下; 其次，尽管在单智能体场景下基于策略的RL算法表现差异不大，但扩展为MARL时，基于Q函数的算法表现不如基于V 函数的算法. 值得一提的是，作为 off-policy算法的MADDPG理论上应具有更高的样本效率，但在多智能体环境中其表现远逊色于基于V 函数的on-policy方法; 此外，尽管有时可能会引入偏差使结果次优，将值函数分解集成到基于策略的方法上仍然能显著提升性能. 值得注意的是，所有值函数分解方法都是单调的（包括QTRAN，可由式（16）验证），即局部效用函数会随着全局Q函数的增大而增大. 而非单调的分解方法，尽管在某些情况下理论性质上更好，在实际复杂问题上往往不如单调分解方法.

这些现象目前尚未得到充分的理论解释. 接下来两小节中，本文将提出对这些问题的看法，并给出可能的改进方向.

5.1 外推误差

在这一小节中，本文将通过全局Q函数的外推误差 ^[52] 来解释这些算法遇到的问题. 回顾CTDE框架，它与直接训练n个智能体的最大不同在于需要处理高维的联合动作空间. 为了直观理解这一问题，可以以 SMAC环境为例. 若每个智能体有约10个动作，即便只有5个智能体，联合动作空间的维度也会达到10⁵，这在单智能体场景中几乎难以达成. 因此，在集中式训练下，高维的动作空间会带来显著的估计误差，从而影响算法的表现.

具体而言，联合动作空间的估计误差主要体现在 TD-target上，该误差通常被称为外推误差. 外推误差的产生源于神经网络在对于未见过或罕见输入的错误估计. 以DQN为例，其更新公式中的TD-target需要计算Q函数在（s′，a′）处的值. 需要注意的是，经验回放池中采样的是（s，a，s′），而a′则是通过策略或arg max 选出的. 因此， Q网络在（s′，a′）处可能未被充分监督，导致 TD-target的计算产生误差，从而影响 Q（s，a）的估计.

目前，外推误差主要在离线强化学习（offline RL）^[52-53] 中得到关注. 由于offline RL中数据集给定，若其中未包含动作a′，Q函数便无法准确估计该动作的值. 然而，对于在线强化学习（online RL），外推误差通常不会造成太大影响. Q函数的高估会提升对应动作的选择概率，从而收集更多相应的样本放入经验池中，进而在后续的训练中修正Q函数的高估. 然而，已有研究发现，当动作空间非常大时，外推误差仍然会产生显著影响 ^[54] . 例如SMAC环境中联合动作空间能达到10⁵，由arg max选出的动作a′所对应的Q函数值可能难以被采样到，从而显著影响Q函数的估计.

值函数分解方法的有效性正体现在它对外推误差的处理上. 通过联合动作空间的分解，值函数的估计得以简化，从而减少了TD-target中的外推误差. 然而，现有研究尚未重视这一点，一些算法在提高表达能力的同时又引入完整的联合动作空间的估计，使得在复杂环境上的性能下降. 从值函数分解的发展来看，尽管近年来不断改进分解结构，性能并未得到实质性的提升，导致目前表现最佳且最常用的算法仍是QMIX. 与策略梯度相结合的算法，虽然在将全局Q函数替换为分解后的Q函数后取得了一定的性能提升，但其根本原因尚未被充分讨论. 这也使得不少研究认为，只要采用值函数分解便能提升性能，进而推动了对V 函数进行分解的研究.

此外，online RL修正Q函数高估值的性质，实际上也依赖于值函数分解方法的单调性. 如果全局Q函数在某个动作a上被高估，则局部效用函数必须对所有动作a_i同时高估，才能增加选择a的概率，从而在后续训练中修正这一高估值. 然而，若分解结构不单调，全局Q函数的高估可能会导致局部效用函数对应的动作在后续训练中更少被选择，反而加剧外推误差的积累，这也解释了为什么非单调的QMIX在复杂任务中表现不佳.

5.2 现有方法的进一步改进

本小节将探讨一些可以基于外推误差改进现有 CTDE框架下算法的思路.

首先，尽管直接使用V 函数可以避免外推误差问题，但off-policy算法通常依赖于Q函数. 因此，在CTDE框架中，如何处理全局Q函数以及联合动作空间的外推误差是一个关键的问题. 为了更好地应对该挑战，值函数分解方法的改进可以集中在更有效地估计联合动作空间，以减少外推误差. 现有的值函数分解方法尽管有所进展，但仍有较大的性能提升空间; 另一方面，基于策略的方法通过直接优化策略来避免Q函数的外推误差，但在off-policy算法中，它们仍然需要结合 Q 函数. 为了有效减少外推误差，结合策略梯度方法与值函数分解可能是一个有前景的方向，但这也依赖于值函数分解方法的发展.

实际上，除了上述思路外，还有一些方法可以更直接地处理外推误差. 例如，许多CTDE下的算法在代码实现中都会使用多步自举（multi-step bootstrapping）技巧 ^[15]，该技巧对算法性能的影响显著，有时甚至比不同的值函数分解结构更为重要. 在MARL中，常用的多步自举方法之一是PQL（Peng’s Q（λ））^[55] . PQL与策略梯度中的广义优势函数估计 GAE（λ）（generalized advantage estimation（λ））^[56] 方法类似，其通过将TDtarget沿轨迹向后展开多步，并使用λ ∈ [0，1] 来赋予不同步数的权重，以权衡是更多依赖自举估计，还是更多依赖轨迹的回报估计. 特别地，当λ = 0 时，TDtarget就是传统的 DQN目标值，而当 λ = 1 时，TDtarget就是轨迹的累计折扣奖励

\sum_{t} γ^{t} r_{t}

. 合理地调整λ的大小，可以在Q函数估计不准确时，降低Q函数在TD-target中的权重，增加轨迹回报的权重，从而避免Q函数带来的误差，使TD-target的估计更加准确. 尽管较大的λ值可能会引入偏差导致策略次优，但实验表明，较大的λ能显著提升MARL算法在大多数任务中的表现，这也表明了处理Q函数在TD-target中外推误差的重要性.

此外，一些能够直接减少估计误差的方法，例如集成（ensemble）^[57] 等，也能显著减小外推误差. Offline RL中也有很多处理外推误差的可借鉴方法，但由于篇幅原因，这些方法在此不再详细讨论，有关内容可参考文献 ^{[52-53，58-59]} .

6 结束语

集中式训练分布式执行作为多智能体强化学习中的一种重要范式，近年来得到了广泛的关注和深入的发展. 尤其是值函数分解方法的兴起，为基于值的强化学习在复杂的多智能体任务中提供了潜力巨大的解决方案. 本文回顾了近年来CTDE框架下的主流方法，旨在为读者提供一个全面且深入的视角. 特别地，本文重点讨论了算法在估计全局Q函数时所面临的挑战和影响，提出了一些新的见解和思路. 通过分析现有算法的优缺点以及值函数分解方法在减小外推误差上的潜力，本文为后续算法的改进和发展提供了一些有价值的思考. 希望这些讨论能够为今后多智能体强化学习领域的研究者们提供新的思路，并推动该领域的进一步发展.

图1合作多智能体强化学习顶会论文近年发表情况

Fig.1Top conference publication status of collaborative MARL papers in recent years

下载: 全尺寸图片

图2过去几年论文中算法出现次数的对比

Fig.2Comparison of the number of algorithm occurrences in the past few years

下载: 全尺寸图片

表1代表性算法

Table1Representative algorithms

下载: 全尺寸图片

图1合作多智能体强化学习顶会论文近年发表情况

Fig.1Top conference publication status of collaborative MARL papers in recent years

图2过去几年论文中算法出现次数的对比

Fig.2Comparison of the number of algorithm occurrences in the past few years

表1代表性算法

Table1Representative algorithms

图1合作多智能体强化学习顶会论文近年发表情况

Fig.1Top conference publication status of collaborative MARL papers in recent years

图2过去几年论文中算法出现次数的对比

Fig.2Comparison of the number of algorithm occurrences in the past few years

表1代表性算法

Table1Representative algorithms

KIM J H, VADAKEPAT P. Multi-agent systems: A survey from the robot-soccer perspective. International Journal of Intelligent Automation and Soft Computing,2000,6(1):3-17.

ZHANG K, YANG Z, BAS¸AR T. Multi-agent reinforcement learning: A selective overview of theories and algorithms. Handbook of Reinforcement Learning and Control. Cham: Springer,2021:321-384.

OROOJLOOY A, HAJINEZHAD D. A review of cooperative multi-agent deep reinforcement learning. Applied Intelligence,2023,53(11):13677-13722.

ZHOU M, LUO J, VILLELLA J,et al. Smarts: An open-source scalable multi-agent rl training school for autonomous driving. Conference on Robot Learning. New York: PMLR,2021:264-285.

SINGH A J, KUMAR A, LAU H C. Hierarchical multiagent reinforcement learning for maritime traffic management. Proceedings of the 19th International Conference on Autonomous Agents and MultiAgent Systems. Richland: IFAAMAS,2020:1278-1286.

HUTTENRAUCH M,¨ SOˇ SIˇ C A, NEUMANN G. Guided deep rein-´ forcement learning for swarm systems. ArXiv Preprint,2017, ArXiv:1709.06011.

ZHANG T, LI Y, LI S,et al. Decentralized circle formation control for fish-like robots in the real-world via reinforcement learning. IEEE International Conference on Robotics and Automation. Piscataway: IEEE,2021:8814-8820.

FRANS A O, MATTHIJS T J S, NIKOS V. Optimal and approximate Q-value functions for decentralized pomdps. Journal of Artificial Intelligence Research,2008,32:289-353.

LANDON K, BIKRAMJIT B. Multi-agent reinforcement learning as a rehearsal for decentralized planning. Neurocomputing,2016,190:82-94.

SUNEHAG P, LEVER G, GRUSLYS A,et al. Value-decomposition networks for cooperative multi-agent learning. ArXiv Preprint,2017, ArXiv:1706.05296.

RASHID T, SAMVELYAN M, DE WITT C S,et al. Monotonic value function factorisation for deep multi-agent reinforcement learning. Journal of Machine Learning Research,2020,21(178):1-51.

PAPOUDAKIS G, CHRISTIANOS F, SCHAFER L,et al. Bench-¨ marking multi-agent deep reinforcement learning algorithms in cooperative tasks. ArXiv Preprint,2020, ArXiv:2006.07869.

YU C, VELU A, VINITSKY E,et al. The surprising effectiveness of PPO in cooperative multi-agent games. Advances in Neural Information Processing Systems. Red Hook: Curran Associates,2022:24611-24624.

GORSANE R, MAHIOUB O, DE KOCK R,et al. Towards a standardised performance evaluation protocol for cooperative marl. Advances in Neural Information Processing Systems. Red Hook: Curran Associates,2022:5510-5521.

RICHARD S S, ANDREW G B. Reinforcement Learning: An Introduction. Cambridge: MIT Press,1998.

SON K, KIM D, KANG W J,et al. Qtran: Learning to factorize with transformation for cooperative multi-agent reinforcement learning. International Conference on Machine Learning. New York: PMLR,2019:5887-5896.

WANG J, REN Z, LIU T,et al. QPLEX: Duplex dueling multi-agent Q-learning. ArXiv Preprint,2020, ArXiv:2008.01062.

LOWE R, WU Y I, TAMAR A,et al. Multi-agent actor-critic for mixed cooperative-competitive environments. Advances in Neural Information Processing Systems. Red Hook: Curran Associates,2017:6382-6393.

FOERSTER J, FARQUHAR G, AFOURAS T,et al. Counterfactual multi-agent policy gradients. Proceedings of the AAAI Conference on Artificial Intelligence. New Orleans: AAAI Press,2018:2974-2982.

WANG Y, HAN B, WANG T,et al. DOP: Off-policy multi-agent decomposed policy gradients. ArXiv Preprint,2020, ArXiv:2007.12322.

PENG B, RASHID T, SCHROEDER D W C,et al. FACMAC: Factored multi-agent centralised policy gradients. Advances in Neural Information Processing Systems. Red Hook: Curran Associates,2021:12208-12221.

ZHANG T, LI Y, WANG C,et al. FOP: Factorizing optimal joint policy of maximum-entropy multi-agent reinforcement learning. International Conference on Machine Learning. New York: PMLR,2021:12491-12500.

FRANS A O, CHRISTOPHER A. A Concise Introduction to Decentralized POMDPs. Cham: Springer International Publishing,2016.

WATKINS C J C H, DAYAN P. Q-learning. Machine Learning,1992,8:279-292.

MNIHV, KAVUKCUOGLU K, SILVER D,et al. Humanlevel control through deep reinforcement learning. Nature,2015,518(7540):529-533.

TAN M. Multi-agent reinforcement learning: Independent vs.cooperative agents. Proceedings of the tenth International Conference on Machine Learning. San Francisco: Morgan Kaufmann,1993:330-337.

HAUSKNECHT M, STONE P. Deep recurrent Q-learning for partially observable MDPs. AAAI Fall Symposium Series. Arlington: AAAI Press,2015:141-145.

TAMPUU A, MATIISEN T, KODELJA D,et al. Multiagent cooperation and competition with deep reinforcement learning. PloS One,2017,12(4):e0172395.

SILVER D, LEVER G, HEESS N,et al. Deterministic policy gradient algorithms. International Conference on Machine Learning. New York: PMLR,2014:387-395.

SCHULMANl J, WOLSKI F, DHARIWAL P,et al. Proximal policy optimization algorithms. ArXiv Preprint,2017, ArXiv:1707.06347.

LILLICRAP T P, HUNT J J, PRITZEL A,et al. Continuous control with deep reinforcement learning. ArXiv Preprint,2015, ArXiv:1509.02971.

DE W C S, GUPTA T, MAKOVIICHUK D,et al. Is independent learning all you need in the starcraft multi-agent challenge?ArXiv Preprint,2020, ArXiv:2011.09533.

CHANG Y H, HO T, KAELBLING L. All learning is local: Multiagent learning in global reward games. Advances in Neural Information Processing Systems. Cambridge: MIT Press,2003:807-814.

VASWANI A. Attention is all you need. Advances in Neural Information Processing Systems. Red Hook: Curran Associates,2017:6000-6010.

YANG Y, HAO J, LIAO B,et al. Qatten: A general framework for cooperative multiagent reinforcement learning. ArXiv Preprint,2020, ArXiv:2002.03939.

HU J, JIANG S, HARDING S A,et al. Rethinking the implementation tricks and monotonicity constraint in cooperative multi-agent reinforcement learning. ArXiv Preprint,2021, ArXiv:2102.03479.

DOU Z, KUBA J G, YANG Y. Understanding value decomposition algorithms in deep cooperative multi-agent reinforcement learning. ArXiv Preprint,2022, ArXiv:2202.04868.

WANG J, REN Z, HAN B,et al. Towards understanding linear value decomposition in cooperative multi-agent q-learning. Advances in Neural Information Processing Systems. Red Hook: Curran Associates,2021:29142-29155.

ELLIS B, COOK J, MOALLA S,et al. SMACv2: An improved benchmark for cooperative multi-agent reinforcement learning. Advances in Neural Information Processing Systems. Red Hook: Curran Associates,2023:37567-37593.

HA D, DAI A, LE Q V. Hypernetworks. ArXiv Preprint,2016, ArXiv:1609.09106.

MAHAJAN A, RASHID T, SAMVELYAN M,et al. MAVEN: Multiagent variational exploration. Advances in Neural Information Processing Systems. Red Hook: Curran Associates,2019.

RASHID T, FARQUHAR G, PENG B,et al. Weighted QMIX: Expanding monotonic value function factorisation for deep multi-agent reinforcement learning. Advances in Neural Information Processing Systems. Red Hook: Curran Associates,2020,33:10199-10210.

SON K, AHN S, REYES R D,et al. QTRAN++: Improved value transformation for cooperative multi-agent reinforcement learning. ArXiv Preprint,2020, ArXiv:2006.12010.

LI Y, XIE G, LU Z. Difference advantage estimation for multi-agent policy gradients. International Conference on Machine Learning. New York: PMLR,2022:13066-13085.

ZHOU M, LIU Z, SUI P,et al. Learning implicit credit assignment for cooperative multi-agent reinforcement learning. Advances in Neural Information Processing Systems. Red Hook: Curran Associates,2020:11853-11864.

YANG M, ZHAO J, HU X,et al. LDSA: Learning dynamic subtask assignment in cooperative multi-agent reinforcement learning. Advances in Neural Information Processing Systems. Red Hook: Curran Associates,2022,35:1698-1710.

LI J, KUANG K, WANG B,et al. Shapley counterfactual credits for multi-agent reinforcement learning. Proceedings of the 27th ACM SIGKDD Conference on Knowledge Discovery & Data Mining. New York: ACM,2021:934-942.

SAMVELYAN M, RASHID T, DE WITT C S,et al. The starcraft multi-agent challenge. ArXiv Preprint,2019, ArXiv:1902.04043.

AGARWAL A, KAKADE S M, LEE J D,et al. On the theory of policy gradient methods: Optimality,approximation,and distribution shift. Journal of Machine Learning Research,2021,22(98):1-76.

WEI E, WICKE D, FREELAN D,et al. Multiagent soft Q-learning. ArXiv Preprint,2018, ArXiv:1804.09817.

SU J, ADAMS S, BELING P. Value-decomposition multi-agent actor-critics. Proceedings of the AAAI Conference on Artificial Intelligence. Menlo Park: AAAI Press,2021:11352-11360.

FUJIMOTO S, MEGER D, PRECUP D. Off-policy deep reinforcement learning without exploration. International Conference on Machine Learning. New York: PMLR,2019:2052-2062.

LEVINE S, KUMAR A, TUCKER G,et al. Offline reinforcement learning: Tutorial,review,and perspectives on open problems. ArXiv Preprint,2020, ArXiv:2005.01643.

FUJIMOTO S, CHANG W D, SMITH E,et al. For sale:state-action representation learning for deep reinforcement learning. Advances in Neural Information Processing Systems. Red Hook: Curran Associates,2024:36.

KOZUNO T, TANG Y, ROWLAND M,et al. Revisiting peng’s Q(λ)for modern reinforcement learning. International Conference on Machine Learning. New York: PMLR,2021:5794-5804.

SCHULMAN J, MORITZ P, LEVINE S,et al. High-dimensional continuous control using generalized advantage estimation. ArXiv Preprint,2015, ArXiv:1506.02438.

ANSCHEL O, BARAM N, SHIMKIN N. Averaged-DQN: Variance reduction and stabilization for deep reinforcement learning. International Conference on Machine Learning. New York: PMLR,2017:176-185.

AN G, MOON S, KIM J H,et al. Uncertainty-based offline reinforcement learning with diversified Q-ensemble. Advances in Neural Information Processing Systems. Red Hook: Curran Associates,2021:7436-7447.

BAI C, WANG L, YANG Z,et al. Pessimistic bootstrapping for uncertainty-driven offline reinforcement learning. ArXiv Preprint,2022, ArXiv:2202.11566.