欢迎访问《控制理论与应用》期刊网站！

一类三维装箱问题的多智能体分层强化学习求解算法研究

doi: 10.7641/CTA.2025.50058

初阳^1,2 ，燕雪峰^1,3 ，张玄烨⁴ ，徐云雯⁴ ，李德伟⁴

1. 南京航空航天大学计算机科学与技术学院, 江苏南京 211106

2. 江苏自动化研究所, 江苏连云港 222061

3. 中国南京软件新技术与产业化协同创新中心, 江苏南京 210023

4. 上海交通大学自动化系, 上海 200240

详细信息

作者简介

初阳副研究员,目前研究方向为智能系统算法,E-mail: chuyang716@163.com;

燕雪峰教授,目前研究方向为人工智能相关算法,E-mail: yxf@nuaa.edu.cn;

张玄烨硕士研究生,目前研究方向为智能强化学习方法,E-mail: xuanye-z22@sjtu.edu.cn;

徐云雯副研究员,目前研究方向为智能系统决策与优化,E-mail: willing419@sjtu.edu.cn;

李德伟教授,目前研究方向为复杂系统建模与优化控制,E-mail: dwli@sjtu.edu.cn.

通信作者

李德伟，E-mail: dwli@sjtu.edu.cn;Tel.:+8621-34204550.

Research on multi-agent hierarchical reinforcement learning algorithm for solving one type of 3D bin packing problem

CHU Yang^1,2 ， YAN Xue-feng^1,3 ， ZHANG Xuan-ye⁴ ， XU Yun-wen⁴ ， LI De-wei⁴

1. School of Computer Science and Technology, Nanjing University of Aeronautics and Astronautics, Nanjing Jiangsu 211106 , China

2. Jiangsu Automation Research Institute, Lianyungang Jiangsu 222061 , China

3. Collaborative Innovation Center of Novel Software Technology and Industrialization. Nanjing Jiangsu 210023 , China

4. Department of Automation, Shanghai Jiao Tong University, Shanghai 200240 , China

摘要

针对半在线场景下的多箱体三维装箱问题(3D-BPP), 为了提高装箱决策效率和装箱空间利用率, 本文提出一种多智能体分层强化学习算法. 该算法采用多智能体马尔可夫决策过程(MAMDP)对问题进行建模, 通过3个完全合作的智能体分别负责货物选择、箱子选择和摆放位置规划, 并引入值分布学习方法以增强算法的稳定性和收敛性. 实验结果表明, 该算法在不同环境配置下均表现出良好的性能, 空间利用率和装入货物数量显著提升, 且在多箱体和多货物选择场景下展现出较强的泛化能力. 与传统的启发式算法相比, 该算法在动态决策和适应性方面具有明显优势, 尤其在处理未知分布的货物尺寸时表现出较强的鲁棒性. 该算法首次将多智能体分层强化学习框架应用于3D-BPP, 实现装箱决策的端到端优化, 为复杂装箱场景提供了一种新颖的解决方案.

关键词

三维装箱问题 / 深度强化学习 / 多智能体强化学习 / 组合优化

Abstract

With consideration of the complexity of the three-dimensional bin packing problem (3D-BPP) in the multibin semi-online scenarios, a multi-agent hierarchical reinforcement learning algorithm is proposed to improve packing efficiency and space utilization. The proposed algorithm models the problem by using a multi-agent Markov decision process (MAMDP), including three fully cooperative agents responsible for item selection, bin selection, and placement planning, respectively. A distributional learning method is introduced to enhance the stability and convergence of the algorithm. Experimental results demonstrate that the algorithm exhibits superior packing performance across various environmental configurations, significantly improving space utilization and the number of packed items. It also shows strong generalization capabilities in multi-bin and multi-item selection scenarios. Compared to traditional heuristic algorithms, the proposed method has clear advantages in dynamic decision-making and adaptive optimization, particularly demonstrating robustness when handling items with unknown size distributions. The innovation lies in the first application of a multi-agent hierarchical reinforcement learning framework to the 3D-BPP, achieving end-to-end optimization of packing decisions and providing a novel solution for complex packing scenarios.

Keywords

three-dimensional packing problem / deep reinforcement learning / multi-agent reinforcement learning / combinatorial optimization

1 引言 2 多箱体半在线装箱问题 3 装箱问题的深度强化学习建模 4 多智能体强化学习装箱算法设计 4.1 策略神经网络结构设计 4.2 分层决策的多智能体合作学习装箱算法 5 实验验证 5.1 实验设置 5.2 不同场景设置下的装箱算法性能指标 5.3 对比实验与泛化能力实验 6 结论

1 引言

随着电商与制造业的快速发展，如何高效地利用有限的资源成为了现代化工业和商业领域中的关键问题. 三维装箱问题（3D bin packing problem，3D-BPP）作为一种典型的组合优化问题，其研究成果直接影响到自动化仓储系统，智能物流配送和运输优化等核心技术环节. 在一般化的装箱场景下，货物按照某个预设顺序依次到达，装箱系统可以预览序列中接下来的若干货物，从中选择货物并与多个箱子进行匹配，执行器（通常是机械臂或吊具等）将选中货物放入箱子中的合适位置. 这种场景也被称为多箱体的半在线装箱问题，其中涉及货物装载顺序规划、箱子选择、位置规划多个决策环节. 装箱任务的目标是在最大化空间利用率的同时，尽量减少所需箱子的数. 由于3D-BPP 属于NP难问题，寻找全局最优解通常需要付出极高的计算代价，因此如何高效解决3D-BPP是一个既具有理论价值又具有实践意义的问题.

对于三维装箱问题中的不同决策环节，传统的解决方案是启发式算法，研究者们主要关注的是位置规划阶段. 针对这一问题，Tresca等人 ^[1] 用物体依次形成平面或块来模仿人工装箱，Liu等人 ^[2] 和Tseremoglou等人 ^[3] 分别使用了角点与极点的候选摆放位置，结合剪枝搜索策略降低解空间的复杂度. 文献 ^[4] 采用根据实际业务场景设计的多指标加权和作为指标，针对货物装载顺序规划需要在装箱前或装箱时对货物进行排序解决装载顺序的问题. 此外，研究者也设计了基于适应值的箱子选择方法，根据各箱子当前空间占有情况以及物体体积计算出物体相对于箱子的适应值从而排序选取 ^[5] . 对于与业务相关的相关约束，沈倪等人 ^[6] 针对考虑温层和冷媒装载约束的冷链商品多箱型装箱问题提出了一种融合启发式算法，李潇 ^[7] 在其提出的3D-BPP算法中重点关注了与机器人实现相关的装箱约束. 而在包含人类参与的装箱任务中，徐翔斌等人 ^[8] 将最大空间法与有偏随机密钥遗传算法结合，在不增加装箱成本的前提下提高了装卸工的作业姿势舒适度. 启发式算法的实现难度不高，在预设规则引导下的装箱决策行为也具有一定的可解释性，但随着问题规模的扩大，在给定求解时间的限制下算法性能退化严重. 同时，启发式算法的设计也高度依赖人类专家的领域知识，因此，针对特定场景设计新的启发式装箱求解算法是一项困难的任务.

随着深度学习技术的快速发展，研究者们将装箱问题的求解建模为一个马尔可夫决策过程，利用深度强化学习解决了单箱子的在线装箱中的位置规划问题. 例如，采用鸟瞰图的方式表示箱子内部的状态，利用卷积神经网络提取特征 ^[9]; 赵航等人 ^[10] 提出一种树状结构的状态表示方法，利用强化学习引导启发式算法的搜索过程，极大缩小了决策空间，并取得了较好的性能. 利用深度强化学习求解装箱问题时，研究者们重点关注如何学习到更好的物品摆放策略，然而在多箱体选择和预览货物选择等决策环节仍以预设规则为主，这导致了算法对专家经验仍有一定程度的依赖，且算法性能指标仍具有提升空间. 因此，针对三维装箱问题中的箱体选择和预览货物选择等其他决策环节，设计统一的数据驱动学习算法具有重要的理论与实践意义.

针对一种多箱体的半在线装箱问题，为了摆脱其问题求解对人类经验的依赖，提高装箱算法的性能，本文提出一种多智能体分层决策的深度强化学习算法. 该方法利用问题的多阶段特点，将原问题建模成一个多智能体马尔可夫决策过程，进而利用多个完全合作的智能体以分层决策方式完成一次装箱操作中的箱子选择、货物选择及摆放位置规划等任务. 在多智能体的训练阶段引入了值分布的学习方法，增强了深度强化学习算法的稳定性和收敛性能. 论文在多种环境配置下进行实验验证，同多种启发式算法相比，论文所提出算法都取得了更优秀的装箱性能指标，并且学习到的分层决策装箱策略也具备一定的泛化能力.

2 多箱体半在线装箱问题

在多箱体的半在线装箱场景中，待装箱的货物依次到达装箱操作位置; 装箱执行器在装箱操作位置的范围内，通过相机等感知设备感知货物的尺寸，并从待装箱的多个货物中选择一个进行抓取; 装箱执行器在多个装货用箱子中选择一个目标箱子，将抓取的货物放在箱子的合适位置. 图1展示了这一流程，在这一场景中，通常假设待装货物为长方体，感知设备可以感知待装货物的尺寸以及各个箱子的目前状态（剩余空间大小）. 装箱算法的目标是最大化所有箱子的空间利用率，即在单位空间内容纳更多的货物，从而提升整体装箱效率和资源利用率.

图1多箱体Semi-online3D BPP场景示意图

Fig.1Multi-bin semi-online packing scenario

为了对上述多箱体半在线装箱问题进行数学描述，将箱子的集合记作B = {B₁，B₂，· · · }，|B|=b为可供选择的箱子个数. 对于j = 1，2，· · ·，b，箱子B_j的尺寸记作三元组（S_jx， S_jy，S_jz），其中x，y，z分别为三维空间中的坐标轴. 对于到达装箱位置的货物，p为装箱算法能观测并选择的货物的数量，J 表示到达的货物序列集. 对于每一个货物i ∈ J，其沿坐标轴方向的尺寸可表示为三元组（s_ix，s_iy，s_iz），分别为其沿x，y，z方向的长度. 货物i在箱子中的位置表示为三元组（p_ix，p_iy，p_iz），即其前左下（front-left-bottom，FLB）角点坐标，坐标系原点为箱子的FLB角点. 假设

J_{B_{j}} \subset J

表示箱子B_j中已装入货物的集合，

J^{'} = ⋃_{j = 1}^{b} J_{B_{j}}

为所有已装箱货物的集合，t_i表示货物i被放入箱子的时间步，index_i表示货物i在

J

中的位置索引（从0开始），0–1 变量M_ij用于指示货物i是否被放入了箱子B_j. C_i是货物i与其支撑物体的接触边界形成的凸多边形在 xoy平面内的2D投影. 根据上述定义，多箱体半在线装箱问题可以表述为如下的组合优化问题:

\begin{matrix} M a x i m i z e : \frac{1}{b} \sum_{j = 1}^{b} \frac{\sum_{i \in J_{B_{j}}} s_{i x} s_{i y} s_{i z}}{S_{j x} S_{j y} S_{j z}}, \\ s . t . p_{i d} + s_{i d} ⩽ p_{i^{'} d}, \forall i, i^{'} \in J_{B_{j}}, \end{matrix}

(1)

i \neq i^{'}, d \in {x, y, z}

(2)

\begin{matrix} 0 ⩽ M_{i j} \cdot p_{i d} ⩽ S_{j d} - s_{i d} \\ \forall i \in J^{'}, j = 1,2, \dots, b, \end{matrix}

(3)

{index}_{i} - t_{i} < p, \forall i \in J^{'},

(4)

\sum_{j = 1}^{b} M_{i j} = 1, \forall i \in J^{'},

(5)

(p_{i x} + \frac{1}{2} s_{i x}, p_{i y} + \frac{1}{2} s_{i y}) \in C_{i}, \forall i \in J^{'},

(6)

在优化问题（1）–（6）中，目标函数式（1）定义了所有箱子的平均空间利用率，即装箱算法的优化目标为最大化所有箱子的平均空间利用率; 式（2）保证了同一箱子内的货物不得存在空间重叠; 式（3）则限制货物的摆放不得超出箱子的边界范围; 式（4）描述了装箱算法在决策时仅能预览接下来k个货物并从中选择; 式（5）是0–1 变量的约束条件，确保每个货物只能被放置到一个箱子中; 式（6）为装箱稳定性约束. 上述优化问题的目标函数也可以通过调整不同箱子空间利用率的权值，来适应对于箱子的不同要求.

3 装箱问题的深度强化学习建模

强化学习中采用马尔可夫决策过程（Markov decision process，MDP）建模具有决策行为的动态系统，定义了智能体（agent）与环境之间的交互过程，智能体能够根据观测到的环境状态信息并采取对应动作，并在与环境进行交互后获得来自环境的反馈信号，并从反馈信号中进行学习. 一个MDP可以表示为一个五元组（S，A，P，r，γ），其中: 状态空间S表示系统或环境可能的所有状态集合，动作空间A表示智能体可执行的所有动作集合， P（s ′ |s，a）表示智能体在状态s时执行动作a后转移到状态s ′的概率分布，奖励函数r表示智能体执行动作后从环境中获取的反馈信号，折扣因子γ用于度量未来奖励在当前时刻的相对重要性.

强化学习智能体的目标是找到一个最优策略π^∗使得从任意初始状态开始的累积期望奖励最大化，如式（7）所示，其中策略π（a|s）表示状态s下执行各动作的概率分布.

π^{*} = a r g \underset{π}{m a x} E_{a \sim π (a ∣ S)} \sum_{t = 0}^{\infty} γ^{t} r_{t + 1} .

(7)

对于本文中研究的多箱体半在线装箱问题，单次装入货物的行为包括3个决策步骤: 货物选择，箱子选择，摆放位置规划，可以采用3个智能体分别完成这3 类决策任务. 此时的MDP可以扩展为多智能体马尔可夫决策过程（multi-agent Markov decision process，MAMDP），即多个智能体共享一个全局的状态空间，每个智能体都可以采取动作，系统的状态转移由所有智能体的联合动作决定. 在装箱问题的求解过程中，这 3个智能体是完全合作的，共享式（1）所示的优化目标. 因此，可以采用MAMDP对涉及多个箱子和货物排序的3D-BPP求解过程进行建模，并采用多智能体强化学习算法以学习最优的装箱策略.

状态: 对于货物选择智能体π_i和箱子选择智能体 π_b，其时间步t的状态S_t包括以下两个部分: 已装入货物位置信息B_t表示当前已经装入箱子中的货物及其位置的状态，这些信息通常包括货物的尺寸、位置、朝向等参数，帮助智能体评估当前装箱状态，估计待装物体对未来其他物造成的潜在影响; 可预览货物尺寸信息I_t表示当前时间步可以预览到的p个货物的尺寸，这些信息有助于智能体判断哪些货物适合放入当前箱子. 在完成货物选择和箱子选择后，位置规划智能体π_p的状态S_t除以上两部分还额外包括L_t，即当前货物在选择的目标箱子中候选的放置位置，可以由最大空间策略等启发式规则计算. B_t和L_t中每个元素可以表示为形如（s_x，s_y，s_z，p_x，p_y，p_z，d）的向量，冗余位d 中记录了货物所在箱子的索引，从而建立起货物和箱子的关联. 冗余位也包含了有关货物属性的相关信息，用于处理例如放置稳定性等现实约束. I_t中的每个元素则为可观测物体的尺寸向量（s_x，s_y，s_z）. 通过这样的状态表示，货物选择，箱子选择和位置规划的决策能够互相衔接，有效地提高系统的整体性能.

动作: MAMDP的联合动作空间由这些低维离散决策空间复合而成，货物选择策略π_i的动作信号对应被选中货物在可预览货物序列中的索引，其动作空间的维度为p，即可预览的货物数量. 箱子选择策略π_b的动作信号为被选中箱子在当前箱子列表中的索引，动作空间的维度为b，即当前可用的箱子数量. 而位置规划策略πp 的动作信号为最终摆放位置在候选位置集合中的索引，其动作空间的维度为|L_t|，即当前时间步中通过一步启发式搜索所得的候选摆放位置数量. 上述3个智能体的动作空间均为离散且维度有限的，这种设计有效降低了MAMDP求解最优策略的复杂性，从而提升了多智能体强化学习算法的训练效率与收敛性.

奖励: 货物选择，箱子选择和摆放位置规划这3个决策环节合作完成装箱任务，符合完全合作多智能体强化学习范式. 因此，它们共享相同的奖励函数，以促使3个智能体在同一目标下共同优化装箱策略. 奖励函数r被设计为每成功放入一个货物时，箱子空间利用率的增量. 具体而言，对于时间步t放入的货物i_t和放入的箱子b_t，其即时奖励信号可由式（8）计算得到，其中: c_r为一个缩放常数，（

s_{i_{t} x} ， s_{i_{t y}} ， s_{i_{t z}} .

）为货物i_t的尺寸，（

s_{b_{t} x} ， s_{b_{t} y} ， s_{b_{t} z}

）为箱子b_t的尺寸.

r_{t} = c_{r} \cdot \frac{s_{i_{t x}} s_{i_{t y}} s_{i_{t z}}}{s_{b_{t x}} s_{b_{t y}} s_{b_{t z}}}

(8)

终止信号: 在以上的奖励函数中仅包含了成功放

入货物的情形，而当智能体的装箱决策违反了式（2）–（6）中的约束条件时，引入了一个计数器用于记录违反几何尺寸约束的次数. 当违反次数较少时，当前的装箱步骤不会对环境状态做出任何改变，即不进行物品的摆放，获得的即时奖励为0; 若计数器的值超过某个预设的阈值，则强制终止当前装箱流程，返回终止信号，并将所有箱子替换为空箱，随后重置环境，计数器归零. 终止信号和奖励信号的计算方法如图2所示.

4 多智能体强化学习装箱算法设计

4.1 策略神经网络结构设计

本文中涉及的箱子选择，货物选择，位置规划3个智能体分别利用3个神经网络π_b，π_i，π_p进行决策，且具有相似的结构，仅在输入信息与输入输出维度上有所区别，如图3所示. 货物选择智能体π_i，箱子选择智能体π_b分别接受所有箱子中已装箱货物的信息B以及预览货物的尺寸信息I作为输入，并分别采用

ψ_{θ_{b}}

与

ψ_{θ_{i}}

两个多层感知机（multi-layer perceptron，MLP）提取低阶特征f_l . π_p的输入则为被选中箱子中已装箱货物的信息B′以及被选中货物尺寸i，此外还包括该货物在该箱子中的候选摆放位置L，并利用MLP

ψ_{θ_{p}}

提取特征.

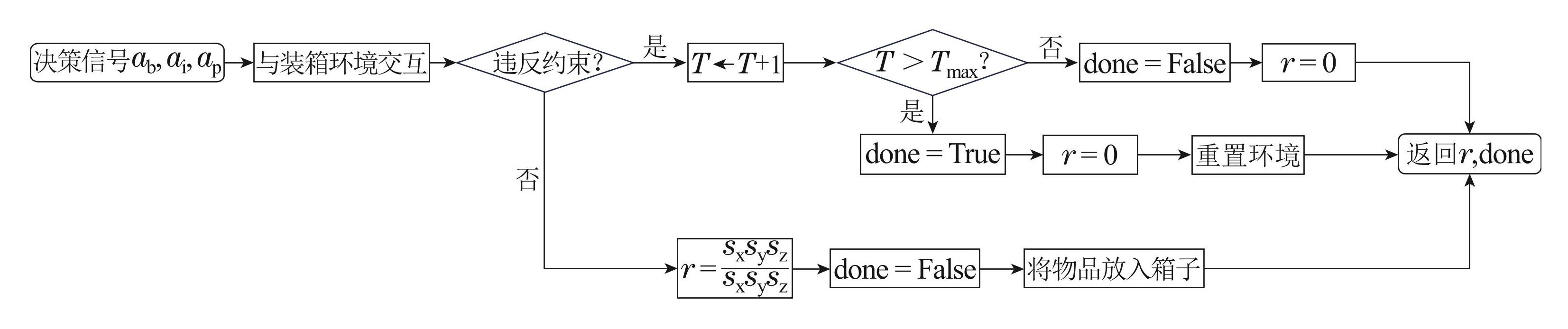
图2奖励与终止信号计算流程图

Fig.2The flowchart of calculating reward and terminal signal

图3神经网络模型结构示意图

Fig.3Neural network structure

随后采用Transformer ^[11] 结构中的自注意力机制进行高层次特征的提取. 在单个自注意力块中，先使用3个线性层Q， K，V 对输入进行投影，再计算缩放点积自注意力得分，最后经过归一化和前馈网络，其中还包括稳定训练所用的残差连接. 经过若干次自注意力块后得到高级特征f_h.

动作头部分包括两个噪声网络分别计算值函数与优势函数，记作V（· | σ_V）和A （· | σ_A），其中σ_V，σ_A分别为噪声标准差. 神经网络最终输出q∈

R^{N_{axtion} \times N_{atomis}}

，其中: N_action 为各智能体的动作空间维度，N_atoms为值分布学习的支持向量维度. q（s，a）（i）表示智能体在状态s下采取动作a的回报落在区间[z^（ⁱ^），z^（ⁱ^+1）]上的概率，可由式（9）计算，其中

{\bar{A}}^{(j)} (f_{h}) = \frac{1}{N_{action}} \sum_{a^{'} \in A} A^{(j)} (f_{h}, a^{'} ∣ σ_{A}) .

q^{(i)} (s, a) = \frac{\exp (V^{(i)} (f_{h} ∣ σ_{V}) + A^{(i)} (f_{h}, a ∣ σ_{A}))}{\sum_{j = 1}^{N_{action}} e x p (V^{(j)} (f_{h} ∣ σ_{V}) + A^{(j)} (f_{h}, a ∣ σ_{A})) - {\bar{A}}^{(j)} (f_{h})} .

(9)

4.2 分层决策的多智能体合作学习装箱算法

在本文研究的多箱体半在线装箱场景下，装入单个货物的步骤可以被描述为多智能体的两阶段分层决策流程，如图4所示. 第1层决策中货物选择智能体和箱子选择智能体确定当前步骤被装入的货物与装入的目标箱子，而第 2层决策中先采用 EMS（empty maximal spaces）启发式算法 ^[12] 计算货物在对应箱子中的候选摆放位置列表，再利用位置规划智能体在候选列表中进行选择，如图5所示.

图4单步装箱中的分层合作决策流程

Fig.4The hierarchical collaborative decision process in one packing step

智能体在状态 s_t下根据神经网络输出值选择最优动作a^∗，如式（10）所示，其中z^（ⁱ^） = V_min+（i−1）×

\frac{V_{m a x} - V_{m i n}}{N_{atoms}}

为价值分布在区间[V_min，V_max]上的离散化取值点

a^{*} = \underset{a \in A}{a r g m a x} \sum_{i = 1}^{N_{atoms}} z^{(i)} \cdot q_{θ}^{(i)} (s_{t}, a) .

(10)

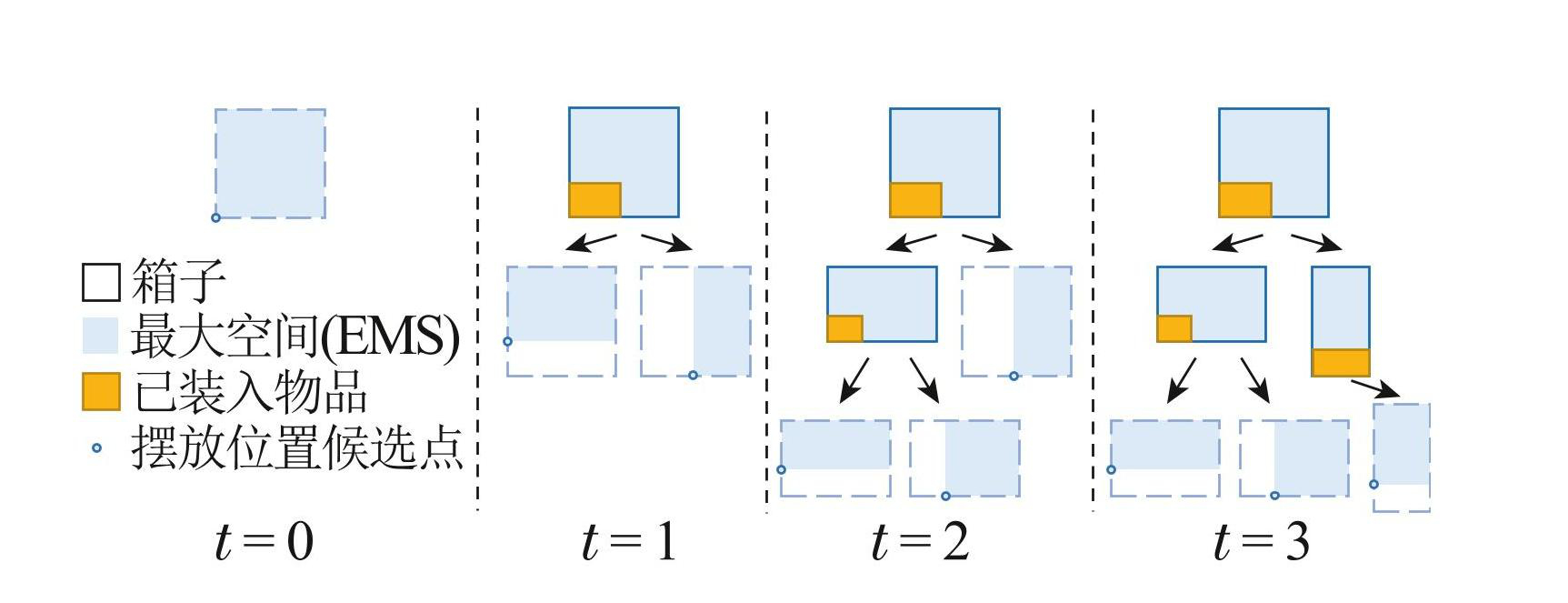
图5利用EMS启发式方法生成候选摆放位置

Fig.5Generating placement candidates with EMS heuristic

每装入一个货物后，3个智能体以四元组（s_t，a_t，s_t₊₁，r_t）的形式将与环境的交互记录存入各自的经验回放缓存，并以相同的频率从缓存中采样一定批次经验数据进行训练. 智能体均采用Rainbow强化学习算法 ^[13] 进行训练，按图6所示的流程计算批次数据的损失. 首先由当前网络预测t时刻的回报分布 d_t =（z，q_θ（s_t，a_t）），即P（d_t = z^（ⁱ^））=

q_{θ}^{(i)} (s_{t} ， a_{t})

，再根据式（10）选取t + n 时刻的最优动作并计算实际回报分布

d_{t}^{'} = (g_{t}^{(n)} + γ^{n} Z ， q_{θ^{'}} (s_{t + n} ， a_{t + n}^{*})) ，

其中

g_{t}^{(n)}

为t时间步的n步回报. 利用L2投影将

d_{t}^{'}

的概率质量重新分配到z的支持点上得到Φ_z（

d_{t}^{'}

）. 因此，批次内该数据产生的损失贡献l可由

d_{t}^{'}

与Φ_z（

d_{t}^{'}

）的KL散度衡量，可由式（11）计算得到.

l = D_{K L} (Φ_{z} (d_{t}^{'}) ‖ d_{t}^{'}) = \sum Φ_{z} (d_{t}^{'}) l o g \frac{Φ_{z} (d_{t}^{'})}{d_{t}^{'}}

(11)

图6Rainbow算法流程示意图

Fig.6Flowchart of the Rainbow algorithm

总体损失L是l对经验采样权重w的加权平均，进而利用Adam优化器完成神经网络参数的梯度下降更新. 最后修改当前采样批次数据中的经验采样权重，与该条数据产生的损失值l呈正相关. 更大的损失值表示该条数据上仍有较高的学习潜力，下次采样时应该具有更大的权重. 训练过程中噪声网络标准差周期性地衰减然后重置，以平衡智能体的探索与利用.

5 实验验证

5.1 实验设置

在实验场景中，假设所有箱子是底面积100，高为 10的上方开口长方体，可选长宽比包括1:1，4:3，16:9. 在每次新的装箱流程开始时，从均匀分布U（1，5）中随机采样150个物体的尺寸作为待装货物的序列. 在不违反约束的前提下，货物可放置于箱子中的任意位置. 考虑到物理实现中的限制，为了便于机械臂的抓取与放置路径规划，物体的摆放方向自由度为2，即物体只能在与箱子边缘正交的两个水平方向上进行摆放. 评估阶段，观察装箱智能体在完成100次装箱流程后的表现，主要通过以下几个指标进行衡量: 空间利用率的均值，成功装入物体的数量的均值，以及空间利用率的方差.

强化学习环境和本文提出的算法均由Python实现，所有实验均在配备RTX 3090 GPU的Linux服务器上进行. 训练直至平均奖励值与损失函数值不再明显变化为止，装箱智能体与环境交互至多600万次. 实验过程中的相关超参数由网格搜索确定，如表1所示.

表1实验超参数

Table1Hyperparameters in our experiments

5.2 不同场景设置下的装箱算法性能指标

对于本文研究的多箱子半在线装箱场景，首先探讨提出的装箱算法在预览货物数量p和箱子数量b这两个关键环境超参数变化下的表现. 在p ∈ {1，3，5，10}以及b ∈ {1，2，3}的所有组合情境下进行了实验，平均装箱空间利用率，平均装入货物数量以及空间利用率方差的实验结果如表2所示，其中方差的单位为 10⁻⁴ .

表2不同环境超参数下的实验结果

Table2Results for different environmental hyperparameters

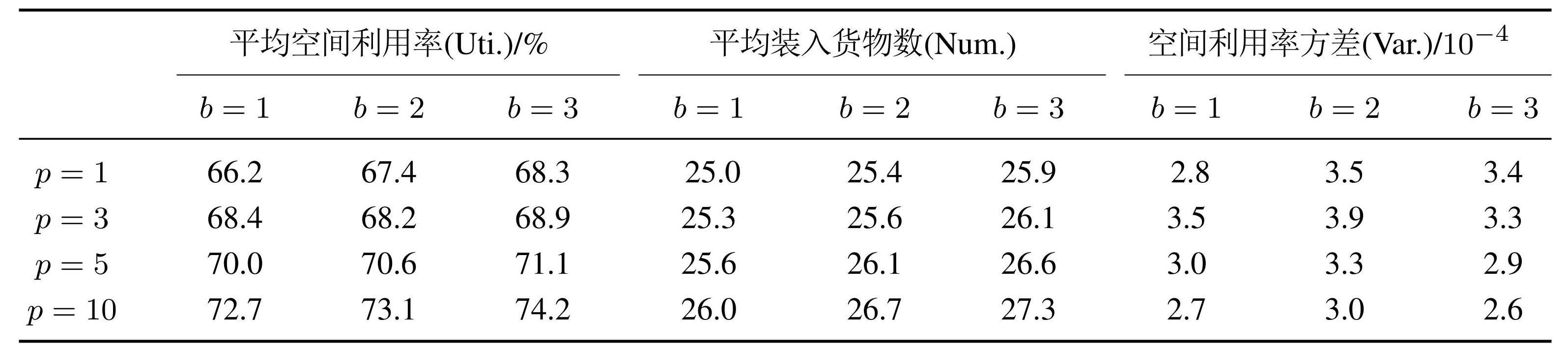
从实验结果中可以观察到，随着p和b的增大，装箱算法的空间利用率和装入货物数量均有所提高，表明这两个环境超参数在一定程度上决定了装箱算法的性能瓶颈. 特别地，装箱空间利用率的方差呈现先上升后下降的趋势，这一现象表明，随着强化学习智能体数量的增加，强化学习算法的训练过程变得更加不稳定. 实验中还发现，在多智能体的情形下，算法相比单智能体需要与环境交互更多的步骤才能收敛. 然而，随着p和b的进一步增大，装箱问题的解空间得到扩展，在线情境下原本无解的装箱流程终止状态可能变为有解，平均空间利用率至多提升8%，平均装入货物数至多增加2.3. 总体而言，针对本文研究的多箱体半在线装箱场景，随着箱子数量和可选择货物数量的增加，本文提出的多智能体强化学习装箱算法的训练难度提高了，但也能获得优秀的性能指标.

5.3 对比实验与泛化能力实验

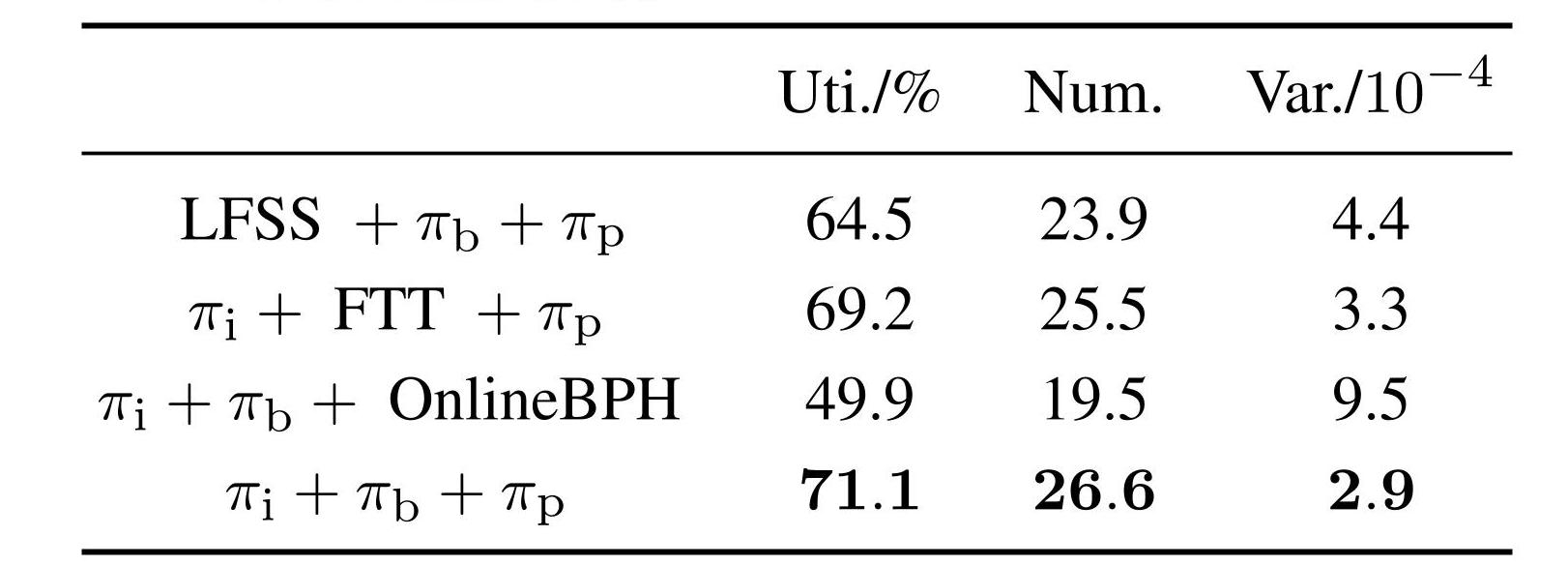
将提出算法中的3个强化学习策略（货物选择策略 π_i，箱子选择策略π_b，位置规划策略π_p）分别替换为相应的启发式方法（分别以LFSS ^[14]，FTT ^[15]，OnlineBPH ^[9] 为例），在环境超参p = 5，b = 3的情形下进行了对比实验，实验结果如表3所示. 容易看出将3个强化学习策略分别替换为启发式策略后，装箱算法性能均出现一定程度的降低，其中替换π_p导致的性能下降最显著，但仍能有效解决装箱问题. 这表明，本文提出的算法在非端到端的决策场景下仍有一定灵活性，可以根据实际问题需要替换对应决策模块. 然而，尽管启发式方法在某些特定情境下能够提供合理的解，但本文提出的多智能体合作强化学习方法在动态决策和适应性优化方面，尤其在复杂的多箱体半在线装箱任务中，具有一定的优势.

表3启发式方法替换强化学习策略对比实验结果

Table3Comparative results of replacing RL policies with heuristics

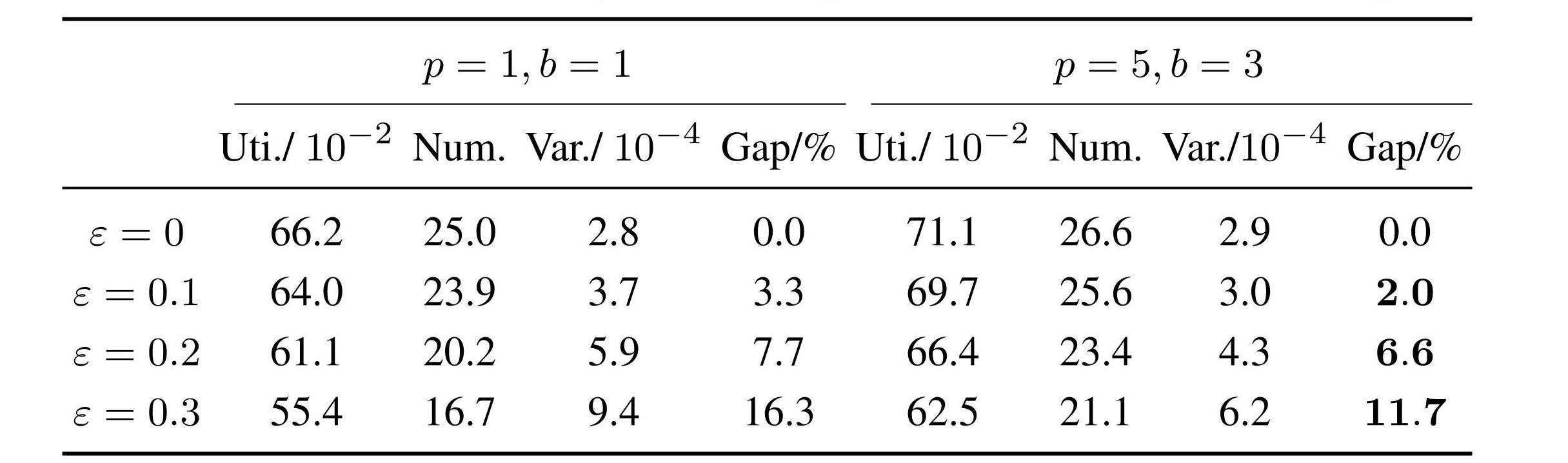
此外，为了探究所提算法在面对服从未知分布的货物尺寸时的泛化能力，在构建验证集装箱问题实例时，以概率ε = {0，0.1，0.2，0.3}从预设分布之外采样货物尺寸（例如随机修改货物某一条边的长度）. 在未经增量训练或重新训练的前提下，直接在验证集装箱问题实例上测试了原始装箱智能体的性能. 表4展示了在线装箱场景（p = 1，b = 1）与多箱体半在线装箱场景（p = 5，b = 3）下的算法性能对比结果，其中Gap 表示与ε = 0时相比空间利用率（Uti.）的相对差距. 从中可以看出，本文提出的多智能体装箱算法在多箱子的半在线复杂装箱场景下，能够获得更好的装箱性能指标，由分布外货物尺寸引起的装箱性能指标下降也得到了抑制. 这一结果从侧面验证了本文提出的装箱问题求解算法在应对实际装箱系统中观测到的货物尺寸多样性时，表现出了更强的鲁棒性和适应性.

表4处理分布外大物体的泛化能力

Table4Generalization ability for dealing with out-of-distribution big items

6 结论

针对涉及箱子选择和货物预览选择的多箱体半在线装箱问题，本文提出了一种创新的多智能体分层深度强化学习框架，合作地完成箱子选择，货物选择及摆放位置规划等环节的决策任务. 在不同设置下的实验结果表明: 1）装箱问题的复杂度随箱子数量和可选择货物数量的增加而提升，多智能体的分层决策框架在多个测试场景中展现出了良好的三维装箱问题求解性能，不仅提高了装箱空间利用率和装入货物数量，还减少了空间利用率的方差，显示出了一定的泛化能力和适应性; 2）多智能体强化学习装箱算法既能端到端地进行装箱决策，也能让神经网络与启发式规则进行协同，以适应特定场景. 与启发式方法相比，多智能体合作强化学习方法在动态决策和适应性优化方面都具有一定优势; 3）多智能体强化学习的装箱算法在面对未知分布的货物尺寸时，仍能保持较好的装箱性能，在应对货物尺寸的多样性与货物尺寸观测噪声时具有一定的鲁棒性.

图1多箱体Semi-online3D BPP场景示意图

Fig.1Multi-bin semi-online packing scenario

下载: 全尺寸图片

图2奖励与终止信号计算流程图

Fig.2The flowchart of calculating reward and terminal signal

下载: 全尺寸图片

图3神经网络模型结构示意图

Fig.3Neural network structure

下载: 全尺寸图片

图4单步装箱中的分层合作决策流程

Fig.4The hierarchical collaborative decision process in one packing step

下载: 全尺寸图片

图5利用EMS启发式方法生成候选摆放位置

Fig.5Generating placement candidates with EMS heuristic

下载: 全尺寸图片

图6Rainbow算法流程示意图

Fig.6Flowchart of the Rainbow algorithm

下载: 全尺寸图片

表1实验超参数

Table1Hyperparameters in our experiments

下载: 全尺寸图片

表2不同环境超参数下的实验结果

Table2Results for different environmental hyperparameters

下载: 全尺寸图片

表3启发式方法替换强化学习策略对比实验结果

Table3Comparative results of replacing RL policies with heuristics

下载: 全尺寸图片

表4处理分布外大物体的泛化能力

Table4Generalization ability for dealing with out-of-distribution big items

下载: 全尺寸图片

图1多箱体Semi-online3D BPP场景示意图

Fig.1Multi-bin semi-online packing scenario

图2奖励与终止信号计算流程图

Fig.2The flowchart of calculating reward and terminal signal

图3神经网络模型结构示意图

Fig.3Neural network structure

图4单步装箱中的分层合作决策流程

Fig.4The hierarchical collaborative decision process in one packing step

图5利用EMS启发式方法生成候选摆放位置

Fig.5Generating placement candidates with EMS heuristic

图6Rainbow算法流程示意图

Fig.6Flowchart of the Rainbow algorithm

表1实验超参数

Table1Hyperparameters in our experiments

表2不同环境超参数下的实验结果

Table2Results for different environmental hyperparameters

表3启发式方法替换强化学习策略对比实验结果

Table3Comparative results of replacing RL policies with heuristics

表4处理分布外大物体的泛化能力

Table4Generalization ability for dealing with out-of-distribution big items

图1多箱体Semi-online3D BPP场景示意图

Fig.1Multi-bin semi-online packing scenario

图2奖励与终止信号计算流程图

Fig.2The flowchart of calculating reward and terminal signal

图3神经网络模型结构示意图

Fig.3Neural network structure

图4单步装箱中的分层合作决策流程

Fig.4The hierarchical collaborative decision process in one packing step

图5利用EMS启发式方法生成候选摆放位置

Fig.5Generating placement candidates with EMS heuristic

图6Rainbow算法流程示意图

Fig.6Flowchart of the Rainbow algorithm

表1实验超参数

Table1Hyperparameters in our experiments

表2不同环境超参数下的实验结果

Table2Results for different environmental hyperparameters

表3启发式方法替换强化学习策略对比实验结果

Table3Comparative results of replacing RL policies with heuristics

表4处理分布外大物体的泛化能力

Table4Generalization ability for dealing with out-of-distribution big items

TRESCA G, CAVONE G, CARLI R,et al. Automating bin packing: A layer building matheuristics for cost effective logistics. IEEE Transactions on Automation Science and Engineering,2022,19(3):1599-1613.

LIU Y, JIANG X. Dynamic feedback algorithm based on spatial corner fitness for solving the three-dimensional multiple bin-size bin packing problem. Complex & Intelligent Systems,2024,10(3):4055-4081.

TSEREMOGLOU I, BOMBELLI A, SANTOS B F. A combined forecasting and packing model for air cargo loading: A risk-averse framework. Transportation Research Part E: Logistics & Transportation Review,2022,158:102579.

BORTFELDT A, WASCHER G. Constraints in container loading-a state-of-the-art review. European Journal of Operational Research,2013,229(1):1-20.

COFFMAN E G, CSIRIK J, GALAMBOS G,et al. Bin packing approximation algorithms: Survey and classification. Handbook of combinatorial optimization. New York: Springer,2013:455-531.

SHEN Ni, XIA Jianan, MA Hong,et al. Three-dimensional multiple bin-size bin packing problem with temperature layer and refrigerant loading constraints. Systems Engineering-Theory & Practice,2025,45(2):685-701.(沈倪, 夏佳楠, 马弘, 等. 考虑温层和冷媒装载约束的冷链商品三维多箱型装箱问题研究. 系统工程理论与实践,2025,45(2):685-701.)

LI Xiao. Research on the solution of a 3D packing optimization problem considering robot packing constraints. Beijing: Beijing Jiao Tong University,2022.(李潇. 考虑机器人装箱约束的三维装箱优化问题的求解研究. 北京: 北京交通大学,2022.)

XU Xiangbin, YU Qinfang. Three-dimensional bin packing considering working posture comfort. Industrial Engineering Journal,2024,27(2):37-47.(徐翔斌, 吁琴芳. 考虑作业姿势舒适的三维装箱问题. 工业工程,2024,27(2):37-47.)

HA C T, NGUYEN T T, BUI L T,et al. An online packing heuristic for the three-dimensional container loading problem in dynamic environments and the physical internet. European Conference on the Applications of Evolutionary Computation. Cham: Springer International Publishing,2017:140-155.

ZHAO H, YU Y, XU K. Learning efficient online 3D bin packing on packing configuration trees. International Conference on Learning Representations.2021.

VASWANI A, SHAZEER N, PARMAR N,et al. Attention is all you need. Advances in Neural Information Processing Systems.2017:30.

HONG Y D, KIM Y J, LEE K B. Smart pack: Online autonomous object-packing system using RGB-D sensor data. Sensors,2020,20(16):4448.

HESSEL M, MODAYIL J, VAN HASSELT H,et al. Rainbow: Combining improvements in deep reinforcement learning. Proceedings of the AAAI conference on artificial intelligence,2018,32:1.

GOYAL A, DENG J. Packit: A virtual environment for geometric planning. International Conference on Machine Learning, PMLR,2020:3700-3710.

GOMEZ J C, TERASHIMA-MARIN H. Evolutionary hyperheuristics for tackling bi-objective 2d bin packing problems. Genetic Programming and Evolvable Machines,2018,19:151-181.