System identification with binary-valued observations under both denial-of-service attacks and data tampering attacks: the optimality of attack strategy

Abstract

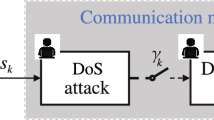
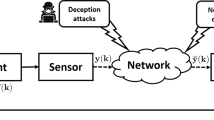
With the development of wireless communication technology, cyber physical systems are applied in various fields such as industrial production and infrastructure, where lots of information exchange brings cyber security threats to the systems. From the perspective of system identification with binary-valued observations, we study the optimal attack problem when the system is subject to both denial of service attacks and data tampering attacks. The packet loss rate and the data tampering rate caused by the attack is given, and the estimation error is derived. Then the optimal attack strategy to maximize the identification error with the least energy is described as a min–max optimization problem with constraints. The explicit expression of the optimal attack strategy is obtained. Simulation examples are presented to verify the effectiveness of the main conclusions.

Appendix: Proof of Lemmas

Proof of Lemma 1

From (11), it is known that $\eta (p_0,p_1,q_0,q_1)$ is increasing with respect to $q_0$. If $\eta (p_0,p_1,q_0,q_1)$ gets the minimum value, then we have $q_0=0$ and

$$\begin{aligned}&\eta (p_0,p_1,q_0,q_1)=\frac{ (1-p_1)(1-q_1)\widetilde{F}}{1-p_0(1- \widetilde{F})- p_1\widetilde{F} }, \end{aligned}$$

which is increasing with respect to $p_0$. Therefore, when $\eta (p_0,$ $p_1,q_0,q_1)$ achieves the minimum value, there is $p_0=0$. At this time, one can get

$$\begin{aligned} \eta (p_0,p_1,q_0,q_1)=\frac{(1-p_1)(1-q_1)\widetilde{F}}{1- p_1\widetilde{F}}. \end{aligned}$$

(21)

According to the constraints (16)–(19) and (21), it follows that

$$\begin{aligned} \eta _{\min }=0\Leftrightarrow \left\{ \begin{array}{l} p_1=1 ~~\text{ or }~~ q_1=1, \\ p_1\widetilde{F} \leqslant \overline{p},\\ q_1(1-p_1)\widetilde{F} \leqslant \overline{q}, \\ \mu _1p_1\widetilde{F}+\mu _2q_1(1-p_1)\widetilde{F}\leqslant \overline{\lambda }, \\ 0 \leqslant p_1,\ q_1 \leqslant 1. \end{array}\right. \end{aligned}$$

(22)

• 1)  If $(\mu _1,\mu _2,\widetilde{F},\overline{p},\overline{q},\overline{\lambda }) \in \mathcal {M}_1$, according to the conditions of the lemma, we know that $p_1$ can be 1. In the case of $p_1=1$, by (22) it can be seen that the constraints (16)–(19) hold, $\forall ~0\leqslant q_1 \leqslant 1$. At this time, we have $\eta _{\min }=0$.

• 2)  If $(\mu _1,\mu _2,\widetilde{F},\overline{p},\overline{q},\overline{\lambda }) \in \mathcal {M}_2$, we know that $q_1$ can be 1. When $q_1=1$, by (22) it can be seen that, for any $p_1$ follows

  $$\begin{aligned} \max \left\{ 0,\frac{\widetilde{F}-\overline{q}}{\widetilde{F}}\right\} =0\leqslant p_1 \leqslant \min \left\{ 1,\frac{\overline{p}}{\widetilde{F}},\frac{\overline{\lambda }-\mu _2\widetilde{F}}{(\mu _1-\mu _2)\widetilde{F}}\right\} , \end{aligned}$$

  the constraints (16)–(19) hold. At this time, we have $\eta _{\min }=0$.

• 3)  If $(\mu _1,\mu _2,\widetilde{F},\overline{p},\overline{q},\overline{\lambda }) \in \mathcal {M}_3$, we know that $q_1$ can be 1. The coming discussion is carried out under $q_1=1$. While $\mu _1<\mu _2$, by (22) it is known that, for any $p_1$ follows

  $$\begin{aligned}&\max \left\{ 0,\frac{\widetilde{F}-\overline{q}}{\widetilde{F}},\frac{\overline{\lambda }-\mu _2\widetilde{F}}{(\mu _1-\mu _2)\widetilde{F}}\right\} \\&\quad =0\leqslant p_1 \leqslant \min \left\{ 1,\frac{\overline{p}}{\widetilde{F}}\right\} =\frac{\overline{p}}{\widetilde{F}}, \end{aligned}$$

  the constraints (16)–(19) hold. At this time, we have $\eta _{\min }=0$. While $\mu _1=\mu _2$, by (22) it can be seen that, for any $p_1$ follows

  $$\begin{aligned} \max \left\{ 0,\frac{\widetilde{F}-\overline{q}}{\widetilde{F}}\right\} =0\leqslant p_1 \leqslant \min \left\{ 1,\frac{\overline{p}}{\widetilde{F}}\right\} =\frac{\overline{p}}{\widetilde{F}}, \end{aligned}$$

  the constraints (16)–(19) hold. At this time, we have $\eta _{\min }=0$. Combing (1)–(3) above, the proof of Lemma 1 is completed. $\square$

Proof of Lemma 2

According to (11), $\eta (p_0,p_1,q_0,q_1)$ is decreasing with respect to $q_1$ in its domain. Therefore, if $\eta (p_0,p_1,q_0,q_1)$ achieves the maximum value, then we have $q_1=0$ and

$$\begin{aligned}&\eta (p_0,p_1,q_0,q_1)=1-\frac{ (1-p_0)(1-q_0)(1-\widetilde{F})}{1-p_0(1- \widetilde{F})- p_1\widetilde{F}}, \end{aligned}$$

which is decreasing with respect to $p_1$. This indicates that, when $\eta (p_0,$ $p_1,q_0,q_1)$ gets the maximum value, there is $p_1=0$. At this point, one can get

$$\begin{aligned}&\eta (p_0,p_1,q_0,q_1)=1-\frac{ (1-p_0)(1-q_0)(1-\widetilde{F})}{1-p_0(1- \widetilde{F})}. \end{aligned}$$

From the above and the constraints (16)–(19), we know that

$$\begin{aligned} \eta _{\max }\!=\!1\!\Leftrightarrow \! \left\{ \begin{array}{l} p_0=1 ~or~ q_0=1, \\ p_0(1-\widetilde{F}) \leqslant \overline{p},\\ q_0(1-p_0)(1-\widetilde{F}) \leqslant \overline{q}, \\ \mu _1p_0(1-\widetilde{F})+\mu _2q_0(1-p_0)(1-\widetilde{F})\leqslant \overline{\lambda }, \\ 0 \leqslant p_0,\ q_0 \leqslant 1. \end{array}\right. \end{aligned}$$

(23)

• 1)  If $(\mu _1,\mu _2,\widetilde{F},\overline{p},\overline{q},\overline{\lambda }) \in \mathcal {M}_4$, according to the conditions of the lemma, we know that $p_0$ can be 1. With $p_0=1$, by (23) it can be seen that the constraints (16)–(19) hold, $\forall ~0\leqslant q_0 \leqslant 1$. At this time, we have $\eta _{\max }=1$.

• 2)  If $(\mu _1,\mu _2,\widetilde{F},\overline{p},\overline{q},\overline{\lambda }) \in \mathcal {M}_5$, it is known that $q_0$ can be 1. When $q_0=1$, from (23) one can have that the constraints (16)–(19) hold with $\max \left\{ 0,\frac{1-\widetilde{F}-\overline{q}}{1-\widetilde{F}}\right\} =0\leqslant p_0 \leqslant \min \left\{ 1,\frac{\overline{p}}{1-\widetilde{F}},\right.$ $\left. \frac{\overline{\lambda }-\mu _2(1-\widetilde{F})}{(\mu _1-\mu _2)(1-\widetilde{F})}\right\} .$ At this time, we have $\eta _{\max }=1$.

• 3)  If $(\mu _1,\mu _2,\widetilde{F},\overline{p},\overline{q},\overline{\lambda }) \in \mathcal {M}_6$, we know that $q_0$ can be 1. The next focuses on the case of $q_0=1$. While $\mu _1<\mu _2$, by (23) it can be seen that the constraints (16)–(19) hold with $\max \left\{ 0,\frac{1-\widetilde{F}-\overline{q}}{1-\widetilde{F}},\frac{\overline{\lambda }-\mu _2(1-\widetilde{F})}{(\mu _1-\mu _2)(1-\widetilde{F})}\right\} =0\leqslant p_0 \leqslant \min \left\{ 1,\frac{\overline{p}}{1-\widetilde{F}}\right\}$ $=\frac{\overline{p}}{1-\widetilde{F}}.$ At this time, we have $\eta _{\max }=1$. While $\mu _1=\mu _2$, by (23) it can be seen that the constraints (16)–(19) hold with $\max \left\{ 0,\frac{1-\widetilde{F}-\overline{q}}{1-\widetilde{F}}\right\}$ $=0\leqslant p_0 \leqslant \min \left\{ 1,\frac{\overline{p}}{1-\widetilde{F}}\right\} =\frac{\overline{p}}{1-\widetilde{F}}.$ At this time, we have $\eta _{\max }$ $=1$. By (1)–(3), Lemma 2 is proved.$\square$

Proof of Lemma 3

If $(\mu _1,\mu _2,\widetilde{F},\overline{p},\overline{q},\overline{\lambda }) \in \mathcal {M}_7$, we know that $p_0=q_0=0$ when $\eta$ takes the minimum value according to the proof process of Lemma 1. At this point, we have $\lambda = \mu _1p+\mu _2q=\mu _1p_1\widetilde{F}+\mu _2q_1(1-p_1)\widetilde{F}$, which gives

$$\begin{aligned} q_1=\frac{\lambda -\mu _1p_1\widetilde{F}}{\mu _2(1-p_1)\widetilde{F}}. \end{aligned}$$

(24)

From the above and (16)–(19), one can get

$$\begin{aligned} \max \left\{ 0,\frac{\lambda -\mu _2\overline{q}}{\mu _1\widetilde{F}}\right\} \leqslant p_1 \leqslant \min \left\{ \frac{\overline{p}}{\widetilde{F}},\frac{\overline{\lambda }}{\mu _1\widetilde{F}}\right\} . \end{aligned}$$

(25)

Substituting (24) into (11), we have $\eta \!=\! \frac{(\mu _1-\mu _2)p_1\widetilde{F}\!+\mu _2\widetilde{F}\!-\lambda }{\mu _2(1-p_1\widetilde{F})}\!,$ which is decreasing with respect to $\lambda$. Therefore, $\lambda$ takes the maximum value when $\eta$ takes the minimum value. Assume that the maximum value of $\lambda$ is $\lambda ^*$ under (16)–(19). It follows that $\eta _{\min } = \frac{(\mu _1-\mu _2)p_1\widetilde{F}+\mu _2\widetilde{F}-\lambda ^*}{\mu _2(1-p_1\widetilde{F})},$ Taking the derivative of this on $p_1$, it can be concluded that

$$\begin{aligned} \frac{\mathrm{d}\eta _{\min }}{\mathrm{d}p_1}=\frac{\mu _2\widetilde{F}(\mu _1-\mu _2+\mu _2\widetilde{F}-\lambda ^*)}{\mu _2^2(1-p_1\widetilde{F})^2}. \end{aligned}$$

Therefore, while $\mu _1-\mu _2+\mu _2\widetilde{F}-\lambda ^*\geqslant 0$, $\eta$ is monotonically increasing with respect to $p_1$. In this case, by (25) we have

$$\begin{aligned} p_1 = \max \left\{ 0,\frac{\lambda ^*-\mu _2\overline{q}}{\mu _1\widetilde{F}}\right\} , \end{aligned}$$

(26)

when $\eta$ takes the minimum value. While $\mu _1-\mu _2+\mu _2\widetilde{F}-\lambda ^*<0$, $\eta$ is monotonically decreasing with respect to $p_1$. In this case, by (25) again we have

$$\begin{aligned} p_1 = \min \left\{ \frac{\overline{p}}{\widetilde{F}},\frac{\overline{\lambda }}{\mu _1\widetilde{F}}\right\} , \end{aligned}$$

(27)

when $\eta$ takes the minimum value.

• 1)  If $\overline{\lambda }\geqslant \mu _1\overline{p}+\mu _2\overline{q}$, one can get $\lambda =\mu _1p+\mu _2q\leqslant \mu _1\overline{p}+\mu _2\overline{q}=\lambda ^*\leqslant \overline{\lambda }.$ Noticing that $\frac{\lambda ^*-\mu _2\overline{q}}{\mu _1\widetilde{F}}=\frac{\overline{p}}{\widetilde{F}}$ when $\lambda ^*=\mu _1\overline{p}+\mu _2\overline{q}$. Therefore, if $\eta$ takes the minimum value, by (27) we have $p_1 = \frac{\overline{p}}{\widetilde{F}},~q_1=\frac{\overline{q}}{\widetilde{F}-\overline{p}},$ and $\eta _{\min }=\frac{\widetilde{F}-\overline{p}-\overline{q}}{1-\overline{p}}.$

• 2)  If $\max \{\mu _1\overline{p},\mu _1-\mu _2+\mu _2\widetilde{F}\}\leqslant \overline{\lambda }< \mu _1\overline{p}+\mu _2\overline{q}$, we have $\lambda =\mu _1p+\mu _2q\leqslant \overline{\lambda }=\lambda ^*< \mu _1\overline{p}+\mu _2\overline{q},$ that is, $\mu _1-\mu _2+\mu _2\widetilde{F}-\lambda ^*=\mu _1-\mu _2+\mu _2\widetilde{F}-\overline{\lambda }\leqslant 0$. In consequence, if $\eta$ takes the minimum value, from (27) we can find that $p_1 =\frac{\overline{p}}{\widetilde{F}},~q_1 = \frac{\overline{\lambda }-\mu _1\overline{p}}{\mu _2(\widetilde{F}-\overline{p})},$ and $\eta _{\min }=\frac{(\mu _1-\mu _2)\overline{p}+\mu _2\widetilde{F}-\overline{\lambda }}{\mu _2(1-\overline{p})}.$

• 3)  If $\mu _2\overline{q} \leqslant \overline{\lambda }< \min \{\mu _1\overline{p}+\mu _2\overline{q},\mu _1-\mu _2+\mu _2\widetilde{F}\}$, then it can be seen that $\lambda =\mu _1p+\mu _2q\leqslant \overline{\lambda }=\lambda ^*< \mu _1\overline{p}+\mu _2\overline{q},$ that is, $\mu _1-\mu _2+\mu _2\widetilde{F}-\lambda ^*=\mu _1-\mu _2+\mu _2\widetilde{F}-\overline{\lambda }\geqslant 0$. As a result, if $\eta$ takes the minimum value, together with (26) we have $p_1 =\frac{\overline{\lambda }-\mu _2\overline{q}}{\mu _1\widetilde{F}}$, $q_1 = \frac{\mu _1\overline{q}}{\mu _1\widetilde{F}+\mu _2\overline{q}-\overline{\lambda }},$ and $\eta _{\min }=\frac{\mu _1\widetilde{F}+(\mu _2-\mu _1)\overline{q}-\overline{\lambda }}{\mu _1+\mu _2\overline{q}-\overline{\lambda }}.$

• 4)  If $\mu _1-\mu _2+\mu _2\widetilde{F}\leqslant \overline{\lambda }<\mu _1\overline{p}$, it follows $\lambda =\mu _1p+\mu _2q\leqslant \overline{\lambda }=\lambda ^*< \mu _1\overline{p},$ that is, $\mu _1-\mu _2+\mu _2\widetilde{F}-\lambda ^*=\mu _1-\mu _2+\mu _2\widetilde{F}-\overline{\lambda }< 0$. Therefore, if $\eta$ takes the minimum value, by (27) one can know $p_1 =\frac{\overline{\lambda }}{\mu _1\widetilde{F}},~q_1 = 0,$ and $\eta _{\min }=\frac{\mu _1\widetilde{F}-\overline{\lambda }}{\mu _1-\overline{\lambda }}.$

• 5)  If $\overline{\lambda }<\min \{\mu _2\overline{q},\mu _1-\mu _2+\mu _2\widetilde{F}\}$, one can get $\lambda =\mu _1p+\mu _2q\leqslant \overline{\lambda }=\lambda ^*< \mu _2\overline{q},$ that is, $\mu _1-\mu _2+\mu _2\widetilde{F}-\lambda ^*=\mu _1-\mu _2+\mu _2\widetilde{F}-\overline{\lambda }\geqslant 0$. If $\eta$ takes the minimum value, from (26) we have $p_1 =0,~q_1 = \frac{\overline{\lambda }}{\mu _2\widetilde{F}},$ and $\eta _{\min }=\widetilde{F}-\frac{\overline{\lambda }}{\mu _2}.$

Above completes the proof of Lemma 3. $\square$

Proof of Lemma 4

If $(\mu _1,\mu _2,\widetilde{F},\overline{p},\overline{q},\overline{\lambda }) \in \mathcal {M}_7$, we know that $p_1=q_1=0$ when $\eta$ takes the maximum value by the proof process of Lemma 2. Hence, it follows that $\lambda = \mu _1p+\mu _2q=\mu _1p_0(1-\widetilde{F})+$ $\mu _2q_0(1-p_0)(1-\widetilde{F})$, that is,

$$\begin{aligned} q_0=\frac{\lambda -\mu _1p_0(1-\widetilde{F})}{\mu _2(1-p_0)(1-\widetilde{F})}. \end{aligned}$$

(28)

From the above and (16)–(19), one can get

$$\begin{aligned} \max \left\{ 0,\frac{\lambda -\mu _2\overline{q}}{\mu _1(1-\widetilde{F})}\right\} \leqslant p_0 \leqslant \min \left\{ \frac{\overline{p}}{1-\widetilde{F}},\frac{\overline{\lambda }}{\mu _1(1-\widetilde{F})}\right\} . \end{aligned}$$

(29)

Substituting (28) into (11), we get

$$\begin{aligned} \eta =1- \frac{(\mu _1-\mu _2)p_0(1-\widetilde{F})+\mu _2(1-\widetilde{F})-\lambda }{\mu _2(1-p_0(1-\widetilde{F}))}, \end{aligned}$$

which is increasing with respect to $\lambda$. Therefore, $\lambda$ takes the maximum value when $\eta$ takes the maximum value, which implies that

$$\begin{aligned} \eta _{\max } = 1- \frac{(\mu _1-\mu _2)p_0(1-\widetilde{F})+\mu _2(1-\widetilde{F})-\lambda ^*}{\mu _2(1-p_0(1-\widetilde{F}))}, \end{aligned}$$

where $\lambda ^*$ is the one in the proof of Lemma 3. Taking the derivative of the above on $p_0$ yields that

$$\begin{aligned} \frac{\mathrm{d}\eta _{\max }}{\mathrm{d}p_0}=-\frac{\mu _2(1-\widetilde{F})(\mu _1-\mu _2\widetilde{F}-\lambda ^*)}{\mu _2^2(1-p_0(1-\widetilde{F}))^2}. \end{aligned}$$

As a result, while $\mu _1-\mu _2\widetilde{F}-\lambda ^*\geqslant 0$, it is known that $\eta$ is monotonically decreasing with respect to $p_0$. In this case, by (29) we have

$$\begin{aligned} p_0 = \max \left\{ 0,\frac{\lambda ^*-\mu _2\overline{q}}{\mu _1(1-\widetilde{F})}\right\} , \end{aligned}$$

(30)

when $\eta$ takes the maximum value. While $\mu _1-\mu _2\widetilde{F}-\lambda ^*<0$, $\eta$ is monotonically increasing with respect to $p_0$. In this case, we have

$$\begin{aligned} p_0 = \min \left\{ \frac{\overline{p}}{1-\widetilde{F}},\frac{\overline{\lambda }}{\mu _1(1-\widetilde{F})}\right\} , \end{aligned}$$

(31)

when $\eta$ takes the maximum value.

• 1)  If $\overline{\lambda }\geqslant \mu _1\overline{p}+\mu _2\overline{q}$, then we know $\lambda =\mu _1p+\mu _2q\leqslant \mu _1\overline{p}+\mu _2\overline{q}=\lambda ^*\leqslant \overline{\lambda }.$ Noticing that $\frac{\lambda ^*-\mu _2\overline{q}}{\mu _1(1-\widetilde{F})}=\frac{\overline{p}}{1-\widetilde{F}}$ when $\lambda ^*=\mu _1\overline{p}+\mu _2\overline{q}$. Therefore, if $\eta$ takes the maximum value, then by (31) we have $p_0 = \frac{\overline{p}}{1-\widetilde{F}},~q_0=\frac{\overline{q}}{1-\widetilde{F}-\overline{p}},$ and $\eta _{\max }=\frac{\widetilde{F}+\overline{q}}{1-\overline{p}}.$

• 2)  If $\max \{\mu _1\overline{p},\mu _1-\mu _2\widetilde{F}\}\leqslant \overline{\lambda }< \mu _1\overline{p}+\mu _2\overline{q}$, it follows that $\lambda =\mu _1p+\mu _2q\leqslant \overline{\lambda }=\lambda ^*< \mu _1\overline{p}+\mu _2\overline{q},$ that is, $\mu _1-\mu _2\widetilde{F}-\lambda ^*=\mu _1-\mu _2\widetilde{F}-\overline{\lambda }\leqslant 0$. If $\eta$ takes the maximum value, from (31) it can be seen that $p_0 =\frac{\overline{p}}{1-\widetilde{F}},~q_0 = \frac{\overline{\lambda }-\mu _1\overline{p}}{\mu _2(1-\widetilde{F}-\overline{p})},$ and $\eta _{\max }=\frac{\mu _2\widetilde{F}-\mu _1\overline{p}+\overline{\lambda }}{\mu _2(1-\overline{p})}.$

• 3)  If $\mu _2\overline{q} \leqslant \overline{\lambda }< \min \{\mu _1\overline{p}+\mu _2\overline{q},\mu _1-\mu _2\widetilde{F}\}$, we have $\lambda =\mu _1p+\mu _2q\leqslant \overline{\lambda }=\lambda ^*< \mu _1\overline{p}+\mu _2\overline{q},$ which indicates $\mu _1-\mu _2\widetilde{F}-\lambda ^*=\mu _1-\mu _2\widetilde{F}-\overline{\lambda }\geqslant 0$. If $\eta$ takes the maximum value, by (30) one can have $p_0 =\frac{\overline{\lambda }-\mu _2\overline{q}}{\mu _1(1-\widetilde{F})},~q_0 = \frac{\mu _1\overline{q}}{\mu _1(1-\widetilde{F})+\mu _2\overline{q}-\overline{\lambda }},$ and $\eta _{\max }=\frac{\mu _1(\widetilde{F}+\overline{q})}{\mu _1+\mu _2\overline{q}-\overline{\lambda }}.$

• 4)  If $\mu _1-\mu _2\widetilde{F}\leqslant \overline{\lambda }<\mu _1\overline{p}$, it follows that $\lambda =\mu _1p+\mu _2q\leqslant \overline{\lambda }=\lambda ^*< \mu _1\overline{p},$ that is, $\mu _1-\mu _2\widetilde{F}-\lambda ^*=\mu _1-\mu _2\widetilde{F}-\overline{\lambda }< 0$. If $\eta$ takes the maximum value, according to (31) we have $p_0 =\frac{\overline{\lambda }}{\mu _1(1-\widetilde{F})},~q_0 = 0,$ and $\eta _{\max }=\frac{\mu _1\widetilde{F}}{\mu _1-\overline{\lambda }}.$

• 5)  If $\overline{\lambda }<\min \{\mu _2\overline{q},\mu _1-\mu _2\widetilde{F}\}$, one can get $\lambda =\mu _1p+\mu _2q\leqslant \overline{\lambda }=\lambda ^*< \mu _2\overline{q},$ that is, $\mu _1-\mu _2\widetilde{F}-\lambda ^*=\mu _1-\mu _2\widetilde{F}-\overline{\lambda }\geqslant 0$. If $\eta$ takes the maximum value, by (31) we have $p_0 =0,~q_0 = \frac{\overline{\lambda }}{\mu _2(1-\widetilde{F})},$ and $\eta _{\max }=\widetilde{F}+\frac{\overline{\lambda }}{\mu _2}.$

Based on the above, Lemma 4 is proved. $\square$